Exercise 2.8: Huffman Application for a Markov Source

Binary symmetric Markov source

We consider the symmetric Markov source according to the graph, which is completely given by the single parameter

$$q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}).$$

The given source symbol sequences apply to the conditional probabilities $q = 0.2$ and $q = 0.8$, respectively.
In subtask (1) it has to be clarified which symbol sequence – the red or the blue one – was generated with $q = 0.2$ and which with $q = 0.8$ .

The properties of Markov sources are described in detail in the chapter Discrete Sources with Memory. Due to the symmetry assumed here with regard to the binary symbols $\rm X$ and $\rm Y$, some serious simplifications result, as is derived in Exercise 1.5Z:

The symbols $\rm X$ and $\rm Y$ are equally probable, that is, $p_{\rm X} = p_{\rm Y} = 0.5$ holds.
Thus the first entropy approximation is $H_1 = 1\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}. $
The entropy of the Markov source for $q = 0.2$ as well as for $q = 0.8$ results in

$$H = q \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{q} + (1-q) \cdot {\rm log_2}\hspace{0.15cm}\frac{1}{1-q} = 0.722\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm}.$$

For Markov sources, all entropy approximations $H_k$ with order $k \ge 2$ are determined by $H_1$ and $H = H_{k \to \infty}$:

$$H_k = {1}/{k}\cdot \big [ H_1 + H \big ] \hspace{0.05cm}.$$

The following numerical values again apply equally to $q = 0.2$ and $q = 0.8$ :

$$H_2 = {1}/{2}\cdot \big [ H_1 + H \big ] = 0.861\,\,{\rm bit/source\hspace{0.15cm}symbol}\hspace{0.05cm},$$

$$H_3 = {1}/{3} \cdot \big [ H_1 + 2H \big ] = 0.815\,\,{\rm bit/source\hspace{0.15cmsymbol}\hspace{0.05cm}.$$

In this exercise, the Huffman algorithm is to be applied to $k$–tuples, where we restrict ourselves to $k = 2$ and $k = 3$.

Hints:

The exercise belongs to the chapter Entropy Coding according to Huffman.
In particular, reference is made to the page Application of Huffman coding to $k$-tuples.
Useful information can also be found in the specification sheets for Exercise 2.7 and Exercise 2.7Z.
To check your results, please refer to the interaction module Huffman and Shannon–Fano––coding.

Questions

Solution

(1) Correct is the solution suggestion 2:

In the blue source symbol sequence 2 one recognizes much less symbol changes than in the red sequence.
The symbol sequence 2 was generated with the parameter $q = {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.8$ and the red symbol sequence 1 with $q = 0.2$.

(2) Answers 2 and 3 are correct.:

Since here the source symbols $\rm X$ and $\rm Y$ were assumed to be equally probable, the direct application of Huffman makes no sense.
In contrast, one can use the inner statistical bonds of the Markov source for data compression if one forms $k$–tuples $(k ≥ 2)$.
The larger $k$ is, the more the mean codeword length $L_{\rm M}$ approaches the entropy $H$.

(3) The symbol probabilities are $p_{\rm X} = p_{\rm Y} = 0.5$, which gives us for the two-tuples.:

$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XX}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot q = 0.5 \cdot 0.8 \hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm},$$

$$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XY}) = p_{\rm X} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm X}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$

$$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YX}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm X}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot (1-q)= 0.5 \cdot 0.2 \hspace{0.15cm}\underline{ = 0.1} \hspace{0.05cm},$$

$$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm YY}) = p_{\rm Y} \cdot {\rm Pr}(\boldsymbol{\rm Y}\hspace{0.05cm}|\hspace{0.05cm}\boldsymbol{\rm Y}) = 0.5 \cdot q = 0.5 \cdot 0.8\hspace{0.15cm}\underline{ = 0.4} \hspace{0.05cm}.$$

For Huffman coding for $k = 2$

(4) Opposite screen capture of the (earlier) SWF program Shannon–Fano– and Huffman–coding shows the construction of the Huffman code for $k = 2$ with the probabilities just calculated.

Thus, the mean codeword length is:

$$L_{\rm M}\hspace{0.01cm}' = 0.4 \cdot 1 + 0.4 \cdot 2 + (0.1 + 0.1) \cdot 3 = 1.8\,\,{\rm bit/two-tuple}$$

$$\Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{2}\hspace{0.15cm}\underline{ = 0.9\,{\rm bit/source\:symbol}}\hspace{0.05cm}.$$

(5) Correct is the suggested solution 2:

According to the source coding theorem $L_{\rm M} ≥ H$ holds.
However, if we apply Huffman coding and disregard ties between non-adjacent symbols $(k = 2)$, the lower bound of the codeword length is not $H = 0.722$, but $H_2 = 0.861$ (the addition bit/source symbol is omitted for the rest of the task).
The result of subtask (4) was $L_{\rm M} = 0.9.$
If an asymmetric Markov chain were present and in such a way that for the probabilities $p_{\rm A}$, ... , $p_{\rm D}$ the values $50\%$, $25\%$ and twice $12.5\%$ would result, then one would come to the average code word length $L_{\rm M} = 0.875$.
How the exact parameters of this asymmetrical Markov source look, however, is not known even to the task creator (G. Söder).
Nor how the value $0.875$ could be reduced to $0.861$ . In any case, the Huffman algorithm is unsuitable for this.

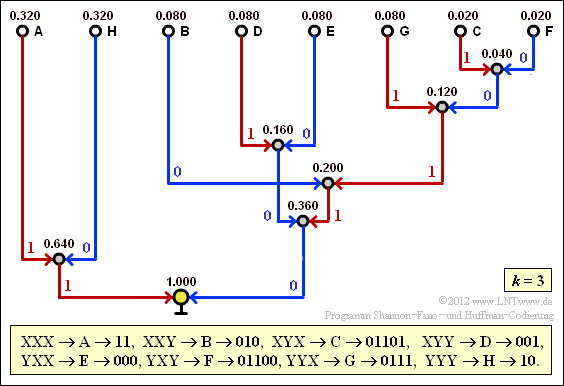
(6) With $q = 0.8$ and $1 - q = 0.2$ we get:

$$p_{\rm A} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXX}) = 0.5 \cdot q^2 \hspace{0.15cm}\underline{ = 0.32} = p_{\rm H} = {\rm Pr}(\boldsymbol{\rm YYY})\hspace{0.05cm},$$

$$p_{\rm B} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XXY}) = 0.5 \cdot q \cdot (1-q) \hspace{0.15cm}\underline{ = 0.08}= p_{\rm G} = {\rm Pr}(\boldsymbol{\rm YYX}) \hspace{0.05cm},$$

$$p_{\rm C} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYX}) = 0.5 \cdot (1-q)^2\hspace{0.15cm}\underline{ = 0.02} = p_{\rm F}= {\rm Pr}(\boldsymbol{\rm YXY}) \hspace{0.05cm},$$

$$p_{\rm D} \hspace{0.2cm} = \hspace{0.2cm} {\rm Pr}(\boldsymbol{\rm XYY}) = 0.5 \cdot (1-q) \cdot q \hspace{0.15cm}\underline{ = 0.08} = p_{\rm E} = {\rm Pr}(\boldsymbol{\rm YXX})\hspace{0.05cm}.$$

(7) The screen capture of the of the (earlier) SWF program Shannon–Fano– and Huffman–coding coding illustrates the constellation of the Huffman code for $k = 3$. This gives us for the mean codeword length:

$$L_{\rm M}\hspace{0.01cm}' = 0.64 \cdot 2 + 0.24 \cdot 3 + 0.04 \cdot 5 = 2.52\,\,{\rm bit/three tupel}\hspace{0.3cm} \Rightarrow\hspace{0.3cm}L_{\rm M} = {L_{\rm M}\hspace{0.01cm}'}/{3}\hspace{0.15cm}\underline{ = 0.84\,{\rm bit/source\:symbol}}\hspace{0.05cm}.$$

On the Huffman coding for $k = 3$

One can see the improvement over subtask (4).
The bound $k = 2$ valid for $H_2 = 0.861$ is now undercut by the mean codeword length $L_{\rm M}$ .
The new bound for $k = 3$ is $H_3 = 0.815$.
However, to reach the source entropy $H = 0.722$ (or better: to come close to this final value up to an $ε$ ), one would have to form infinitely long tuples $(k → ∞)$.

	$L_{\rm M} \ge H_1 = 1.000$ $\ \rm bit/source\:symbol$
	$L_{\rm M} \ge H_2 \approx 0.861$ $\ \rm bit/source\:symbol$
	$L_{\rm M} \ge H_3 \approx 0.815$ $\ \rm bit/source\:symbol$
	$L_{\rm M} \ge H_{k \to \infty} \approx 0.722$ $\ \rm bit/source\:symbol$
	$L_{\rm M} \ge 0.5$ $\ \rm bit/source\:symbol$

	the red source symbol sequence 1,
	the blue source symbol sequence 2.

	The direct application of Huffman is also useful here.
	Huffman makes sense when forming two-tuples $(k = 2)$ .
	Huffman makes sense when forming tuples of three $(k = 3)$ .