Exercise 2.11Z: Arithmetic Coding once again
Here we consider arithmetic coding $(\rm AC)$. All necessary information about this type of entropy coding can be found in Exercise 2.11.
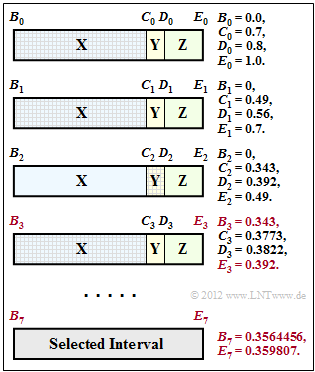
The graph is also the result of Exercise 2.11. The numerical values for coding steps 3 and 7 that are important for the current task are highlighted in colour:
- The interval for $N= 3$ $($symbol sequence $\rm XXY)$ starts at $B_3 = 0.343$ and goes up to $E_3 = 0.392$.
- The interval limits for $N= 7$ $($symbol sequence $\rm XXYXXXZ)$ are $B_7 = 0.3564456$ and $E_7 =0.359807$.
This task is only about assigning binary sequences to the selected intervals. Procedure:
- The interval $I$ is determined by the beginning $B$, the end $E$, the interval width ${\it \Delta} = E-B$ as well as the interval centre $M = (B+E)/2$.
- The interval $I$ is characterised by the binary representation (with limited resolution) of any real number value $r \in I$. For example, one chooses $r \approx M$.
- The required number of bits results from the interval width according to the following equation (the open square brackets mean "round up"):
- $$N_{\rm bits} = \left\lceil{\rm log_2} \hspace{0.15cm} 1/{\it \Delta} \right\rceil+1\hspace{0.05cm}. $$
For example, for $N_{\rm bits} = 5$ the binary code 01001 stands for the following real-valued number $r$:
- $$r = 0 \cdot 2^{-1}+1 \cdot 2^{-2}+0 \cdot 2^{-3}+0 \cdot 2^{-4}+1 \cdot 2^{-5} = 0.28125 \hspace{0.05cm}. $$
Hints:
- The exercise belongs to the chapter Further source coding methods.
- In particular, reference is made to the page Arithmetic Coding.
- Further information on the topic can also be found in this Wikipedia article.
Questions
Solution
- The interval width is therefore ${\it \Delta}_3 = 0.049$ and thus the following applies with the logarithm to base 2:
- $$N_{\rm bits} = {\rm log_2} \hspace{0.15cm} \left\lceil \frac{1}{0.049}\right\rceil+1\hspace{0.15cm}\underline{= 6} \hspace{0.05cm}.$$
(2) The selected interval results in $I = \big[0.343, \ 0.392\big)$.
- The middle lies at $M_3 = 0.3675$.
- To determine the arithmetic code, we try to reach the centre of the interval as well as possible by using a binary representation.
- Since we do not have a corresponding tool for solving this task at the moment, we assume the following secondary calculations:
- $H_4 = 2^{-2} + 2^{-4} = 0.3125$ ⇒ does not belong to interval $I$.
- $H_5 = H_4 +2^{-5} = 0.34375 \in I$ ⇒ binary representation: 0.01011 ⇒ Code: 01011.
- $H_6 = H_5 +2^{-6} = 0.359375 \in I$ ⇒ binary representation: 0.010111 ⇒ Code: 010111.
- $H_7 = H_6 +2^{-7} = 0.3671875 \in I$ ⇒ binary representation: 0.0101111 ⇒ Code: 0101111.
- $H_{12} = H_7 +2^{-12} = 0.3674316406 \in I$ ⇒ binary representation: 0.010111100001 ⇒ Code: 010111100001.
The corresponding 6–bit code is therefore $\rm AC =$ 010111 ⇒ Correct is solution suggestion 2.
(3) Here, with the beginning $B_7 = 0.3564456$ and the end $E_7 = 0.359807$ the interval width is ${\it \Delta}_7 = 0.0033614$ and thus
- $$N_{\rm bits} = \left\lceil {\rm log_2} \hspace{0.15cm} \frac{1}{0.0033614} \right\rceil + 1\hspace{0.15cm} = \left\lceil {\rm log_2} \hspace{0.15cm} 297.5 \right\rceil + 1\hspace{0.15cm} \underline{= 11} \hspace{0.05cm}.$$
(4) The binary representation of the code 01011100001 results in
- $$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-6}+ 2^{-11} = 0.3598632813 > E_7 \hspace{0.05cm}.$$
- The correct answer is therefore NO. The valid arithmetic code is $\rm AC =$ 01011011101, because of
- $$2^{-2}+ 2^{-4}+ 2^{-5}+ 2^{-7}+ 2^{-8}+ 2^{-9}+ 2^{-11} =0.3579101563 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} B_7 \le 0.3579101563 < E_7.$$
(5) All statements are correct. See also:
- Bodden, E.; Clasen, M.; Kneis, J.: Algebraische Kodierung. Proseminar, Lehrstuhl für Informatik IV, RWTH Aachen, 2002.