Exercise 1.4Z: Everything Rectangular

Periodic rectangular signal and
filter with rectangular impulse response

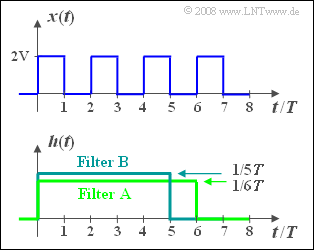
We consider the periodic rectangular signal $x(t)$ , whose periodic duration is $T_0 = 2T$ , according to the sketch above.

This signal has spectral components at the fundamental frequency $f_0 = 1/T_0 = 1/(2T)$ and at all odd multiples thereof, that is, at $3f_0$, $5f_0,$ and so on. In addition, there is a direct component.

For this purpose, we consider two filters $\rm A$ and $\rm B$ each with rectangular impulse response $h_{\rm A}(t)$ with duration $6T$ and $h_{\rm B}(t)$ with duration $5T$, respectively.
The heights of the two impulse responses are such that the areas of the rectangles each add up to $1$ .

Please note:

The exercise belongs to the chapter System Description in Time Domain.
For information on convolution, see the chapter convolution theorem and operation in the book "Signal Representation”.
We also refer you to the interactive applet Zur Verdeutlichung der graphischen Faltung.

Questions

$y_{\rm A}(t = 0) \ =\ $

$\rm V$

$y_{\rm A}(t = T) \ =\ $

$\rm V$

$|H_{\rm A}(f = f_0)| \ =\ $

$y_{\rm B}(t = 0) \ =\ $

$\rm V$

$y_{\rm B}(t = T) \ =\ $

$\rm V$

$|H_{\rm B}(f = f_0)| \ =\ $

$|H_{\rm B}(f = 3f_0)| \ =\ $

Solution

(1) The output signal is the result of the convolution operation between $x(t)$ and $h_{\rm A}(t)$:

$$y_{\rm A}(t) = x (t) * h_{\rm A} (t) = \int_{ - \infty }^{ + \infty } {x ( \tau )} \cdot h_{\rm A} ( {t - \tau } ) \hspace{0.1cm}{\rm d}\tau.$$

Because of the rectangular function and the duration $6T$ this can also be written as follows:

$$y_{\rm A}(t) = \frac{1}{6T}\cdot \int_{t-6T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$

It can be seen that this equation gives the same result $y_{\rm A}(t) \rm \underline{\: = 1V}$ for all $t$ .

(2) The magnitude of the frequency response is $|H_{\rm A}(f)| = |{\rm si}(\pi \cdot f \cdot 6T)|.$ This has zeros at an interval of $1/(6T)$ .

So, there are also zeros at $f_0$, $3f_0$, $5f_0$ etc., respectively.
In particular, $|H_{\rm A}(f = f_0)| \underline{\: = 0}$ holds, too.
From the spectrum $X(f)$ only the direct component $1 \hspace{0.05cm} \rm V$ remains unchanged.
In contrast to this, all other spectral lines in $Y_{\rm A}(f)$ are no longer included.

rechts

(3) Analogous to the subtask (1) for the output signal the following can be recorded:

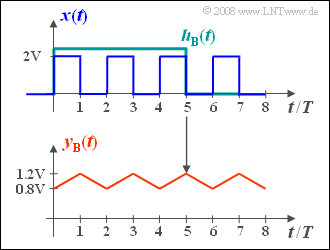
$$y_{\rm B}(t) = \frac{1}{5T}\cdot \int_{t-5T}^{t}x(\tau)\hspace{0.15cm} {\rm d}\tau.$$

This results in a triangular shape fluctuating around the mean $1 \ \rm V$ ⇒ see bottom graph.
Since two rectangles and three gaps each are covered by the integration interval, the following holds for $t = 0, t = 2T,$ etc.:

$$y_{\rm B}(t) = \frac{2\,{\rm V} \cdot 2T }{5T} \hspace{0.15cm}\underline{= 0.8\,{\rm V} =y_{\rm B}(t=0) }.$$

For $t = T,\ 3T, \ 5T, $ etc., there are three rectangles and two gaps each to be considered: One obtains:

$$y_{\rm B}(t) \underline{\: = 1.2 \: {\rm V}=y_{\rm B}(t=T)}.$$

(4) The magnitude function is generally or at frequencies $f = f_0 = 1/(2T)$ and $f = 3f_0$:

$$\begin{align*} |H_{\rm B}(f)| & = |{\rm si}(\pi \cdot f \cdot 5T)|, \\ |H_{\rm B}(f = f_0)| & = |{\rm si}(\pi \frac{5T}{2T})| = |{\rm si}(2.5\pi )| = \frac{1}{2.5 \pi} \hspace{0.15cm}\underline{= 0.127}, \\ |H_{\rm B}(f = 3f_0)| & = |{\rm si}(7.5\pi )| = \frac{1}{7.5 \pi} \hspace{0.15cm}\underline{=0.042}.\end{align*}$$

Interpretation:

The spectral components of the rectangular signal at $f_0, 3f_0,$ etc., although now no longer suppressed, are increasingly attenuated as the frequency increases, in such a way that the rectangular curve is converted into a periodic triangular signal. The direct component $(1 \hspace{0.05cm} \rm V)$ remains unchanged here, too.
Thus, both filters provide the average value of the input signal. For the signal $x(t)$ at hand the filter $\rm A$ is more suitable than the filter $\rm B$for the determination of the mean value, because for the former the length of the impulse response is a multiple of the period $T_0 = 2T$ .
If this condition – as with the filter $\rm B$ – is not fulfilled, an error signal (triangular in this example) is still superimposed on the mean value.