Exercise 3.8: Once more Mutual Information

• Return to book

2D–Functions 
 $P_{ XY }$  und  $P_{ XW }$

We consider the tuple  $Z = (X, Y)$, where the individual components  $X$  and  $Y$  each represent ternary random variables:

$$X = \{ 0 ,\ 1 ,\ 2 \} , \hspace{0.3cm}Y= \{ 0 ,\ 1 ,\ 2 \}.$$

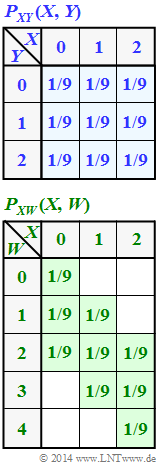
The joint probability function  $P_{ XY }(X, Y)$  of both random variables is given in the upper graph. 

In  Exercise 3.8Z  this constellation is analysed in detail.  One obtains as a result (all data in "bit"):

• $H(X) = H(Y) = \log_2 (3) = 1.585,$
• $H(XY) = \log_2 (9) = 3.170,$
• $I(X, Y) = 0,$
• $H(Z) = H(XZ) = 3.170,$
• $I(X, Z) = 1.585.$

Furthermore, we consider the random variable  $W = \{ 0,\ 1,\ 2,\ 3,\ 4 \}$, whose properties result from the composite probability function  $P_{ XW }(X, W)$  according to the sketch below.  The probabilities are zero in all fields with a white background.

What is sought in the present exercise is the mutual information between

• the random variables  $X$  and  $W$   ⇒   $I(X; W)$,
• the random variables  $Z$  and  $W   ⇒   I(Z; W)$.

Hints:

• The exercise belongs to the chapter  Different entropies of two-dimensional random variables.
• In particular, reference is made to the pages
      Conditional probability and conditional entropy as well as
      Mutual information between two random variables.

Questions

1

How might the variables  $X$,  $Y$  and  $W$  be related?

	$W = X + Y$,
	$W = X - Y + 2$,
	$W = Y - X + 2$.

2

What is the mutual information between the random variables  $X$  and  $W$?

$I(X; W) \ = \ $ $\ \rm bit$

3

What is the mutual information between the random variables  $Z$  and  $W$?

$I(Z; W) \ = \ $ $\ \rm bit$

4

Which of the following statements are true?

	$H(ZW) = H(XW)$  is true.
	$H(W|Z) = 0$  is true.
	$I(Z; W) > I(X; W)$  is true.

Solution

Solution

(1)  Thecorrect solutions are 1 and 2:

• With  $X = \{0,\ 1,\ 2\}$,  $Y = \{0,\ 1,\ 2\}$ ,   $X + Y = \{0,\ 1,\ 2,\ 3,\ 4\}$ holds. 
• The probabilities also agree with the given probability function.
• Checking the other two specifications shows that $W = X – Y + 2$ is also possible, but not $W = Y – X + 2$.

(2)  From the 2D probability function  $P_{ XW }(X, W)$  on the specification page, one obtains for

• the joint entropy:

$$H(XW) = {\rm log}_2 \hspace{0.1cm} (9) = 3.170\ {\rm (bit)} \hspace{0.05cm},$$

• the probability function of the random variable  $W$:

$$P_W(W) = \big [\hspace{0.05cm}1/9\hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm},\hspace{0.15cm} 3/9 \hspace{0.05cm}, \hspace{0.15cm} 2/9\hspace{0.05cm}, \hspace{0.15cm} 1/9\hspace{0.05cm} \big ]\hspace{0.05cm},$$

• the entropy of the random variable $W$:

$$H(W) = 2 \cdot \frac{1}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{1} + 2 \cdot \frac{2}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{2} + \frac{3}{9} \cdot {\rm log}_2 \hspace{0.1cm} \frac{9}{3} {= 2.197\ {\rm (bit)}} \hspace{0.05cm}.$$

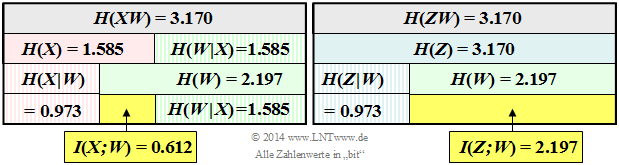
Thus, with  $H(X) = 1.585 \ \rm bit$  (was given), the result for the  Mutual Information:

$$I(X;W) = H(X) + H(W) - H(XW) = 1.585 + 2.197- 3.170\hspace{0.15cm} \underline {= 0.612\ {\rm (bit)}} \hspace{0.05cm}.$$

To calculate the mutual information

The left of the two diagrams illustrates the calculation of the mutual information  $I(X; W)$  between the first component  $X$  and the sum  $W$.

(3)  The second graph shows the joint probability  $P_{ ZW }(⋅)$.  The scheme consists of  $5 · 9 = 45$  fields in contrast to the plot of  $P_{ XW }(⋅)$  on the data page with  $3 · 9 = 27$  fields.

• However, of the  $45$  fields, only nine are also assigned non-zero probabilities.  The following applies to the compound entropy:   $H(ZW) = 3.170\ {\rm (bit)} \hspace{0.05cm}.$
• With the further entropies  $H(Z) = 3.170\ {\rm (bit)}\hspace{0.05cm}$  and  $H(W) = 2.197\ {\rm (bit)}\hspace{0.05cm}$  according  Exercise 3.8Z  or the subquestion  (2)  of this exercise, one obtains for the mutual information:

$$I(Z;W) = H(Z) + H(W) - H(ZW) \hspace{0.15cm} \underline {= 2.197\,{\rm (bit)}} \hspace{0.05cm}.$$

(4)  All three statements are true, as can also be seen from the right-hand side of the two upper diagrams.

We attempt an interpretation of these numerical results:

• The joint probability  $P_{ ZW }(⋅)$ , like  $P_{ XW }(⋅)$ , is composed of nine equally probable elements unequal to 0. It is thus obvious that the compound entropies are also equal   ⇒   $H(ZW) = H(XW) = 3.170 \ \rm (bit)$.
• If I know the tuple  $Z = (X, Y)$ , I naturally also know the sum  $W = X + Y$.  Thus  $H(W|Z) = 0$.
• In contrast,  $H(Z|W) \ne 0$.  Rather,  $H(Z|W) = H(X|W) = 0.973 \ \rm (bit)$.
• The random variable  $W$  thus provides exactly the same information with regard to the tuple  $Z$  as for the individual component  $X$.  This is the verbal interpretation of the statement  $H(Z|W) = H(X|W)$.
• The joint information of  $Z$  and  $W$    ⇒   $I(Z; W)$  is greater than the joint information of  $X$  and  $W$   ⇒   $I(X; W)$, because  $H(W|Z) =0$ , while  $H(W|X)$  is non-zero, namely exactly as great as  $H(X)$ :

$$I(Z;W) = H(W) - H(W|Z) = 2.197 - 0= 2.197\,{\rm (bit)} \hspace{0.05cm},$$

$$I(X;W) = H(W) - H(W|X) = 2.197 - 1.585= 0.612\,{\rm (bit)} \hspace{0.05cm}.$$