Exercise 3.8Z: Tuples from Ternary Random Variables

• Return to book

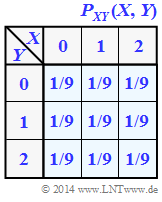
We consider the tuple  $Z = (X, Y)$,  where the individual components  $X$  and  $Y$  each represent ternary random variables   ⇒   symbol set size  $|X| = |Y| = 3$.  The joint probability function  $P_{ XY }(X, Y)$  is sketched on the right.

In this exercise, the following entropies are to be calculated:

• the  "joint entropy"  $H(XY)$  and the  "mutual information"  $I(X; Y)$,
• the  "joint entropy"  $H(XZ)$  and the  "mutual information"  $I(X; Z)$,
• the two  "conditional entropies"  $H(Z|X)$  and  $H(X|Z)$.

Hints:

• The exercise belongs to the chapter  Different entropies of two-dimensional random variables.
• In particular, reference is made to the pages 
      Conditional probability and conditional entropy   as well as
     Mutual information between two random variables.

Questions

1

Calculate the following entropies.

$H(X)\ = \ $ $\ \rm bit$

$H(Y)\ = \ $ $\ \rm bit$

$ H(XY)\ = \ $ $\ \rm bit$

2

What is the mutual information between the random variables  $X$  and  $Y$?

$I(X; Y)\ = \ $ $\ \rm bit$

3

What is the mutual information between the random variables  $X$  and  $Z$?

$I(X; Z)\ = \ $ $\ \rm bit$

4

What conditional entropies exist between  $X$  and  $Z$?

$H(Z|X)\ = \ $ $\ \rm bit$

$ H(X|Z)\ = \ $ $\ \rm bit$

Solution

Solution

(1)  For the random variables  $X =\{0,\ 1,\ 2\}$   ⇒   $|X| = 3$  and  $Y = \{0,\ 1,\ 2\}$   ⇒   $|Y| = 3$  there is a uniform distribution in each case. 

• Thus one obtains for the entropies:

$$H(X) = {\rm log}_2 \hspace{0.1cm} (3) \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}} \hspace{0.05cm},$$

$$H(Y) = {\rm log}_2 \hspace{0.1cm} (3) \hspace{0.15cm}\underline{= 1.585\,{\rm (bit)}}\hspace{0.05cm}.$$

• The 2D random variable  $XY = \{00,\ 01,\ 02,\ 10,\ 11,\ 12,\ 20,\ 21,\ 22\}$   ⇒   $|XY| = |Z| = 9$  also has equal probabilities:

$$p_{ 00 } = p_{ 01 } =\text{...} = p_{ 22 } = 1/9.$$

• From this follows:

$$H(XY) = {\rm log}_2 \hspace{0.1cm} (9) \hspace{0.15cm}\underline{= 3.170\,{\rm (bit)}} \hspace{0.05cm}.$$

(2)  The random variables  $X$  and  $Y$  are statistically independent because of  $P_{ XY }(⋅) = P_X(⋅) · P_Y(⋅)$ .

• From this follows  $I(X, Y)\hspace{0.15cm}\underline{ = 0}$.
• The same result is obtained by the equation  $I(X; Y) = H(X) + H(Y) – H(XY)$.

(3)  If one interprets  $I(X; Z)$  as the remaining uncertainty with regard to the tuple  $Z$,when the first component  $X$  is known, then the following obviously applies

Probability function of the 2D random variable  $XZ$

$$ I(X; Z) = H(Y)\hspace{0.15cm}\underline{ = 1.585 \ \rm bit}.$$

In purely formal terms, this task can also be solved as follows:

• The entropy  $H(Z)$  is equal to the joint entropy  $H(XY) = 3.170 \ \rm bit$.
• The joint probability  $P_{ XZ }(X, Z)$  contains nine elements of probability  $1/9$,  all others are occupied by zeros   ⇒   $H(XZ) = \log_2 (9) = 3.170 \ \rm bit $.
• Thus, the following applies to the mutual information  $($mutual information of the random variables  $X$  and  $Z)$:

$$I(X;Z) = H(X) + H(Z) - H(XZ) = 1.585 + 3.170- 3.170\hspace{0.15cm} \underline {= 1.585\,{\rm (bit)}} \hspace{0.05cm}.$$

Entropies of the 2D random variable  $XZ$

(4)  According to the second graph:

$$H(Z \hspace{-0.1cm}\mid \hspace{-0.1cm} X) = H(XZ) - H(X) = 3.170-1.585\hspace{0.15cm} \underline {=1.585\ {\rm (bit)}} \hspace{0.05cm},$$

$$H(X \hspace{-0.1cm}\mid \hspace{-0.1cm} Z) = H(XZ) - H(Z) = 3.170-3.170\hspace{0.15cm} \underline {=0\ {\rm (bit)}} \hspace{0.05cm}.$$

• $H(Z|X)$  gives the residual uncertainty with respect to the tuple  $Z$ when the first componen  $X$  is known.
• The uncertainty regarding the tuple  $Z$  is $H(Z) = 2 · \log_2 (3) \ \rm bit$.
• When the component  $X$  is known, the uncertainty is halved to  $H(Z|X) = \log_2 (3)\ \rm bit$.
• $H(X|Z)$  gives the remaining uncertainty with respect to component  $X$  when the tuple  $Z = (X, Y)$  is known. 
• This uncertainty is of course zero:   If one knows  $Z$, one also knows  $X$.