Exercise 4.1: PDF, CDF and Probability
To repeat some important basics from the book "Theory of Stochastic Signals" we are dealing with
- the probability density function (PDF),
- the cumulative distribution function (CDF).
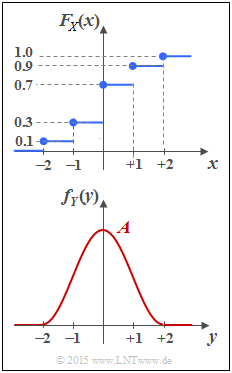
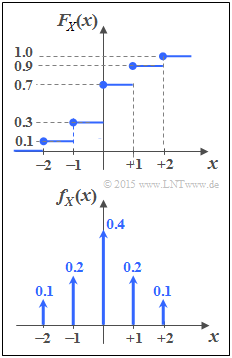
The upper plot shows the distribution function $F_X(x)$ of a discrete value random variable $X$. The corresponding PDF $f_X(x)$ has to be determined in subtask (1) .
The equation
- $$ {\rm Pr}(A < X \le B) = F_X(B) - F_X(A) = \lim_{\varepsilon \hspace{0.05cm}\rightarrow \hspace{0.05cm}0} \int_{A+\varepsilon}^{B+\varepsilon} \hspace{-0.15cm} f_X(x) \hspace{0.1cm}{\rm d}x $$
represents two ways to calculate the probability for the event „The random variable $X$ lies in a given interval” from the CDF and the PDF, respectively.
The lower graph shows the probability density function
- $$ f_Y(y) = \left\{ \begin{array}{c} \hspace{0.1cm}1/2 \cdot \cos^2(\pi/4 \cdot y) \\ \hspace{0.1cm} 0 \\ \end{array} \right.\quad \begin{array}{*{20}c} {\rm{f\ddot{u}r}} \\ {\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{20}l} | y| \le 2, \\ y < -2 \hspace{0.1cm}{\rm und}\hspace{0.1cm}y > +2 \\ \end{array}$$
of a continuous-valued random variable $Y$, which is restricted to the range $|Y| \le 2$ . In principle, the same relationship between PDF, CDF and probabilities exists for the continuous random variable $Y$ as for a discrete random variable. Nevertheless, you will notice some differences in details.
For example, for the continuous random variable $Y$ , the boundary transition can be omitted in the above equation, and we obtain simplified:
- $${\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A) =\int_{A}^{B} \hspace{-0.01cm} f_Y(y) \hspace{0.1cm}{\rm d}y\hspace{0.05cm}.$$
Hints:
- The task belongs to the chapter Differential Entropy.
- Useful hints for solving this problem and further information on continuous-valued random variables can be found in the third chapter "Continuous Random Variables" of the book Theory of Stochastic Signals.
- Given also is the following indefinite integral:
- $$\int \hspace{0.1cm} \cos^2(A \eta) \hspace{0.1cm}{\rm d}\eta = \frac{\eta}{2} + \frac{1}{4A} \cdot \sin(2A \eta).$$
Questions
Solution
(1) Proposed solutions 1 and 2 are correct:
- The cumulative distribution function (CDF) $F_X(x)$ is obtained from the probability density function $f_X(x)$ by integration over the (renamed) random variable in the range from $- \infty$ to $x$.
- The inverse is: given the CDF, obtain the PDF by differentiation.
- The given CDF contains five discontinuity points, which after differentiation lead to five Dirac functions:
- $$f_X(x) = 0.1 \cdot {\rm \delta}( x+2) + 0.2 \cdot {\rm \delta}( x+1) + 0.4 \cdot {\rm \delta}( x) + 0.2 \cdot {\rm \delta}( x-1) + 0.1 \cdot {\rm \delta}( x-2)\hspace{0.05cm}.$$
- The Dirac weights give the occurrence probabilities of the random variable $X = \{-2,\ -1,\ 0,\ +1,\ +2\}$ an,
for example:
- $${\rm Pr}(X = 0) = F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_X(x \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-}) = 0.7 - 0.3 = 0.4\hspace{0.05cm}.$$
- Accordingly, the other probabilities are:
- $${\rm Pr}(X = +1) = {\rm Pr}(X = -1) = 0.2\hspace{0.05cm},\hspace{0.3cm} {\rm Pr}(X = +2) = {\rm Pr}(X = -2) = 0.1\hspace{0.05cm}.$$
(2) From the PDF just calculated, we obtain:
- $${\rm Pr}(X >0) = {\rm Pr}(X = +1) + {\rm Pr}(X = +2) \hspace{0.15cm}\underline {= 0.3}\hspace{0.05cm},$$
- $${\rm Pr}(|X| \le 1) ={\rm Pr}(X = -1) + {\rm Pr}(X = 0) + {\rm Pr}(X = +1) = 0.2 + 0.4 +0.2 \hspace{0.15cm}\underline {= 0.8}\hspace{0.05cm}.$$
The same result is obtained using the distribution function. Here the general equation, which is equally valid for discrete-value and continuous-value random variables, is:
- $${\rm Pr}(A < X \le B) =F_X(B) - F_X(A) \hspace{0.05cm}.$$
- Thus, with $A= 0$ and $B = +2$ we obtain:
- $${\rm Pr}(0 < X \le +2) = {\rm Pr}(X >0)= F_X(+2) - F_X(0) = 1 - 0.7 \hspace{0.15cm}\underline {= 0.3} \hspace{0.05cm}.$$
- Setting $A=-2$ and $B = +1$, we get:
- $${\rm Pr}(-2 < X \le +1) = {\rm Pr}(|X| \le 1)= F_X(+1) - F_X(-2) = 0.9 - 0.1 \hspace{0.15cm}\underline {= 0.8} \hspace{0.05cm}.$$
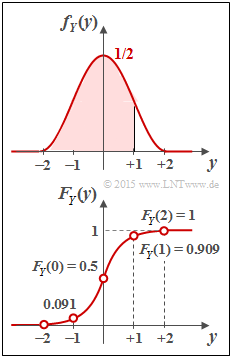
(3) The cumulative distribution function $F_Y(y)$ is obtained from the (renamed) WDF $f_Y(\eta)$ by integrating $- \infty$ to $x$. Due to symmetry, this can be written in the range $0 \le y \le +2$ :
- $$F_Y(y) = \int_{-\infty}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta ={1}/{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{-0.1cm}f_Y(\eta) \hspace{0.1cm}{\rm d}\eta$$
- $$\Rightarrow \hspace{0.3cm}F_Y(y) = \frac{1}{2}+\int_{0}^{\hspace{0.05cm}y} \hspace{0.1cm}\frac{1}{2} \cdot \cos^2({\pi}/{4} \cdot \eta) \hspace{0.1cm}{\rm d}\eta = \frac{1}{2}+\frac{y}{4} + \frac{1}{2\pi} \cdot \sin({\pi}/{2} \cdot y).$$
The equation holds in the entire range $0 \le y \le +2$. The CDF values we are looking for are thus:
- $F_Y(y=0)\hspace{0.15cm}\underline{= 0.5}$ (integral over half the PDF),
- $F_Y(y=1)= 3/4 + 1/(2 \pi)\hspace{0.15cm}\underline{= 0.909}$ (area in red background in the PDF),
- $F_Y(y=2)\hspace{0.15cm}\underline{= 1}$ (integral over the entire PDF).
(4) The probability that the continuous-value random variable $Y$ lies in the range from $-\varepsilon$ to $+\varepsilon$ can be calculated using the given equation as follows:
- $${\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = F_Y(+\varepsilon) - F_Y(-\varepsilon) \hspace{0.05cm}.$$
- It was taken into account that for the continuous random variable $Y$ the "<"sign can be replaced by the "≤" sign without distortion.
- With the boundary transition $\varepsilon \to 0$ , the probability we are looking for is obtained:
- $${\rm Pr}(Y = 0) =\lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm}{\rm Pr}(-\varepsilon \le Y \le +\varepsilon) = \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(+\varepsilon) - \lim_{\varepsilon\hspace{0.05cm}\rightarrow\hspace{0.05cm}0}\hspace{0.1cm} F_Y(-\varepsilon) = F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{+}) - F_Y(y \hspace{0.05cm}\rightarrow\hspace{0.05cm}0^{-})\hspace{0.05cm}.$$
- Since for a continuous random variable the two limits are equal, $\underline{{\rm Pr}(Y = 0) = 0}$.
In general: The probability ${\rm Pr}(Y = y_0)$ that a continuous value random variable $Y$ takes a fixed value $y_0$ is always zero.
(5) Proposed solution 2 is correct:
- Based on the PDF at hand, the result $Y=3$ can be excluded.
- The result $Y=0$ on the other hand is quite possible, although ${\rm Pr}(Y = 0) = 0$ .
- For example, if one performs a random experiment $N \to \infty$ times and obtains the result $Y= 0$ $N_0$ times, then with finite $N_0$ according to the classical definition of probability:
- $${\rm Pr}(Y = 0) = \lim_{N\hspace{0.05cm}\rightarrow\hspace{0.05cm}\infty}\hspace{0.1cm}{N_0}/{N} = 0\hspace{0.05cm}.$$
(6) We again assume the equation $Y$ valid for the continuous random quantity $ {\rm Pr}(A \le Y \le B) = F_Y(B) - F_Y(A)$ :
- With $A = 0$ and $B \to \infty$ $($bzw. $B = 2)$ we obtain:
- $${\rm Pr}( Y > 0) = {\rm Pr}(0 \le Y \le \infty) = {\rm Pr}(0 \le Y \le 2) = F_Y(2) - F_Y(0) \hspace{0.15cm}\underline {= 0.5}\hspace{0.05cm}.$$
- Thus, for the symmetric continuous random variable $Y$ is indeed as expected ${\rm Pr}( Y > 0) = 1/2$.
- Although the discrete value random variable $X$ is also symmetric about $x= 0$ , ${\rm Pr}( X > 0) = 0.3$ was determined in subtask (3) , on the other hand.
- Further, with $A = -1$ and $B = +1$ , one obtains because of $F_Y(-1) = 1- F_Y(+1)$:
- $${\rm Pr}( |Y| \le 1) = {\rm Pr}(-1 \le Y \le +1) = F_Y(+1) - F_Y(-1) = 2 \cdot F_Y(+1) -1 = 2 \cdot 0.909 -1 \hspace{0.15cm}\underline {= 0.818}. $$