Exercise 4.8Z: What does the AWGN Channel Capacity Curve say?

Channel capacity as a function of $10 \cdot \lg (E_{\rm B}/{N_0})$

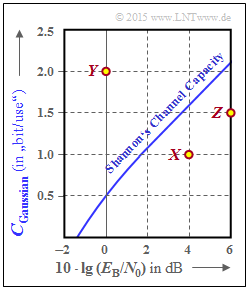
We consider the channel capacity of the AWGN channel as in Exercise 4.8:

$$C_{\rm Gaussian}( E_{\rm B}/{N_0}) = {1}/{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) . $$

The curve is shown on the right with logarithmic abscissa between $-2 \ \rm dB$ and $+6 \ \rm dB$ dargestellt.
The addition of "Gaussian" indicates that a Gaussian distribution was assumed for this curve at the AWGN input.

Three system variants are indicated by dots in the graph:

System $X$: with $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$ and $R = 1$,
System $Y$: with $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ and $R = 2$,
System $Z$: with $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB$ and $R = 1.5$.

In the questions for this exercise, we still use the following terms:

Digital system: Symbol set size $M_X = |X|$ beliebig,
Binary system: Symbol set size $M_X = 2$,
Quaternary system: Symbol set size $M_X = 4$.

Hints:

The exercise belongs to the chapter AWGN channel capacity with discrete value input.
Reference is made in particular to the page The channel capacity $C$ as a function of $E_{\rm B}/{N_0}$.
Since the results are to be given in "bit" ⇒ "log" ⇒ "log₂" is used in the equations.

Questions

Solution

(1) Proposed solutions 1 and 3 are correct:

Since the point $X$ lies to the right of the channel capacity curve $C_\text{Gauß}(E_{\rm B}/{N_0})$ , there is (at least) one message system of rate $R = 1$that provides quasi–error–free transmission with $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$ .
Despite the code rate $R = 1$ , this system includes a channel coding with an infinitely long code, but unfortunately this code is unknown.
However, a binary system of rate $R = 1$ does not allow channel coding.

(2) Only the proposed solution 2 is correct. Here the following statements are valid:

The required $E_{\rm B}/{N_0}$ for the rate $R = 2$ results in

$$(E_{\rm B}/{N_0})_{\rm min} = \frac{2^{2R} - 1} { 2 \cdot R} = \frac{2^4 - 1} { 4 } = 3.75 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 10\cdot {\rm lg} \hspace{0.1cm}(E_{\rm B}/{N_0})_{\rm min} = 15.74\,{\rm dB} \hspace{0.05cm}. $$

The maximum code rate $R_{\rm max}$ for $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ ⇒ $E_{\rm B}/{N_0} = 1$ is calculated as follows:

$$C = R = \frac{1}{2} \cdot {\rm log}_2 \hspace{0.1cm} ( 1 + \frac { 2 \cdot R \cdot E_{\rm B}}{N_0}) \hspace{0.3cm}\Rightarrow \hspace{0.3cm} 2^{2R} - 1 \stackrel{!}{=} 2 R \hspace{0.3cm}\Rightarrow \hspace{0.3cm} R_{\rm max} = 0.5 \hspace{0.05cm}. $$

Both calculations show that the point $Y$ with characteristics $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ and $R = 1$ does not satisfy the channel coding theorem.

(3) With a binary system, the rate $R = 1.5$ can never be realized ⇒ proposed solution 1.

(4) Correct is the proposed solution 2:

The point $Z$ ies to the right of the boundary curve and for the code rate of a quaternary system $R \le 2$ holds.
So the rate $R =1.5$ would be quite realizable with $M_X = 4$ .
The proposed solution 1 is wrong. On the other hand, the second solution suggestion is correct:

The given curve $C_\text{Gauß}(E_{\rm B}/{N_0})$ always assumes a Gaussian distributed input.
For a binary system, a different boundary curve results, namely $C_\text{BPSK} ≤ 1 \ \rm bit/channel use$. $C_\text{Gauß}$ and $C_\text{BPSK}$ are significantly different.
For the quaternary system $(M_X = 4)$ one would have to calculate and analyze the curve $C_{M=4}$ . Again, $C_{M=4} ≤ C_\text{Gauß}$ .
For small $E_{\rm B}/{N_0}$ , $C_{M=4} \approx C_\text{Gauß}$, holds, after which the curve diverges significantly and ends in a horizontal at $C_{M=4} = 2 \ \rm bit/channel use$.

The point $Z$ ⇒ $10 \cdot \lg (E_{\rm B}/{N_0}) = 6 \ \rm dB, \ \ R = 1.5$ lies below $C_{M=4}$.

Such a quaternary system would thus be feasible, as will be shown in Exercise 4.10 .
But only from knowledge of $C_\text{Gauß}$ the question cannot be answered (proposed solution 2).

	For $10 \cdot \lg (E_{\rm B}/{N_0}) = 4 \ \rm dB$ a digital system with rate $R = 1$ and error probability zero can be imagined.
	Such a system does not require channel coding.
	Such a system uses an infinitely long code.
	A binary system can also meet the requirements.

	For $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ a digital system with rate $R = 2$ and error probability zero can be imagined.
	For $10 \cdot \lg (E_{\rm B}/{N_0}) = 0 \ \rm dB$ ⇒ $R = 0.5$ would be sufficient.
	For rate $R = 2$ ⇒ $10 \cdot \lg (E_{\rm B}/{N_0}) = 5 \ \rm dB$ would be sufficient.

	A binary system does not meet the requirements in any case.
	The curve $C_\text{Gaussian}(E_{\rm B}/{N_0})$ is not sufficient for this evaluation.

	A quaternary system does not meet the requirements in any case.
	The curve $C_\text{Gaussian}(E_{\rm B}/{N_0})$ is not sufficient for this evaluation.