Exercise 1.2Z: Sets of Digits

Sets of digits $A$, $B$, $C$

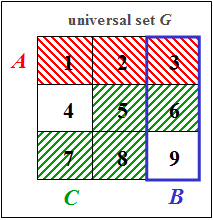
Let the universal set $G$ be the set of all digits between $1$ and $9$. Given are the following subsets:

$$A = \big[\text{digits} \leqslant 3\big],$$

$$ B = \big[\text{digits divisible by 3}\big],$$

$$ C = \big[\text{digits 5, 6, 7, 8}\big],$$

Besides these, let other sets be defined:

$$D = (A \cap \overline B) \cup (\overline A \cap B),$$

$$E = (A \cup B) \cap (\overline A \cup \overline B), $$

$$F = (A \cup C) \cap \overline B, $$

$$G = (\overline A \cap \overline C) \cup (A \cap B \cap C).$$

First consider which digits belong to the sets $D$, $E$, $F$ and $H$ and then answer the following questions.
Justify your answers in terms of set theory.

Hints:

The task belongs to the chapter Set theory basics.

The topic of this chapter is illustrated with examples in the (German language) learning videoMengentheoretische Begriffe und Gesetzmäßigkeiten \Rightarrow.

Questions

Solution

For the other sets defined in the problem holds:

$$ D = (A \cap \overline B) \cup (\overline A \cap B) =\big[\{1, 2, 3\} \cap \{1, 2, 4, 5, 7, 8\}\big] \cup \big[\{4, 5, 6, 7, 8, 9\} \cap \{3, 6, 9\}\big] = \{1, 2, 6, 9\},$$

$$ E = (A \cup B) \cap (\overline A \cup \overline B) = (A \cap \overline A) \cup (A \cap \overline B) \cup (\overline A \cap B) \cup (\overline A \cap \overline B) = (A \cap \overline B) \cup (\overline A \cap B) = D = \{1, 2, 6, 9\},$$

$$F = (A \cup C= \cap \overline B = \{1, 2, 3, 5, 6, 7, 8\} \cap \{1, 2, 4, 5, 7, 8\} = \{1, 2, 5, 7, 8\},$$

$$H = (\bar A \cap \overline C) \cup (A \cap B \cap C) = (\overline A \cap \overline C) \cup \phi = \{4, 9\}.$$

(1) Only the proposed solution 2 is correct:

$A$ and $C$ have no common element.
$A$ and $B$ each contain a $3$.
$B$ and $C$ each contain a $6$.

(2) Correct is the proposed solution 2:

No digit is contained in $A$, $B$ and $C$ at the same time ⇒ $ A \cap B \cap C = \phi$ ⇒ $ \overline{A \cap B \cap C} = \overline{\phi} = G$.
The first proposition, on the other hand, is wrong. It is missing a $4$.

(3) Correct are the proposed solution 1, 2 and 4:

The first proposal is correct: The sets $D$ and $E$ contain exactly the same elements and thus also their complementary sets.
The second proposal is also correct: In general, i.e. for any $X$ and $B$ the following holds: $X \cap \overline B \subset \overline B \ \Rightarrow$ With $X = A \cup C$ it follows that $F \subset \overline B$.
The last proposal is also correct: $A = \{1, 2, 3\},$ $C = \{5, 6, 7, 8\}$ and $H = \{4, 9\}$ form a "complete system".
The third suggestion, on the other hand, is wrong because $B$ and $C$ are not disjoint.

	The complementary sets of $D$ and $E$ are identical.
	$F$ is a subset of the complementary set of $B$.
	The sets $B$, $C$ and $D$ form a complete system.
	The sets $A$, $C$ and $H$ form a complete system.

	$A$ and $B$ are disjoint sets.
	$A$ and $C$ are disjoint sets.
	$B$ and $C$ are disjoint sets.

	The union $A \cup B \cup C$ gives the universal set $G$.
	The complementary set to $A \cap B \cap C$ gives the universal set $G$.