Exercise 1.3: Fictional University Somewhere

Fictional University Somewhere

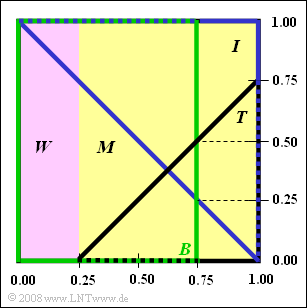
From the adjacent graph you can read some information about $\rm FUS$ (Fictional University Somewhere) ablesen. The whole square represents the universal set $G$ of $960$ students. Of these

$25\%$ female (set $W$, purple rectangle),
$75\%$ male (set $M$, yellow rectangle).

At the university there are the faculties of

Theology (set $T$, black triangle),
Information Technology (set $I$, blue triangle),
Business Administration (set $B$, green triangle).

Each student must be assigned to at least one of these faculties, but can belong to two or three faculties at the same time.

(Bitte diesen Satz überprüfen) The areas in the above diagram are to scale, so you can easily indicate the (percentage) occupancy ("Vielleicht 'enrollment' besser?") figures using the numerical values given and simple geometric considerations.

Hints:

The exercise belongs to the chapter Set Theory Basics.

The topic of this chapter is illustrated with examples in the (German language) learning video Mengentheoretische Begriffe und Gesetzmäßigkeiten $\Rightarrow$ Set Theoretical Concepts and Laws.

Questions

$N_{\rm T} \ = \ $

	$I$ is a subset of $M$.
	$W$ is a subset of $B$.
	$W$ and $M$ together form a complete system.
	$B$, $I$ and $T$ etogether form a complete system.
	$W$ and $T$ are disjoint sets.
	The union of $B$, $I$ and $T$ gives the universal set $G$.
	The intersection of $B$, $I$ and $T$ gives the empty set $\phi$.

$\text{Pr}\big[\text{female IT student}\big] \ = \ $

$\ \%$

$\text{Pr}\big[\text{one field of study}\big] \ = \ $

$\ \%$

$\text{Pr}\big[\text{three fields of study}\big] \ = \ $

$\ \%$

$\text{Pr}\big[\text{two fields of study}\big] \ = \ $

$\ \%$

Solution

(1) From simple geometric considerations, we arrive at the results:

$${\rm Pr}(B) = 3/4 \cdot 1 = 3/4\hspace{0.3cm}(\text{absolute:}\ 720),$$

$${\rm Pr}(I) = {1}/{2}\cdot 1\cdot 1 = 1/2\hspace{0.3cm}(\text{absolute:} \ 480),$$

$${\rm Pr}(T) = {1}/{2} \cdot {3}/{4} \cdot {3}/{4} = {9}/{32} \hspace{0.3cm}(\text{absolute:}\ 270)\hspace{0.3cm}\Rightarrow \hspace{0.3cm}N_{\rm T} \;\underline{= 270}.$$

(2) Proposed solutions 2, 3, 5 and 6 are correct ⇒ proposed solutions 1, 4, 7 are consequently incorrect:

There are also female IT students, although very few.
The union of $B$, $I$ and $T$ gives the universal set, but not a complete system (not all combinations of $B$, $I$ and $T$ are disjoint).
For the same reason, the intersection of $B$, $I$ and $T$ does not yield the empty set.

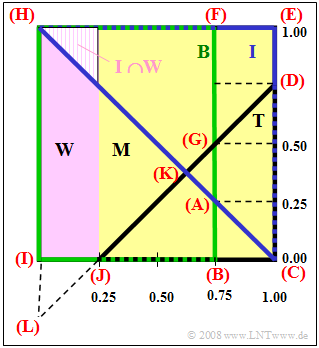
Geometric solution of a probability problem

(3) In set theory, an IT student is the intersection of $I$ and $W$
(shown as a shaded area in the upper left of the graph):

$$\text{Pr[female IT student] = Pr}(I \cap W) = {1}/{2}\cdot {1}/{4} \cdot {1}/{4} = {1}/{32} \hspace{0.15cm}\underline { \thickapprox 3.13 \%}.$$

In words, there are $30$ female IT students among the $960$ students.

(4) The probability can be calculated as the sum of three individual probabilities:

$$ \text{Pr[one field of study] = Pr}( \overline{B} \cap \overline{I} \cap T) + {\rm Pr}( \overline{B} \cap I \cap \overline{T}) + {\rm Pr}( \it B \cap \overline{I} \cap \overline{T}).$$

Each individual probability corresponds to an area in the Venn diagram and can be determined by addition or subtraction of triangles or rectangles (see graph):

$$p_1 = {\rm Pr}( \overline{B} \cap \overline{I} \cap T) = {\rm Triangle\ (ABC)}= \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm}\frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm}\frac{1}{4}= \frac{1}{32}\hspace{0.1cm}\underline{\approx 0.0313},$$

$$p_2 ={\rm Pr}( \overline{B} \cap I \cap \overline{T}) = {\rm Rectangle\hspace{0.1cm}(DEFG)}= \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}+ \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4}\hspace{0.02cm}\cdot \hspace{0.02cm} \frac{1}{4} = \frac{3}{32}\hspace{0.1cm}\underline{\approx 0.0938},$$

$$p_3 = {\rm Pr}( B \cap \overline{I} \cap \overline{T}) ={\rm Rectangle\hspace{0.1cm}(HIJK)}= {\rm Triangle\hspace{0.1cm}(HLK)}- {\rm Triangle\hspace{0.1cm}(ILJ)} = \frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{4}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{5}{8}\hspace{0.02cm} - \hspace{0.02cm}\frac{1}{2}\hspace{0.02cm} \cdot \hspace{0.02cm} \frac{1}{4} \cdot \frac{1}{4} = \frac{23}{64}\hspace{0.1cm}\underline{\approx 0.3594}.$$

$\text{Or:}\hspace{0.3cm}$

$$p_3 = {\rm Triangle\hspace{0.1cm}(HIC)}- {\rm Triangle\hspace{0.1cm}(KJC)} ={1}/{2}\hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} \cdot \hspace{0.1cm} 1 \hspace{0.1cm} - \hspace{0.1cm}{1}/{2}\hspace{0.05cm} \cdot \hspace{0.1cm} {3}/{4} \cdot {3}/{8} = {23}/{64}.$$

The sum of these three probabilities leads to the final result $ \text{Pr[one field of study] } = 31/64 \;\underline {\approx 48.43 \%}$.

(5) This probability is expressed by the triangle $\text{Triangle(AGK)}$ . This has the area

$$\rm Pr[three fields of study] = {1}/{2}\cdot {1}/{4}\cdot {1}/{8} = {1}/{64}\hspace{0.15cm}\underline{\approx 1.56 \%}.$$

(6) The three events

"only one field of study",
"two fields of study" und
"three fields of study"

form a complete system. Thus, using the results of the last subtasks, we obtain:

$$\rm Pr[two fields of study] = 1- \text{Pr[one field of study] } - \rm Pr[three fields of study]= 1- {31}/{64} - {1}/{64} \hspace{0.15cm}\underline{= 50\%}.$$

One would arrive at exactly the same result – but with considerably more effort – in the direct way accordingly:

$${\rm Pr[two fields of study] = Pr}(B\cap I \cap\overline{T}) + {\rm Pr}(B\cap\overline{I}\cap{T}) + {\rm Pr}(\overline{B}\cap I \cap T).$$