Statistical Dependence and Independence

General Definition of Statistical Dependence

So far we have not paid much attention to statistical dependence between events, even though we have already used it as in the case of two disjoint sets: If an element belongs to $A$, it cannot with certainty also be contained in the disjoint set $B$ .

The strongest form of dependence at all is such a deterministic dependence between two sets or two events. Less pronounced is the statistical dependence. Let us start with its complement:

$\text{Definition:}$ Two events $A$ and $B$ are called statistically independent , if the probability of the intersection $A ∩ B$ is equal to the product of the individual probabilities:

$${\rm Pr}(A \cap B) = {\rm Pr}(A)\cdot {\rm Pr}(B).$$

In some applications, statistical independence is obvious, for example, in the "coin toss" experiment. The probability for "heads" or "tails" is independent of whether heads oder tails occurred in the last toss.

And also the individual results in the random experiment "throwing a roulette ball" are always statistically independent of each other under fair conditions, even if individual system players do not want to admit this.

In other applications, on the other hand, the question whether two events are statistically independent or not is not or only very difficult to answer instinctively. Here one can only arrive at the correct answer by checking the formal independence criterion given above, as the following example will show.

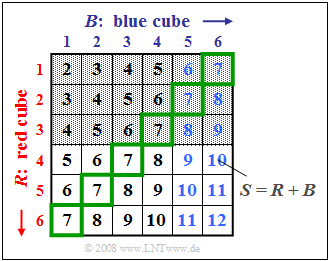
Examples for statistically independent events

$\text{Example 1:}$ We consider the experiment "throwing two dice", where the two dice can be distinguished by their colors red $(R)$ and blue $(B)$ .

The graph illustrates this fact, where the sum $S = R + B$ is entered in the two-dimensional field $(R, B)$ .

For the following description we define the following events:

$A_1$: The number of eyes of the red die is $R < 4$ (red background) ⇒ ${\rm Pr}(A_1) = 1/2$,
$A_2$: The number of eyes of the blue die is $B > 4$ (blue font) ⇒ ${\rm Pr}(A_2) = 1/3$,
$A_3$: The sum of the two dice is $S = 7$ (green outline) ⇒ ${\rm Pr}(A_3) = 1/6$,
$A_4$: The sum of the two dice is $S = 8$ ⇒ ${\rm Pr}(A_4) = 5/36$,
$A_5$: The sum of the two dice is $S = 10$ ⇒ ${\rm Pr}(A_5) = 3/36$.

The graph can be interpreted as follows:

The two events $A_1$ and $A_2$ are statistically independent because the probability ${\rm Pr}(A_1 ∩ A_2) = 1/6$ of the intersection is equal to the product of the two individual probabilities ${\rm Pr}(A_1) = 1/2$ and ${\rm Pr}(A_2) = 1/3$ . Given the problem definition, any other result would also have been very surprising.
But also the events $A_1$ and $A_3$ are statistically independent because of ${\rm Pr}(A_1) = 1/2$, ${\rm Pr}(A_3) = 1/6$ and ${\rm Pr}(A_1 ∩ A_3) = 1/12$ statistisch unabhängig. The probability of intersection $(1/12)$ arises because three of the $36$ squares are both highlighted in red and outlined in green.
In contrast, there are statistical ties between events $A_1$ and $A_4$ because the probability of intersection ⇒ ${\rm Pr}(A_1 ∩ A_4) = 1/18 = 4/72$ is not equal to the product ${\rm Pr}(A_1) \cdot {\rm Pr}(A_4)= 1/2 \cdot 5/36 = 5/72$ .
The two events $A_1$ and $A_5$ are even disjunctive ⇒ ${\rm Pr}(A_1 ∩ A_5) = 0$: none of the boxes with red background is labeled $S=10$ . This example shows that disjunctivity is a particularly pronounced form of statistical dependence.

Conditional Probability

If there are statistical ties between the two events $A$ and $B$ , the (unconditional) probabilities ${\rm Pr}(A)$ and ${\rm Pr}(B)$ do not describe the situation unambiguously in the statistical sense. So-called conditional probabilities are then required.

$\text{Definitions:}$ The conditional probability of $A$ under condition $B$ can be calculated as follows:

$${\rm Pr}(A\hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}(A \cap B)}{ {\rm Pr}(B)}.$$

Similarly, the conditional probability of $B$ under condition $A$ is:

$${\rm Pr}(B\hspace{0.05cm} \vert \hspace{0.05cm}A) = \frac{ {\rm Pr}(A \cap B)}{ {\rm Pr}(A)}.$$

Combining these two equations, we get Bayes' Theorem:

$${\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A) = \frac{ {\rm Pr}(A\hspace{0.05cm} \vert \hspace{0.05cm} B)\cdot {\rm Pr}(B)}{ {\rm Pr}(A)}.$$

Below are some properties of conditional probabilities:

Auch eine bedingte Wahrscheinlichkeit liegt stets zwischen $0$ und $1$ einschließlich dieser beiden Grenzen: $0 \le {\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) \le 1$.
Kann die Bedingung $B$ als konstant angesehen werden, so gelten alle im Kapitel Mengentheoretische Grundlagen für die unbedingten Wahrscheinlichkeiten ${\rm Pr}(A)$ und ${\rm Pr}(B)$ angegebenen Rechenregeln weiterhin.
Sind die existierenden Ereignisse $A$ und $B$ disjunkt, so ist ${\rm Pr}(A\hspace{0.05cm} | \hspace{0.05cm} B) = {\rm Pr}(B\hspace{0.05cm} | \hspace{0.05cm}A)= 0$.
Ist $B$ eine echte oder unechte Teilmenge von $A$, so ist ${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) =1$.
Sind zwei Ereignisse $A$ und $B$ statistisch voneinander unabhängig, so sind deren bedingte Wahrscheinlichkeiten gleich den unbedingten, wie folgende Rechnung zeigt:

$${\rm Pr}(A \hspace{0.05cm} | \hspace{0.05cm} B) = \frac{{\rm Pr}(A \cap B)}{{\rm Pr}(B)} = \frac{{\rm Pr} ( A) \cdot {\rm Pr} ( B)} { {\rm Pr}(B)} = {\rm Pr} ( A).$$

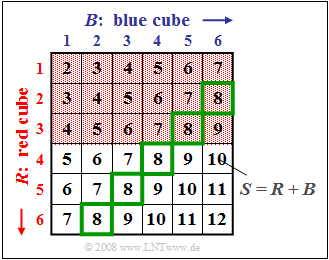
Beispiel für statistisch abhängige Ereignisse

$\text{Beispiel 2:}$ Wir betrachten wieder das Zufallsexperiment "Werfen mit zwei Würfeln", wobei wie im $\text{Beispiel 1}$ $S = R + B$ die Summe des roten und des blauen Würfels bezeichnet.

Wir betrachten hier Bindungen zwischen den beiden Ereignissen

$A_1$: Die Augenzahl des roten Würfels ist $R < 4$ (rote Hinterlegung) ⇒ ${\rm Pr}(A_1) = 1/2$,
$A_4$: Die Summe der beiden Würfel ist $S = 8$ (grüne Umrahmung) ⇒ ${\rm Pr}(A_4) = 5/36$,

und nehmen nochmals Bezug auf das Ereignis

$A_3$: Die Summe der beiden Würfel ist $S = 7$ ⇒ ${\rm Pr}(A_3) = 1/6$.

Zu dieser Grafik ist anzumerken:

Zwischen den Ereignissen $A_1$ und $A_4$ bestehen statistische Bindungen, da die Wahrscheinlichkeit der Schnittmenge ⇒ ${\rm Pr}(A_1 ∩ A_4) = 2/36 = 4/72$ ungleich dem Produkt ${\rm Pr}(A_1) \cdot {\rm Pr}(A_4)= 1/2 \cdot 5/36 = 5/72$ ist.
Die bedingte Wahrscheinlichkeit ${\rm Pr}(A_1 \hspace{0.05cm} \vert \hspace{0.05cm} A_4) = 2/5$ kann aus dem Quotienten der Verbundwahrscheinlichkeit ${\rm Pr}(A_1 ∩ A_4) = 2/36$ und der Wahrscheinlichkeit ${\rm Pr}(A_4) = 5/36$ berechnet werden.
Da $A_1$ und $A_4$ statistisch abhängig sind, ist die bedingte Wahrscheinlichkeit ${\rm Pr}(A_1 \hspace{0.05cm}\vert \hspace{0.05cm} A_4) = 2/5$ (zwei der fünf grün umrandeten Felder sind rot hinterlegt) ungleich der absoluten Wahrscheinlichkeit ${\rm Pr}(A_1) = 1/2$ (die Hälfte aller Felder sind rot hinterlegt).
Ebenso ist die bedingte Wahrscheinlichkeit ${\rm Pr}(A_4 \hspace{0.05cm} \vert \hspace{0.05cm} A_1) = 2/18 = 4/36$ (zwei der $18$ rot hinterlegten Felder sind grün umrandet) ungleich der absoluten Wahrscheinlichkeit ${\rm Pr}(A_4) = 5/36$ (insgesamt sind fünf der $36$ Felder grün umrandet).
Dieses letzte Ergebnis lässt sich zum Beispiel auch über den Satz von Bayes ableiten:

$${\rm Pr}(A_4 \hspace{0.05cm} \vert\hspace{0.05cm} A_1) = \frac{ {\rm Pr}(A_1 \hspace{0.05cm} \vert\hspace{0.05cm} A_4)\cdot {\rm Pr} ( A_4)} { {\rm Pr}(A_1)} = \frac{2/5 \cdot 5/36}{1/2} = 1/9.$$

Dagegen gelten für $A_1$ und das hierzu statistisch unabhängige Ereignis $A_3$ die folgenden bedingten Wahrscheinlichkeiten, siehe Beispiel 1:

$${\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm} A_{\rm 3}) = {\rm Pr}(A_{\rm 1}) = \rm 1/2\hspace{0.5cm}{\rm bzw.}\hspace{0.5cm}{\rm Pr}(A_{\rm 3} \hspace{0.05cm} \vert \hspace{0.05cm} A_{\rm 1}) = {\rm Pr}(A_{\rm 3}) = 1/6.$$

Allgemeines Multiplikationstheorem

Wir betrachten mehrere Ereignisse, die als $A_i$ mit $1 ≤ i ≤ I$ bezeichnet werden. Diese Ereignisse $A_i$ stellen nun aber kein vollständiges System mehr dar, das heißt,

sie sind nicht paarweise zueinander disjunkt, und
es können zwischen den einzelnen Ereignissen auch statistische Bindungen bestehen.

$\text{Definition:}$ Für die so genannte Verbundwahrscheinlichkeit, also für die Wahrscheinlichkeit der Schnittmenge aller $I$ Ereignisse $A_i$, gilt in diesem Fall:

$${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_{I})\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_{I \rm -1} \hspace{0.05cm}\vert \hspace{0.05cm} A_I) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_{I \rm -2} \hspace{0.05cm}\vert\hspace{0.05cm} A_{I - \rm 1}\cap A_I)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...} \hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_{\rm 1} \hspace{0.05cm}\vert \hspace{0.05cm}A_{\rm 2} \cap \hspace{0.02cm}\text{ ...} \hspace{0.1cm}\cap A_{ I}).$$

In gleicher Weise gilt natürlich auch:

$${\rm Pr}(A_{\rm 1} \cap \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cap A_{I}) = {\rm Pr}(A_1)\hspace{0.05cm}\cdot\hspace{0.05cm}{\rm Pr}(A_2 \hspace{0.05cm}\vert \hspace{0.05cm} A_1) \hspace{0.05cm}\cdot \hspace{0.05cm}{\rm Pr}(A_3 \hspace{0.05cm}\vert \hspace{0.05cm} A_1\cap A_2)\hspace{0.05cm} \cdot \hspace{0.02cm}\text{ ...}\hspace{0.1cm} \cdot\hspace{0.05cm} {\rm Pr}(A_I \hspace{0.05cm}\vert \hspace{0.05cm}A_1 \cap \hspace{0.02cm} \text{ ...} \hspace{0.1cm}\cap A_{ I-1}).$$

$\text{Beispiel 3:}$ Eine Lostrommel enthält zehn Lose, darunter drei Treffer $($Ereignis $T_1)$. Dann gilt für die Wahrscheinlichkeit, dass man mit zwei Losen zwei Treffer zieht:

$${\rm Pr}(T_1 \cap T_2) = {\rm Pr}(T_1) \cdot {\rm Pr}(T_2 \hspace{0.05cm }\vert \hspace{0.05cm} T_1) = 3/10 \cdot 2/9 = 1/15 \approx 6.7 \%.$$

Hierbei ist berücksichtigt, dass sich bei der zweiten Ziehung $($Ereignis $T_2)$ nur mehr neun Lose und zwei Treffer in der Urne befänden, falls im ersten Durchgang ein Treffer gezogen worden ist ⇒ ${\rm Pr}(T_2 \hspace{0.05cm} \vert\hspace{0.05cm} T_1) = 2/9$ .
Würde man jedoch die Lose nach der Ziehung wieder in die Trommel zurücklegen, so wären die Ereignisse $T_1$ und $T_2$ statistisch unabhängig und es würde gelten:

$$ {\rm Pr}(T_1 ∩ T_2) = (3/10)^2 = 9\%.$$

Rückschlusswahrscheinlichkeit

Gegeben seien wieder Ereignisse $A_i$ mit $1 ≤ i ≤ I$, die ein vollständiges System bilden. Das heißt:

Alle Ereignisse sind paarweise disjunkt $(A_i ∩ A_j = ϕ$ für alle $i ≠ j$ ).
Die Vereinigungsmenge ergibt die Grundmenge:

$$\rm \bigcup_{\it i=1}^{\it I}\it A_i = \it G.$$

Daneben betrachten wir noch das Ereignis $B$, von dem alle bedingten Wahrscheinlichkeiten ${\rm Pr}(B \hspace{0.05cm} | \hspace{0.05cm} A_i)$ mit den Indizes $1 ≤ i ≤ I$ bekannt sind.

$\text{Satz von der totalen Wahrscheinlichkeit:}$ Unter den oben genannten Voraussetzungen gilt für die (unbedingte) Wahrscheinlichkeit des Ereignisses $B$:

$${\rm Pr}(B) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \cap A_i) = \sum_{i={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert\hspace{0.05cm} A_i)\cdot{\rm Pr}(A_i).$$

$\text{Definition:}$ Aus dieser Gleichung folgt mit dem Satz von Bayes für die Rückschlusswahrscheinlichkeit:

$${\rm Pr}(A_i \hspace{0.05cm} \vert \hspace{0.05cm} B) = \frac{ {\rm Pr}( B \mid A_i)\cdot {\rm Pr}(A_i )}{ {\rm Pr}(B)} = \frac{ {\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_i)\cdot {\rm Pr}(A_i )}{\sum_{k={\rm1} }^{I}{\rm Pr}(B \hspace{0.05cm} \vert \hspace{0.05cm} A_k)\cdot{\rm Pr}(A_k) }.$$

$\text{Beispiel 4:}$ In Münchner Studentenheimen wohnen Studierende

der Ludwig–Maximilian–Universität $($Ereignis $L$ ⇒ ${\rm Pr}(L) = 70\%)$ und
der Technischen Universität München $($Ereignis $T$ ⇒ ${\rm Pr}(T) = 30\%)$.

Es ist weiterhin bekannt, dass an der LMU $60\%$ aller Studierenden weiblich sind, an der TUM nur $10\%$.

Der Anteil aller Studentinnen im Studentenheim $($Ereignis $W)$ kann dann mit dem Satz von der totalen Wahrscheinlichkeit ermittelt werden:

$${\rm Pr}(W) = {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} L)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(L) \hspace{0.05cm}+\hspace{0.05cm} {\rm Pr}(W \hspace{0.05cm} \vert \hspace{0.05cm} T)\hspace{0.01cm}\cdot\hspace{0.01cm}{\rm Pr}(T) = \rm 0.6\hspace{0.01cm}\cdot\hspace{0.01cm}0.7\hspace{0.05cm}+\hspace{0.05cm}0.1\hspace{0.01cm}\cdot \hspace{0.01cm}0.3 = 45 \%.$$

Trifft man eine Studentin, so kann man mit der Rückschlusswahrscheinlichkeit

$${\rm Pr}(L \hspace{-0.05cm}\mid \hspace{-0.05cm}W) = \frac{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L)\cdot {\rm Pr}(L) }{ {\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}L) \cdot {\rm Pr}(L) +{\rm Pr}(W \hspace{-0.05cm}\mid \hspace{-0.05cm}T) \cdot {\rm Pr}(T)}=\rm \frac{0.6\cdot 0.7}{0.6\cdot 0.7 + 0.1\cdot 0.3}=\frac{14}{15}\approx 93.3 \%$$

vorhersagen, dass sie an der LMU studieren wird. Ein durchaus realistisches Ergebnis (zumindest in der Vergangenheit).

Die Aussagen dieses Abschnitts sind im Lernvideo Statistische Abhängigkeit und Unabhängigkeit zusammengefasst.

Aufgaben zum Kapitel

Aufgabe 1.4: 2S/3E-Kanalmodell

Aufgabe 1.4Z: Summe von Ternärgrößen

Aufgabe 1.5: Karten ziehen

Aufgabe 1.5Z: Ausfallwahrscheinlichkeiten