Exercise 2.1: Election Demand

Result of election demand

In an election, the three candidates $A$, $B$ and $C$ are running for mayor.

The candidate who receives more than $50\%$ of the votes cast is elected.
If none of the three candidates succeeds in the first ballot, a runoff election shall be held between the two candidates with the most votes.

Immediately after the closing of the polling stations, the result of an election demand shall be presented:

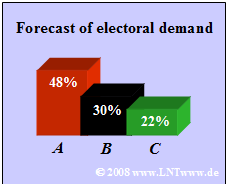
Candidate $A$: $48\%$, Candidate $B$: $30\%$, Candidate $C$: $22\%$.

This demand is based on a survey of only $N = 2000$ of the total $N' = 800 \hspace{0.05cm}000$ voters.

In answering the following questions, assume the following:

The actual (percentage) votes obtained in the election by candidates $A$, $B$ and $C$ can be taken as the probabilities $p_{\rm A}$, $p_{\rm B}$ and $p_{\rm C}$ although these are also themselves determined as relative frequencies $($related to $N')$ .
The $2000$ selected voters ideally represent the entire electorate in a statistical sense and answered truthfully when asked to vote.
According to Bernoulli's Law of Large Numbers the results of this demand are to be understood as relative frequencies:

$$h_{\rm A} = 0.48,\hspace{0.8cm}h_{\rm B} = 0.30,\hspace{0.9cm} h_{\rm C} = 0.22.$$

Hints:

The exercise belongs to the chapter From Random Experiment to Random Variable.

The topic of this chapter is illustrated with examples in the (German language) learning video Bernoullisches Gesetz der großen Zahlen $\Rightarrow$ Bernoulli's Law of Large Numbers.

Questions

Solution

(1) One should at least believe this demand that $\underline{\text{candidate} \ A}$ is likely to win.

(2) The probability that the demand $(h_{\rm A})$ differs from the final outcome $(p_{\rm A})$ by more than $2\%$ is, according to Bernoulli's law of large numbers, with $N = 2000$: $${\rm Pr}(|h_{\rm A} - p_{\rm A}| \geq 0.02) \leq \frac{1}{4 \cdot 2000\cdot 0.02^2} = 0.3125.$$

This probability includes the two equally likely cases that $p_{\rm A} \le 46\%$ and $p_{\rm A} \le 50\%$ is.
Only in the last case there is no runoff:

$${\rm Pr(no\hspace{0.1cm}runoff)} \le 0.156 \hspace{0.15cm}\underline{=15.6 \%}.$$

(3) With $\varepsilon = 4\%$ $($is given by $0.26 -0.22)$ yields the law of large numbers:

$${\rm Pr}\left(|h_{\rm C}-p_{\rm C}|\ge 0.04\right)\le\rm\frac{1}{4\cdot 2000\cdot 0.04^2}=0.078.$$

It follows that:

The probability that candidate $C$ receives at least $26\%$ of the votes is not greater than $3.9\%$.
Since $p_{\rm A} = 0.48$ was assumed fixed, in this case simultaneously $p_{\rm B} \le 0.26$.
Since these are continuous random variables, $(p_{\rm C} \ge 0.26, \; p_{\rm B} \le 0.26)$ and $(p_{\rm C} > 0.26, \; p_{\rm B}< 0.26)$ are equal.
Thus, the probability that $C$ reaches the runoff is also limited to $3.9\%$ :

$${\rm Pr(}C\rm \hspace{0.1cm}reaches\hspace{0.1cm}runoff \hspace{0.1cm}election)\le 0.039 \hspace{0.15cm}\underline{= 3.9 \%}.$$

	candidate $A$,
	Candidate $B$,
	Candidate $C$.