Exercise 2.10Z: Noise with DSB-AM and SSB-AM
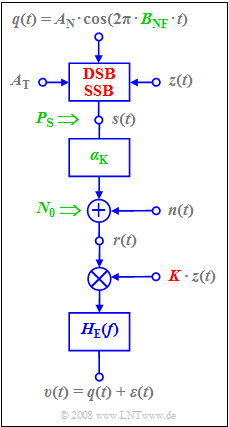
Now the influence of noise on the sink-to-noise ratio $10 · \lg ρ_v$ for both DSB–AM and SSB–AM transmission will be compared. The illustration shows the underlying block diagram.
The differences between the two system variants are highlighted in red on the image, namely the modulator (DSB or SSB) as well as the dimensionless constant
- $$ K = \left\{ \begin{array}{c} 2/\alpha_{\rm K} \\ 4/\alpha_{\rm K} \\ \end{array} \right.\quad \begin{array}{*{10}c} {\rm{bei}} \\ {\rm{bei}} \\ \end{array}\begin{array}{*{20}c} {\rm ZSB} \hspace{0.05cm}, \\ {\rm ESB} \hspace{0.05cm} \\ \end{array}$$
of the receiver-side carrier signal $z_{\rm E}(t) = K · \cos(ω_{\rm T} · t)$, which is assumed to be frequency and phase synchronous with the carrier signal $z(t)$ at the transmitter.
The system parameters captured by the shared performance parameter are labelled in green:
- $$\xi = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}$$
Further note:
- The cosine signal $q(t)$ with frequency $B_{\rm NF}$ stands for a source signal with bandwidth $B_{\rm NF}$ composed of multiple frequencies.
- DSB–AM with carrier is parameterized by a modulation depth of $m = A_{\rm N}/A_{\rm T}$ , while SSB-AM is determined by the sideband-to-carrier ratio $μ = A_{\rm N}/(2 · A_{\rm T})$ .
- The frequency-independent channel transmission factor $α_{\rm K}$ is balanced by the constant $K$ , so that in the noise-free case $(N_0 = 0)$ , the sink signal $v(t)$ matches the source signal $q(t)$ .
- The sink SNR can thus be given as follows $(T_0$ indicates the period of the source signal$)$:
- $$ \rho_{v } = \frac{P_{q}}{P_{\varepsilon }}\hspace{0.5cm}{\rm mit}\hspace{0.5cm} P_{q} = \frac{1}{T_{\rm 0}}\cdot\int_{0}^{ T_{\rm 0}} {q^2(t)}\hspace{0.1cm}{\rm d}t, \hspace{0.5cm}P_{\varepsilon} = \int_{-B_{\rm NF}}^{ +B_{\rm NF}} \hspace{-0.1cm}{\it \Phi_{\varepsilon}}(f)\hspace{0.1cm}{\rm d}f\hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter Single-sideband Modulation.
- Particular reference is made to the page Sideband-to-carrier ratio.
- The results for DSB–AM can be found on the page Sink SNR and the performance parameter.
Questions
Solution
(2) Richtig ist der Lösungsvorschlag 2:
- Bei ZSB–AM ohne Träger gilt $P_{\rm S} = P_q/2$. Dies ist auch gleichzeitig die Leistung des Nutzanteils des Sinkensignals $v(t)$.
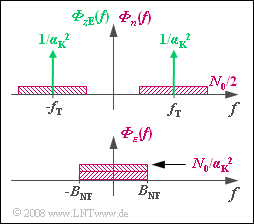
- Das Leistungsdichtespektrum ${\it Φ}_ε(f)$ des Rauschanteils von $v(t)$ ergibt sich aus der Faltung:
- $${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{1}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$
- Der Ausdruck $\big[$ ... $\big]$ beschreibt das Leistungsdichtespektrum eines Cosinussignals mit der Signalamplitude $K = 2$.
- Mit $1/α_K^2$ wird die Korrektur der Kanaldämpfung berücksichtigt.
- Unter Berücksichtigung von ${\it \Phi}_n(f) = N_0/2$ ergibt sich somit:
- $${\it \Phi}_\varepsilon(f) = \frac{N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \int_{-B_{\rm NF}}^{+B_{\rm NF}} {{\it \Phi}_\varepsilon(f) }\hspace{0.1cm}{\rm d}f = \frac{2 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$
- Daraus folgt für das Signal-zu-Rausch-Leistungsverhältnis (SNR):
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}}\hspace{0.15cm}\underline { = \xi} \hspace{0.05cm}.$$
(3) Richtig ist der Lösungsvorschlag 2:
- Bei der ESB gilt im Gegensatz zur ZSB $P_S = P_q/4$ sowie
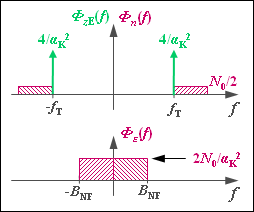
- $${\it \Phi}_\varepsilon(f) = {\it \Phi}_{z{\rm E} }(f) \star {\it \Phi}_n (f) = \frac{4}{\alpha_{\rm K}^2} \cdot \big[\delta(f - f_{\rm T}) + \delta(f + f_{\rm T}) \big]\star {\it \Phi}_n (f) \hspace{0.05cm}.$$
- Unter Berücksichtigung von $B_{\rm HF} = B_{\rm NF}$ (siehe nebenstehende Skizze für die OSB–Modulation) erhält man nun:
- $${\it \Phi}_\varepsilon(f) = \frac{2 \cdot N_0}{\alpha_{\rm K}^2} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} P_\varepsilon = \frac{4 \cdot N_0 \cdot B_{\rm NF}}{\alpha_{\rm K}^2}\hspace{0.05cm}.$$
- Das bedeutet: Verzichtet man auf die Übertragung des Trägers, so zeigt die Einseitenbandmodulation das gleiche Rauschverhalten wie die ZSB–AM.
(4) Ausgehend vom cosinusförmigen Träger mit der Amplitude $A_{\rm T}$ und dem ebenfalls cosinusförmigen Nachrichtensignal $q(t)$ erhält man bei ZSB–AM mit Träger:
- $$ s(t) = \big (q(t) + A_{\rm T}\big ) \cdot \cos( \omega_{\rm T} \cdot t) = A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t) + \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}+ \omega_{\rm N}) \cdot t \big)+ \frac{A_{\rm N}}{2}\cdot \cos\big(( \omega_{\rm T}- \omega_{\rm N}) \cdot t\big)\hspace{0.05cm}.$$
- Die Sendeleistung ergibt sich somit zu
- $$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + 2 \cdot \frac{(A_{\rm N}/2)^2}{2} = \frac{A_{\rm T}^2}{2} + \frac{A_{\rm N}^2}{4} \hspace{0.05cm}.$$
- Unter Berücksichtigung von $P_q = A_{\rm N}^2/2$ und $m = A_{\rm N}/A_{\rm T}$ kann hierfür auch geschrieben werden:
- $$P_{\rm S}= \frac{A_{\rm N}^2}{4} \cdot \left[ 1 + \frac{2 \cdot A_{\rm T}^2}{A_{\rm N}^2}\right] = \frac{P_q}{2} \cdot \left[ 1 + {2 }/{m^2}\right]\hspace{0.05cm}.$$
- Mit der Rauschleistung $P_ε$ gemäß der Teilaufgabe (2) erhält man somit:
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{2 \cdot P_{\rm S}\cdot (1 + 2/m^2)}{2 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{2 }/{m^2}} \hspace{0.05cm}.$$
- Und in logarithmischer Darstellung:
- $$ 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\left[{1 +{2 }/{m^2}}\right] \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 0.5) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (9) \hspace{0.15cm}\underline {= 30.46\, {\rm dB}}$$
- $$\Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \ (m = 1.0) = 40 \,{\rm dB} - 10 \cdot {\rm lg} (3) \hspace{0.15cm}\underline {= 35.23\, {\rm dB} \hspace{0.05cm}}.$$
(5) Bei der ESB–AM gibt es nur ein Seitenband.
- Deshalb gilt unter Berücksichtigung des Seitenband–zu–Träger–Verhältnisses $μ = A_{\rm N}/(2A_{\rm T})$:
- $$ P_{\rm S}= \frac{A_{\rm T}^2}{2} + \frac{(A_{\rm N}/2)^2}{2} = {A_{\rm N}^2}/{8} \cdot \big[ 1 + {4 \cdot A_{\rm T}^2}/{A_{\rm N}^2}\big] = {P_q}/{4} \cdot \big[ 1 + {1 }/{\mu^2}\big] \hspace{0.05cm}.$$
- Somit erhält man mit der Rauschleistung entsprechend der Teilaufgabe (3):
- $$\rho_{v } = \frac{P_{q}}{P_{\varepsilon }} = \frac{4 \cdot P_{\rm S}\cdot (1 + 1/\mu^2)}{4 \cdot N_0 \cdot B_{\rm NF}/\alpha_{\rm K}^2} = \frac{\alpha_{\rm K}^2 \cdot P_{\rm S}}{N_0 \cdot B_{\rm NF}} \cdot \frac{1}{1 +{1 }/{\mu^2}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } = 10 \cdot {\rm lg} \hspace{0.15cm}\xi - 10 \cdot {\rm lg} \hspace{0.15cm}\big[{1 +{1 }/{\mu^2}}\big] \hspace{0.05cm}.$$
- Man erhält also bei der ESB–AM das gleiche Ergebnis wie bei einer ZSB–AM mit dem Modulationsgrad $m = \sqrt{2} · μ$.
- Daraus folgt weiter:
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ESB,} \hspace{0.1cm}\mu = {0.5}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ZSB,} \hspace{0.1cm}m=0.5) \hspace{0.15cm}\underline {=30.46\,{\rm dB}},$$
- $$10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ESB,} \hspace{0.1cm}\mu = {1.0}/{\sqrt{2}}) = 10 \cdot {\rm lg} \hspace{0.15cm}\rho_{v } \hspace{0.15cm}({\rm ZSB,} \hspace{0.1cm}m=1.0) \hspace{0.15cm}\underline {=35.23\,{\rm dB}}\hspace{0.05cm}.$$