Exercise 2.6Z: PN Generator of Length 3
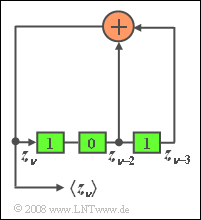
The adjacent sketch shows a PN generator of length $L = 3$ with generator polynomial
- $$G( D) = D^{\rm 3} + D^{\rm 2} + \rm 1$$
and thus the octal identifier $(g_3 \ g_2 \ g_1 \ g_0)$ = $(1 \ 1 \ 0 \ 1)_{\rm bin} = (15)_{\rm oct}$.
The corresponding reciprocal polynomial
- $$G_{\rm R}(D) = D^{\rm 3}\cdot ( D^{\rm -3} + D^{\rm -2} + 1) = D^{\rm 3} + D^{\rm 1} + \rm 1$$
has the octal identifier $(1 \ 0 \ 1 \ 1)_{\rm bin} = (13)_{\rm oct}$.
- At start time, let the three memory cells be preallocated with the binary values $1$, $0$ and $1$ .
- Both arrangements generate an "M-sequence".
Hints:
- The exercise belongs to the chapter Generation of Discrete Random Variables.
- The topic of this chapter is illustrated with examples in the (German language) learning video:
"Erläuterung der PN-Generatoren an einem Beispiel" $\Rightarrow$ "Explanation of PN generators using an example".
Questions
Solution
(1) It is an M-sequence with $L= 3$. It follows that $P= 2^L - 1 \hspace{0.15cm}\underline{= 7}$.
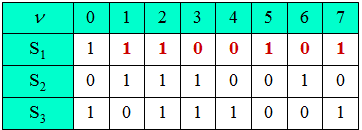
(2) We denote the cells from left to right by $S_1$, $S_2$ and $S_3$. Then holds:
- $S_2(\nu) = S_1(\nu - 1)$,
- $S_3(\nu) = S_2(\nu - 1)$,
- $S_1(\nu) = S_2(\nu - 1) \ {\rm mod } \ S_3(\nu - 1)$.
The result is entered in the first row of the above table (marked in red):
- At the clock time $\nu = 7$ results in the same memory usage as at the time $\nu = 0$.
- From this follows $ {P = 7}$ and the sequence is from $\nu = 1$ corresponding to solution 3 :
- $$\langle z_\nu \rangle = 1 \ 1 \ 0 \ 0 \ 1 \ 1 \ 0 \ 0 \ 1 \ 0 \ 1 \ 1 \text{...}$$
- In contrast, proposal 1 describes the M sequence of the PN generator with length $L=4$ and identifier $(31)$ ⇒ period length is $P= 15$.
- In proposal 2, the period length $P= 4$ is too short.
- Finally, the last proposal would have the desired period length $P= 7$, but from the modulo 2 addition of $S_2= 0$ and $S_3= 1$ $($für $\nu = 0)$ it necessarily follows at the next time $(\nu = 1)$ : $S_1= 1$. This property is not exhibited by sequence 4.
(3) Correct are solutions 2, 3, and 4:
- The maximum number of consecutive ones is $L$ (namely if there is a one in all $L$ memory cells).
- On the other hand, it is not possible that all memory cells are filled with zeros. Therefore, there is always one more than zeros.
- The period length of the last sequence is $P = 2$. On the other hand, for an M-sequence $P= 2^L - 1.$ For no value of $L$ is $P = 2$ possible.
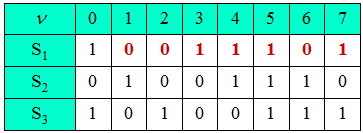
(4) In the adjacent table the emergence of the PN–sequence at the reciprocal polynomial $G_{\rm R}(D)$ is entered. It can be seen that the proposed solution 2 applies:
- Also for the reciprocal arrangement, the period length $P = 7$ must hold, so that proposition 1 $($with $P = 15)$ is eliminated.
- Proposal 3 is just a version of the initial sequence of $(15)$ shifted by two clocks.
- In contrast, in the (correct) second proposal, the inverse of ... $ 1 \ 1 \ 0 \ 1 \ 0 \ 1$ ... – thus the sequence ... $ 1 \ 0 \ 1 \ 0 \ 0 \ 1 \ 1$ ... – are included, albeit with a phase shift.