Exercise 3.12: Cauchy Distribution

• Return to book

PDF of Cauchy distribution

The probability density function of the Cauchy distribution is given as follows:

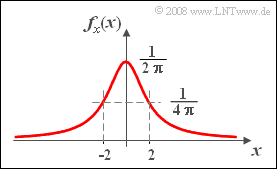
$$f_x(x)=\frac{\rm 1}{\rm 2 \pi}\cdot \frac{\rm 1}{\rm 1+ (\it x/\rm 2)^{\rm 2}}.$$

From the graph you can already see the extremely slow decay of the PDF course.

Hints:

• The exercise belongs to the chapter  Further Distributions.
• In particular, reference is made to the page  Cauchy PDF .

Questions

1

What is the distribution function  $F_x(r)$?  What is the probability that  $x$  is smaller than  $2$ by a small amount?

${\rm Pr} (|x| < 2) \ = \ $ $\ \%$

2

What is the probability that  $x$  is greater in amount than  $4$?

${\rm Pr} (|x| > 4) \ = \ $ $\ \%$

3

Which of the following statements are true for the Cauchy distribution?

	The Cauchy distribution has an infinitely large variance.
	The Chebyshev inequality makes no sense here.
	A random variable that can be measured in nature is never Cauchy distributed.

Solution

Solution

(1)  Comparing the given PDF with the general equation in the theory part, we see that the parameter  $\lambda= 2$  is.

• From this follows  (after integration over the PDF):

$$F_x ( r ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(\it r/\rm 2).$$

• In particular.

$$F_x ( r = +2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(1)=\frac{1}{2} + \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.75,$$

$$F_x ( r = -2 ) =\frac{1}{2} + \frac{\rm 1}{\rm \pi}\cdot \rm arctan(-1)=\frac{1}{2} - \frac{\rm 1}{\rm \pi} \cdot \frac{\rm \pi}{4 }=0.25.$$

• The probability we are looking for is given by the difference of.

$${\rm Pr} (|x| < 2) = 0.75 - 0.25 \hspace{0.15cm}\underline{=50\%}.$$

(2)  According to the result of the subtask  (1)  is  $F_x ( r = 4 ) = 0.5 + 1/\pi = 0.852$.

• Thus, for the "complementary" probability  ${\rm Pr} (x > 4)= 0.148$.
• For symmetry reasons, the probability we are looking for is twice as large:

$${\rm Pr} (|x| >4) \hspace{0.15cm}\underline{ = 29.6\%}.$$

(3)  All proposed solutions are true:

• For the variance of the Cauchy distribution holds namely:

$$\sigma_x^{\rm 2}=\frac{1}{2\pi}\int_{-\infty}^{+\infty} \hspace{-0.15cm} \frac{\it x^{\rm 2}}{\rm 1+(\it x/\rm 2)^{\rm 2}} \,\,{\rm d}x.$$

• For große  $x$  the integrand yields the constant value  $4$. Therefore the integral diverges.
• With  $\sigma_x \to \infty$  however, even Chebyshev's inequality does not provide an evaluable bound.
• Natural" random variables (physically interpretable) can never be cauchy distributed, otherwise they would have to have infinite power.
• On the other hand, an "artificial" (or mathematical) random variable (example: the quotient of two zero mean quantities) is not subject to this restriction.