Exercise 5.2Z: Two-Way Channel

Two–way channel impulse response $h(t)$ and $h(t) * h( { - t} )$

It is known from a transmission system that the following relationship exists between the input signal $x(t)$ and the output signal $y(t)$ :

$$y(t) = x( {t - \tau _1 } ) + \alpha \cdot x( {t - \tau _2 } ).$$

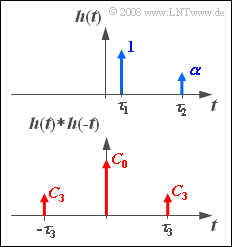
The corresponding impulse response $h(t)$ is sketched above.

In the sketch below, the function

$$h(t) * h( { - t} )\hspace{0.25cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.25cm}\left| {H(f)} \right|^2$$

is shown, where the parameters $C_0$, $C_3$ and $\tau_3$ depend on $\alpha$, $\tau_1$ and $\tau_2$ ⇒ see subtask (4).

Let the input signal $x(t)$ be band-limited white noise

with power density $N_0 = 10^{-6} \hspace{0.08cm} \rm W/Hz$
and the bandwidth $B = 10 \hspace{0.08cm} \rm kHz$,

from which the power $P_x = 10 \hspace{0.08cm} \rm mW$ can be calculated.

Notes:

The exercise belongs to the chapter Stochastic System Theory.
Always use the value $\alpha = 0.5$ for the numerical calculations.
For the subtasks (1) and (2) let $\tau_1 = 0$ and $\tau_2 = 4\hspace{0.08cm}\rm ms$ be valid.
For later tasks, assume $\tau_1 = 1\hspace{0.08cm}\rm ms$ and $\tau_2 = 5\hspace{0.08cm}\rm ms$.

Questions

$f_0 \ = \ $

$\ \rm kHz$

$|H(f = 0)|^2 \ = \ $

$C_0 \ = \ $

$C_3 \ = \ $

$\tau_3 \ = \ $

$\ \rm ms$

$P_y \ = \ $

$\ \rm mW$

Solution

(1) $H(f)$ is the Fourier transform to $h(t)$.

Using the shifting theorem, this is $(\tau_1 = 0)$:

$$H(f) = 1 + \alpha \cdot {\rm{e}}^{ - {\rm{j2\pi }}f\tau _2 } = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$

If $H(f)$ is periodic with $f_0$, then for all integer values of $i$ must hold:

$$H( {f + i \cdot f_0 } ) = H( f ).$$

With $f_0 = 1/\tau_2\hspace{0.15cm} \underline{= 0.25 \hspace{0.05cm}\rm kHz}$ this condition is satisfied.

$$H( {f + i \cdot f_0 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 + i{\rm{2\pi }}f_0 \tau _2 } ) = 1 + \alpha \cdot \cos ( {{\rm{2\pi }}f\tau _2 } ) - {\rm{j}} \cdot \alpha \cdot \sin ( {{\rm{2\pi }}f\tau _2 } ).$$

(2) The magnitude square is the sum of squared real part and squared imaginary part:

$$\left| {H( f )} \right|^2 = \left( {1 + \alpha \cdot \cos ( A )} \right)^2 + \left( {\alpha \cdot \sin ( A )} \right)^2 .$$

Here the angle argument is abbreviated as $A = 2\pi f \tau$. After multiplying out, we get because of $\cos^2(A) + \sin^2(A) = 1$:

$$\left| {H(f)} \right|^2 = 1 + \alpha ^2 + 2\alpha \cdot \cos ( A ).$$

At the frequency $f = 0$ $($and thus $A = 0)$, the general result or with $\alpha = 0.5$ is:

$$\left| {H( {f = 0} )} \right|^2 = \left( {1 + \alpha } \right)^2 = 1.5^2\hspace{0.15cm} \underline{ = 2.25}.$$

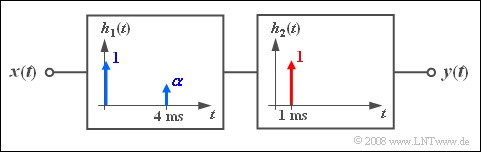
(3) Now the transmission system can be composed of two subsystems (see diagram):

Division of the impulse response into two subsystems

The transfer function $H_1(f)$ is calculated as in subtask (2).
For $H_2(f)$ it holds with $\tau_1 = 1\hspace{0.05cm}\rm ms$:

$$H_2 (f) = {\rm{e}}^{ - {\rm{j2\pi }}f\tau _1 } \quad \Rightarrow \quad \left| {H_2 (f)} \right| = 1\quad \Rightarrow \quad \left| {H_2 (f)} \right|^2 = 1.$$

This means: Due to the additional running time, $\left| {H(f)} \right|^2$ is not changed compared to subtask (2).
At the frequency $f = 0$, $\left| {H(f = 0)} \right|^2\hspace{0.15cm} \underline{ = 2.25}$ is still valid.

(4) By comparing the drawn function $h(t) \star h(-t)$ with the result of subtask (2) we obtain:

$$C_0 = 1 + \alpha ^2 \hspace{0.15cm} \underline{= 1.25}, \hspace{0.5cm}C_3 = \alpha \hspace{0.15cm} \underline{= 0.5}, \hspace{0.5cm}\tau _3 = \tau _2 - \tau _1 \hspace{0.15cm} \underline{= 4\;{\rm{ms}}}.$$

(5) The PDS of the output signal $y(t)$ is limited to the range of $\pm B$ and results in

$${\it \Phi}_y(f) = {N_0}/{2} \cdot |H(f)|^2 = N_0/{2} \cdot {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}.$$

Taking advantage of symmetry properties, we thus obtain for the power:

$$P_y = N_0 \cdot \int_0^B {\left( {1 + \alpha ^2 + 2\alpha \cdot \cos ( {2{\rm{\pi }}f\tau _3 } )} \right)}\hspace{0.1cm} {\rm{d}}f.$$

$B = 10 \hspace{0.08cm} \rm kHz$ is an integer multiple of the frequency period $f_0 = 1/\tau_2= 250 \hspace{0.08cm}\rm Hz$ $($cf. solution to subtask 1$)$.
Therefore, the cosine function does not contribute to the integral, and we obtain:

$$P_y = N_0 \cdot B \cdot \left( {1 + \alpha ^2 } \right) = 1.25 \cdot P_x \hspace{0.15cm} \underline{ = 12.5\;{\rm{mW}}}.$$