Exercise 4.09: Cyclo-Ergodicity
From LNTwww
Revision as of 09:39, 28 January 2022 by Guenter (talk | contribs) (Guenter moved page Aufgabe 4.09: Zykloergodizität to Exercise 4.09: Cyclo-Ergodicity)
Wir betrachten zwei unterschiedliche Zufallsprozesse, deren Musterfunktionen harmonische Schwingungen mit jeweils gleicher Frequenz $f_0 = 1/T_0$ sind. $T_0$ bezeichnet die Periodendauer.
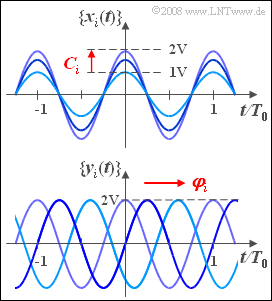
- Beim oben dargestellten Zufallsprozess $\{x_i(t)\}$ ist die stochastische Komponente die Amplitude, wobei der Zufallsparameter $C_i$ alle Werte zwischen $1\hspace{0.05cm}\rm V$ und $2\hspace{0.05cm}\rm V$ mit gleicher Wahrscheinlichkeit annehmen kann:
- $$\{ x_i(t) \} = \{ C_i \cdot \cos (2 \pi f_{\rm 0} t)\}. $$
- Beim Prozess $\{y_i(t)\}$ weisen alle Musterfunktionen die gleiche Amplitude auf: $x_0 = 2\hspace{0.05cm}\rm V$. Hier variiert die Phase $\varphi_i$, die über alle Musterfunktionen gemittelt gleichverteilt zwischen $0$ und $2\pi$ ist:
- $$\{ y_i(t) \} = \{ x_{\rm 0} \cdot \cos (2 \pi f_{\rm 0} t - \varphi_i)\}. $$
Die Eigenschaften "zyklostationär" und "zykloergodisch" sagen aus,
- dass die Prozesse zwar im strengen Sinne nicht als stationär und ergodisch zu bezeichnen sind,
- alle statistischen Kennwerte aber für Vielfache der Periondauer $T_0$ jeweils gleich sind.
In diesen Fällen sind auch die meisten der Berechnungsregeln anwendbar, die eigentlich nur für ergodische Prozesse gelten.
Hinweis:
- Die Aufgabe gehört zum Kapitel Autokorrelationsfunktion.
Fragebogen
Musterlösung
(1) Richtig sind die Lösungsvorschläge 3 und 4:
- Zum Zeitpunkt $t = 0$ $($und allen Vielfachen der Periodendauer $T_0)$ hat jedes Mustersignal $x_i(t)$ einen Wert zwischen $1\hspace{0.05cm}\rm V$ und $2\hspace{0.05cm}\rm V$. Der Mittelwert ist $1.5\hspace{0.05cm}\rm V$.
- Dagegen ist bei $t = T_0/4$ der Signalwert des gesamten Ensembles identisch Null. Das heißt:
- Bereits der lineare Mittelwert erfüllt die Bedingung der Stationarität nicht: Der Prozess $\{x_i(t)\}$ ist nicht stationär und kann deshalb auch nicht ergodisch sein.
- Dagegen sind beim Prozess $\{y_i(t)\}$ aufgrund der gleichverteilten Phase zu allen Zeitpunkten die gleichen Momente zu erwarten ⇒ der Prozess ist stationär.
- Da bei der AKF-Berechnung die Phasenbeziehungen verloren gehen, steht jede einzelne Musterfunktion stellvertretend für den gesamten Prozess. Deshalb kann hier hypothetisch von Ergodizität ausgegangen werden.
- Am Ende der Aufgabe ist zu überprüfen, ob diese Annahme gerechtfertigt ist.
(2) Aufgrund der Ergodizität kann jede Musterfunktion zur AKF–Berechung herangezogen werden. Wir benutzen hier willkürlich die Phase $\varphi_i = 0$.
- Aufgrund der Periodizität genügt die Mitteilung über nur eine Periodendauer $T_0$. Dann gilt:
- $$\varphi_y (\tau) = \frac{1}{T_0} \cdot \int_0^{T_0} y(t) \cdot y (t+\tau) \hspace{0.1cm}{\rm d} t = \frac{{ x}_0^2}{{ T}_0} \cdot \int_0^{{\it T}_0} \cos (2 \pi {f_{\rm 0} t}) \cdot \cos (2 \pi {f_{\rm 0} (t+\tau)}) \hspace{0.1cm}\rm d \it t.$$
- Mit der trigonometrischen Beziehung $\cos (\alpha) \cdot \cos (\beta)= {1}/{2} \cdot \cos (\alpha + \beta) + {1}/{2} \cdot \cos (\alpha - \beta)$ folgt daraus weiter:
- $$\varphi_y (\tau) = \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (4 \pi \it{f_{\rm 0} t} + {\rm 2} \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t \ {\rm +} \ \rm \frac{{\it x}_0^2}{{2 \it T}_0} \cdot \int_0^{{\it T}_0} \rm cos (-2 \pi \it{f_{\rm 0} \tau}{\rm )} \hspace{0.1cm}\rm d \it t. $$
- Das erste Integral ist Null (Integration über zwei Perioden der Cosinusfunktion).
- Der zweite Integrand ist unabhängig von der Integrationsvariablen $t$. Daraus folgt: $\varphi_y (\tau) ={{ x}_0^2}/{\rm 2} \cdot \cos (2 \pi {f_{\rm 0} \tau}). $
- Für die angegebenen Zeitpunkte gilt mit $x_0 = 2\hspace{0.05cm}\rm V$:
- $$\varphi_y (0)\hspace{0.15cm}\underline{ = 2\hspace{0.05cm}{\rm V}^2}, \hspace{0.5cm} \varphi_y (0.25 \cdot { T}_{\rm 0}{\rm )} \hspace{0.15cm}\underline{ = 0}, \hspace{0.5cm} \varphi_y (\rm 1.5 \cdot {\it T}_{\rm 0} {\rm )} \hspace{0.15cm}\underline{= \rm -2\hspace{0.05cm}{\rm V}^2}.$$
(3) Richtig sind beiden ersten Lösungsvorschläge:
- Der Mittelwert $m_y$ kann aus dem Grenzwert der AKF für $\tau \to \infty$ ermittelt werden, wenn man die periodischen Anteile ausschließt. Daraus folgt $m_y= 0$.
- Die Varianz (Leistung) ist gleich dem AKF–Wert an der Stelle $\tau = 0$, also $2\hspace{0.05cm}\rm V^2$. Der Effektivwert ist die Quadratwurzel daraus: $\sigma_y \approx 1.414\hspace{0.05cm}\rm V$.
- Die Periodendauer eines periodischen Zufallsprozesses bleibt in der AKF erhalten, das heißt, auch die Periodendauer der AKF beträgt $T_0$.