Exercise 5.2: Determination of the Frequency Response

Determining the frequency response $H(f)$

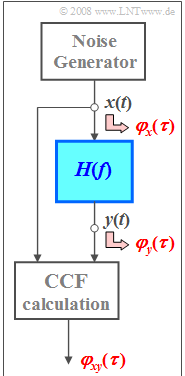
We consider the illustrated measurement setup for the determination of the frequency response $H(f)$ highlighted in blue.

The input signal $x(t)$ is white Gaussian noise with the noise power density $N_0 = 10^{-10} \hspace{0.05cm} \rm W/Hz$.
Thus, the auto-correlation function (ACF) is:

$$\varphi _x ( \tau ) = {N_0 }/{2} \cdot \delta ( \tau ).$$

The measured cross-correlation function (CCF) between the signals $x(t)$ and $y(t)$ can be approximated as follows
$($valid only for positive times $t)$:

$$\varphi _{xy} \left( \tau \right) = K \cdot {\rm{e}}^{ - \tau /T_0 },\hspace{0.5cm}\text{mit } \ K = 0.628 \cdot 10^{-12} \hspace{0.05cm} {\rm W}, \ T_0 = 1 \hspace{0.05cm} \rm ms.$$

The ACF $\varphi_y(\tau)$ of the output signal $y(t)$ is also measured.

Notes:

The exercise belongs to the chapter Stochastic System Theory.
Reference is also made to the chapter Power Density Spectrum.

Please also note the following Fourier transform $($in $\omega)$:

$$H( \omega ) = \frac{1}{{1 + {\rm{j}}\cdot \omega /\omega _0 }}\hspace{0.15cm}\bullet\!\!\!-\!\!\!-\!\!\!-\!\!\circ\,\hspace{0.15cm}h(t) = \omega _0 \cdot {\rm{e}}^{ - \omega _0 t} \hspace{0.3cm}(t \ge 0).$$

For negative $t$ values, on the other hand, $h(t) =0$ at all times.

Questions

	the functions $\varphi_x(\tau)$ and $\varphi_y(\tau)$ are known,
	the functions $\varphi_x(\tau)$ and $\varphi_{xy}(\tau)$ are known,
	the functions $\varphi_{xy}(\tau)$ and $\varphi_y(\tau)$ are known.

$h(t = T_0) \ = \ $

$\ \cdot 10^{-3} \ \rm 1/s$

$H(f = 0) \ = \ $

${\it \Phi}_y(f = 1/(2\pi T_0)) \ = \ $

$\ \cdot 10^{-12}\ \rm W/Hz$

Solution

(1) Statements 2 and 3 are true.

The following equations are valid:

$$\varphi _{xy} ( \tau ) = h( \tau ) * \varphi _x ( \tau )\quad \Rightarrow \quad H( f ) = \frac{{{\it \Phi} _{xy} ( f )}}{{{\it \Phi} _x ( f )}},$$

$$\varphi _y ( \tau) = \varphi _{xy} ( \tau) * h(- \tau)\quad \Rightarrow \quad H^{\star}( f ) = \frac{{{\it \Phi} _y ( f )}}{{{\it \Phi} _{xy} ( f )}}.$$

In contrast, the first statement is false: the phase relations are lost in the ACF calculation.
The associated spectral functions to $\varphi_x(\tau)$ and $\varphi_x(\tau)$ – namely ${\it \Phi}_x(f)$ and ${\it \Phi}_y(f)$ – are purely real, so only the magnitude $|H(f)|$ can be given.

(2) For dirac-shaped input ACF $\varphi_x(\tau)$, the impulse response $h(t)$ is equal in shape to the CCF:

$$h(t) = \frac{{K \cdot {\rm{e}}^{ - t/T_0 } }}{N_0 /2} = 1.256 \cdot 10^{ - 2} \frac{1}{{\rm{s}}} \cdot {\rm{e}}^{ - t/T_0 } \hspace{0.3cm}\Rightarrow \hspace{0.3cm}h(t = T_0)\hspace{0.15cm}\underline{ = 4.62 \cdot 10^{-3}\ \rm 1/s}.$$

(3) The Fourier correspondence given is with $T_0 = 1/\omega_0$ and the constant $C= N_0/2 \cdot T_0/K$:

$$h(t) = \frac{C}{T_0 } \cdot {\rm{e}}^{ - t/T_0 }\hspace{0.15cm}\circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\hspace{0.15cm} H( \omega ) = \frac{C}{{1 + {\rm{j}}\cdot \omega T_0 }}.$$

The constant results in $C = 0.08$. With $H(f) = 2 \pi \cdot H(\omega)$ it follows:

$$H(f) = \frac{0.5}{1 + {\rm{j\cdot 2\pi }}\cdot fT_0 } \hspace{0.3cm}\Rightarrow \hspace{0.3cm} H(f= 0) \hspace{0.15cm}\underline{=0.5}.$$

(4) For the output PDS, in general, or specifically here:

$${\it \Phi}_y (f) = {\it \Phi} _x (f) \cdot \left| {H(f)} \right|^2 = \frac{N_0 }{2} \cdot \frac{0.5^2 }{{\left( {1 + {\rm{j\cdot 2\pi }}\cdot fT_0 } \right)\left( {1 - {\rm{j\cdot 2\pi }}\cdot fT_0 } \right)}} = {N_0 }/{8} \cdot \frac{1}{1 + \left( {{\rm{2\pi }}\cdot fT_0 } \right)^2 }.$$

At the given frequency $f = 1/(2\pi T_0)$, ${\it \Phi}_y (f)$ has dropped by half compared to its maximum at $f=0$ :

$${\it \Phi}_y (f = 1/(2 \pi T_0)) ={N_0 }/{16}\hspace{0.15cm} \underline{ = 6.25 \cdot 10^{ - 12} \;{\rm{W/Hz}}}.$$