Contents
- 1 General description
- 2 Probability density function – Cumulative density function
- 3 Exceedance probability
- 4 Central moments and moments
- 5 Gaussian generation by addition method
- 6 Gaussian generation with the Box/Muller method
- 7 Gaussian generation with the "Tabulated Inversion" method
- 8 Exercises for the chapter
- 9 References
General description
Random variables with Gaussian probability density function - the name goes back to the important mathematician, physicist and astronomer Carl Friedrich Gauss - are realistic models for many physical variables and are also of great importance for communications engineering.
$\text{Definition:}$ To describe the Gaussian distribution, we consider a sum of $I$ statistical variables:
- $$x=\sum\limits_{i=\rm 1}^{\it I}x_i .$$
- According to the central limit theorem of statistics this sum has a Gaussian PDF in the limiting case $(I → ∞)$ as long as the individual components $x_i$ have no statistical ties. This holds (almost) for all density functions of the individual summands.
- Many "noise processes" fulfill exactly this condition, that is, they are additively composed of a large number of independent individual contributions, so that their pattern functions ("noise signals") exhibit a Gaussian amplitude distribution.
- If one applies a Gaussian distributed signal to a linear filter for spectral shaping, the output signal is also Gaussian distributed. Only the distribution parameters such as mean and standard deviation change, as well as the internal statistical ties of the samples
.
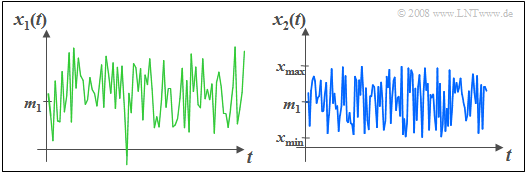
$\text{Example 1:}$ The graph shows in comparison.
- on the left, a Gaussian random signal $x_1(t)$ and
- on the right, an uniformly distributed signal $x_2(t)$
with equal mean $m_1$ and equal standard deviation $σ$.
It can be seen that with the Gaussian distribution, in contrast to the uniform distribution.
- any large and any small amplitude values can occur,
- even if they are improbable compared to the mean amplitude range
.
Probability density function – Cumulative density function
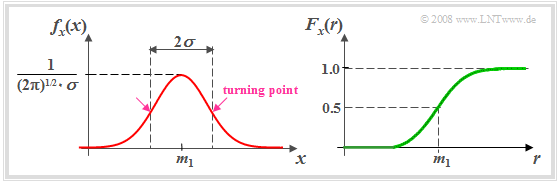
$\text{Definition:}$ The probability density function $\rm (PDF)$ of a Gaussian distributed random variable $x$ is generally:
$$\hspace{0.4cm}f_x(x) = \frac{1}{\sqrt{2\pi}\cdot\sigma}\cdot {\rm e}^{-(x-m_1)^2 /(2\sigma^2) }.$$ The parameters of such a Gaussian PDF are.
- $m_1$ ("mean" or "DC component"),
- $σ$ ("standard deviation").
If $m_1 = 0$ and $σ = 1$, it is often referred to as the "normal distribution".
From the left plot, it can be seen that the standard deviation $σ$ can also be determined graphically as the distance from the maximum value and the inflection point from the bell-shaped PDF $f_{x}(x)$.
On the right the cumulative distribution function $F_{x}(r)$ of the Gaussian distributed random variable is shown. It can be seen:
- The CDF is point symmetric about the mean $m_1$.
- By integration over the Gaussian PDF one obtains:
- $$F_x(r)= \phi(\frac{\it r-m_{\rm 1}}{\sigma})\hspace{0.5cm}\rm with\hspace{0.5cm}\rm \phi (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\it \pi}}\int_{-\rm\infty}^{\it x} \rm e^{\it -u^{\rm 2}/\rm 2}\,\, d \it u.$$
- One calls $ϕ(x)$ the Gaussian error integral. This function cannot be calculated analytically and must therefore be taken from tables.
- $ϕ(x)$ can be approximated by a Taylor series or calculated from the function ${\rm erfc}(x)$ often available in program libraries.
The topic of this chapter is illustrated with examples in the (German language) learning video "Der AWGN-Kanal" $\Rightarrow$ "The AWGN channel", especially in the second part.
Exceedance probability
In the study of digital transmission systems, it is often necessary to determine the probability that a (zero mean) Gaussian distributed random variable $x$ with variance $σ^2$ exceeds a given value $x_0$.
$\text{Definition:}$ For this exceedance probability holds:
- $${\rm Pr}(x > x_{\rm 0})={\rm Q}({x_{\rm 0} }/{\sigma}).$$
- Here, ${\rm Q}(x) = 1 - {\rm ϕ}(x)$ denotes the complementary function to $ {\rm ϕ}(x)$. This function is called the Complementary Gaussian error integral and the following calculation rule applies:
- $$\rm Q (\it x\rm ) = \rm 1- \phi (\it x)$$
- $$\Rightarrow \hspace{0.3cm}\rm Q (\it x\rm ) = \frac{\rm 1}{\sqrt{\rm 2\pi} }\int_{\it x}^{\rm +\infty}\hspace{-0.4cm}\rm e^{\it - u^{\rm 2}/\hspace{0.05cm} \rm 2}\,d \it u .$$
- ${\rm Q}(x)$ like ${\rm \phi}(x)$ is not analytically solvable and must be taken from tables.
- In libraries one often finds the function ${\rm erfc}(x)$ related to ${\rm Q}(x)$ as follows:
- $${\rm Q}(x)={\rm 1}/\hspace{0.05cm}{\rm 2}\cdot \rm erfc({\it x}/{\sqrt{\rm 2} }).$$
Especially for larger $x$-values (i.e., for small error probabilities) the bounds given below provide useful estimates for the complementary Gaussian error integral:
- Upper bound (German: "obere Schranke" ⇒ subscript: "o"):
- $${\rm Q_o}(x ) \ge {\rm Q}(x)=\frac{ 1}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{- x^{2}/\hspace{0.05cm}2}. $$
- Lower bound (German: "untere Schranke" ⇒ subscript: "u"):
- $${\rm Q_u}(x )\le {\rm Q}(x)=\frac{\rm 1-{\rm 1}/{\it x^{\rm 2}}}{\sqrt{\rm 2\pi}\cdot \it x}\cdot \rm e^{-\it x^{\rm 2}/\hspace{0.05cm}\rm 2} =\rm Q_0(\it x \rm ) \cdot \left(\rm 1-{\rm 1}/{\it x^{\rm 2}}\right) .$$
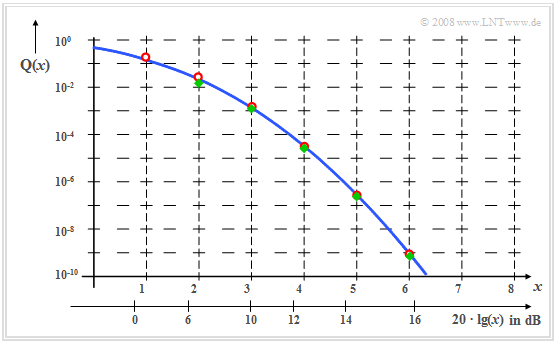
$\text{Conclusion:}$ The upper graph shows the function $\rm Q$ in logarithmic representation for linear (upper $x$–axis) and logarithmic abscissa values (lower axis).
- The upper bound ${\rm Q_o}(x )$ (red circles) is useful from about $x = 1$ and the lower bound ${\rm Q_u}(x )$ (green diamonds) from $x ≈ 2$.
- For $x ≥ 4$ both bounds are indistinguishable from the actual course ${\rm Q}(x)$ within character precision.
The interactive HTML5/JavaScript applet "Complementary Gaussian Error Functions" provides
- the numerical values of the functions ${\rm Q}(x)$ and $1/2 \cdot {\rm erfc}(x)$
- including the two bounds given here.
Central moments and moments
The characteristics of the Gaussian distribution have the following properties:
- The central moments $\mu_k$ $($identical to the moments $m_k$ of the equivalent zero mean random variable $x - m_1$ are identically zero for the Gaussian PDF as well as for the uniform distribution due to the symmetric relations for odd values of $k$ .
- The second central moment is by definition equal to $\mu_2 = σ^2$.
- All higher central moments with even values of $k$ can be expressed by the variance $σ^2$ for the Gaussian PDF - mind you: exclusively for this one:
- $$\mu_{k}=(k- 1)\cdot (k- 3) \ \cdots \ 3\cdot 1\cdot\sigma^k\hspace{0.2cm}\rm (if\hspace{0.1cm}\it k\hspace{0.1cm}\rm even).$$
- From this, the noncentered moments $m_k$ can be determined as follows:
- $$m_k = \sum\limits_{\kappa= 0}^{k} \left( \begin{array}{*{2}{c}} k \\ \kappa \\ \end{array} \right)\cdot \mu_\kappa \cdot {m_1}^{k-\kappa}.$$
- This last equation holds in general, i.e., for arbitrary distributions.
$\text{Conclusion:}$
- From the above equation it follows directly $\mu_4 = 3 \cdot σ^4$ and from it for the kurtosis the value $K = 3$.
- For this reason, one often refers to $K-3$ as the "Gaussian deviation" or as the "excess".
- If the Gaussian deviation is negative, the PDF decay is faster than for the Gaussian distribution. For example, for a uniform distribution, the Gaussian deviation always has the numerical value $1.8 - 3 = -1.2$.
$\text{Example 2:}$ The first central moments of a Gaussian random variable with standard deviation $σ = 1/2$ ⇒ varince $σ^2 = 1/4$ are:
- $$\mu_2 = \frac{1}{4}, \hspace{0.4cm}\mu_4 = \frac{3}{16},\hspace{0.4cm}\mu_6 = \frac{15}{64}, \hspace{0.4cm}\mu_8 = \frac{105}{256}.$$
All central moments with odd index are identically zero.
The interactive HTML5/JavaScript applet "PDF, CDF and moments of special distributions" gives, among other things, the characteristics of the Gaussian distribution.
Gaussian generation by addition method
This simple procedure, based on the central limit theorem of statistics for the computational generation of a Gaussian random variable, shall be outlined here only in a bullet point fashion:
(1) One assumes $($between $0$ and $1)$ equally distributed and statistically independent random variables $u_i$ ⇒ mean $m_u = 1/2$, variance $\sigma_u^2 = 1/12.$
(2) One now forms the sum over $I$ summands, where $I$ must be chosen sufficiently large:
- $$s=\sum\limits_{i=1}^{I}u_i.$$
(3) According to the central limit theorem, the random variable $s$ is Gaussian distributed with good approximation if $I$ is sufficiently large. In contrast, for $I =2$ for example, only an amplitude-limited triangle PDF $($with values between $0$ and $2)$ results ⇒ convolution of two rectangles.
(4) Thus, the mean of the random variable $s$ is $m_s = I/2$. Since the uniformly distributed random variables $u_i$ were assumed to be statistically independent of each other, their variances can also be added, yielding for the variance of $s$ the value $\sigma_s^2 = I/12$.
(5) If a Gaussian distributed random variable $x$ with different mean $m_x$ and different standard deviation $σ_x$ is to be generated, the following linear transformation must still be performed:
- $$x=m_x+\frac{\sigma_x}{\sqrt{I/\rm 12}}\cdot \bigg[\big (\sum\limits_{\it i=\rm 1}^{\it I}u_i\big )-{I}/{\rm 2}\bigg].$$
(6) With the parameter $I =12$ the generation rule simplifies, which can be exploited especially in computationally time-critical applications, e.g. in a real-time simulation:
- $$x=m_x+\sigma_x\cdot \left [\big(\sum\limits_{i=\rm 1}^{12}\it u_i \rm \big )-\rm 6 \right ].$$
$\text{Conclusion:}$ However, the Gaussian random variable approximated by the addition method $($with parameter $I)$ yields values only in a limited range around the mean $m_x$. In general:
- $$m_x-\sqrt{3 I}\cdot \sigma_x\le x \le m_x+\sqrt{3 I}\cdot \sigma_x.$$
- The error with respect to the theoretical Gaussian distribution is largest at these limits and becomes smaller for increasing $I$.
- The topic of this chapter is illustrated with examples in the (German language) learning video
"Prinzip der Additionsmethode" $\Rightarrow$ "Principle of the addition method".
Gaussian generation with the Box/Muller method
In this method, two statistically independent Gaussian distributed random variables $x$ and $y$ are generated (approximately) from the two $($between $0$ and $1$ uniformlyly distributed and statistically independent random variables $u$ and $v)$ by nonlinear transformation:
- $$x=m_x+\sigma_{x}\cdot \cos(2 \pi u)\cdot\sqrt{-2\cdot \ln(v)},$$
- $$y=m_y+\sigma_{y}\cdot \sin(2 \pi u)\cdot\sqrt{-2\cdot \ln(v)}.$$
The Box and Muller method – hereafter abbreviated to "BM" – can be characterized as follows:
- The theoretical background for the validity of above generation rules is based on the regularities for two-dimensional random variables.
- Obvious equations successively yield two Gaussian values without statistical bindings. This fact can be used to reduce simulation time by generating a tuple $(x, \ y)$ of Gaussian values at each function call.
- A comparison of the computation times shows that – with the best possible implementation in each case – the BM method is superior to the addition method with $I =12$ by (approximately) a factor of $3$.
- The range of values is less limited in the BM method than in the addition method, so that even small probabilities are simulated more accurately. But even with the BM method, it is not possible to simulate arbitrarily small error probabilities.
$\text{Example 3:}$ For the following estimation, we assume the parameters $m_x = m_y = 0$ and $σ_x = σ_y = 1$.
- For a 32-bit calculator, the smallest float number that can be represented is $2^{-31} ≈ 0.466 - 10^{-9}$. Thus, the maximum value of the root expression in the generation rule of the BM method cannot become larger than approximately $6.55$ and is also extremely improbable.
- Since both the cosine and sine functions are limited in amount to $1$, this would also be the maximum possible value for $x$ and $y$.
However, an in [ES96][1] documented simulation over $10^{9}$ samples has shown that the BM method approximates the Q function very well only up to error probabilities of $10^{-5}$ but then the curve shape breaks off steeply.
- The maximum occurring value of the root expression was not $6.55$, but due to the current random variables $u$ and $v$ only about $4.6$, which explains the abrupt drop from about $10^{-5}$ on.
- Of course, this method works much better with 64 bit arithmetic operations
.
Gaussian generation with the "Tabulated Inversion" method
In this method developed by Peter Eck and Günter Söder [ES96][1] the following procedure is followed:
(1) The Gaussian PDF is divided into $J$ intervals with equal area contents – and correspondingly different widths – where $J$ represents a power of two.
(2) A characteristic value $C_j$ is assigned to the interval with index $j$. Thus, for each new function value, it is sufficient to call only one integer number generator, which will generate the integer values $j = ±1, \hspace{0.1cm}\text{...} \hspace{0.1cm}, ±J/2$ with equal probability and thus selects one of the $C_j$.
(3) If $J$ is chosen sufficiently large, e.g. $J = 2^{15} = 32\hspace{0.03cm}768$, then the $C_j$ can be set equal to the interval averages for simplicity. These values need to be calculated only once and can be stored in a file before the actual simulation.
(4) On the other hand, the boundary regions are problematic and must be treated separately. By means of nonlinear transformation a float value is determined for this according to the outliers of the Gaussian PDF.
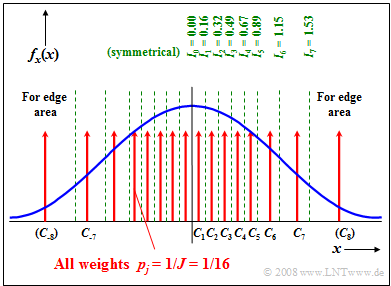
$\text{Example 4:}$ The sketch shows the PDF splitting for $J = 16$ by the boundaries $I_{-7}$, ... , $ I_7$.
- These interval boundaries were chosen so that each interval has the same area $p_j = 1/J = 1/16$ .
- The characteristic value $C_j$ of each interval lies exactly midway between $I_{j-1}$ and $I_j$.
One now generates an equally distributed discrete random variable $k$ $($with values between $1$ and $8)$ and additionally a sign bit.
- For example, if the sign bit is negative and $k =4$ the following value is output:
- $$C_{-4} = -C_4 =-(0.49+0.67)/2 =-0.58.$$
- For $k =8$ the special case occurs that one must determine the random value $C_8$ by nonlinear transformation corresponding to the outliers of the Gaussian curve.
$\text{Conclusion:}$ The "Tabulated Inversion" properties can be summarized as follows:
- This method is with $J = 2^{15}$ faster about a factor of $8$ than the BM method, with comparable simulation accuracy.
- Disadvantageous is that now the exceedance probability ${\rm Pr}(x > r)$ is no longer continuous in the inner regions,
but a staircase curve results due to the discretization. This shortcoming can be compensated by a larger $J$. - The special treatment of the edges makes the method suitable for very small error probabilities.
Exercises for the chapter
Exercise 3.6Z: Examination Correction
Exercise 3.7: Bit Error Rate (BER)
Exercise 3.7Z: Error Performance
References