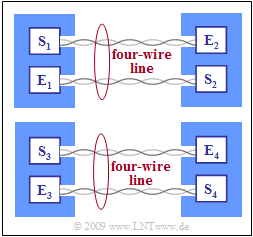
Exercise 4.8: Near-end and Far-end Crosstalk Disorders

Local and long-distance crosstalk

On the $S_0$ bus at $\rm ISDN$ ("Integrated Services Digital Networks"), data is transmitted separately according to transmission direction on a star quad. The received signal of an ISDN device is therefore disturbed not only by connections on other wires but also by crosstalk from its own transmitted signal.

In this exercise, two ISDN terminals with $\text{50 m}$ distance are considered, assuming:

For the power spectral density $\rm (PDS)$ of the transmitter of each terminal, let ${\it\Phi}_{0} = 5 \cdot 10^{-9} \ \rm W/Hz$ be very simplified:

$${\it\Phi}_{s}(f)= \left\{ \begin{array}{c} {\it\Phi}_{0} \\ 0 \end{array} \right. \begin{array}{c} {\rm{for}} \\ {\rm{for}} \end{array}\begin{array}{*{20}c} { |f| \le f_0 = 100\:{\rm kHz} \hspace{0.05cm},} \\ { |f| > f_0\hspace{0.05cm}.} \end{array}$$

The power transfer function on the $S_0$ bus $\text{(0.6 mm}$ copper two–wire line, $\text{50 m)}$ is to be approximated in the considered range $0 < |f| < 100 \ \rm kHz$ as follows (very simplified):

$$|H_{\rm K}(f)|^2 = 0.9 - 0.04 \cdot \frac{|f|}{\rm 1 \ MHz}\hspace{0.05cm}.$$

The near–end crosstalk power transfer function is given as follows $(\rm NEXT$ stands for "near–end crosstalk"$)$:

$$|H_{\rm NEXT}(f)|^2 = \left ( K_{\rm NEXT} \cdot |f|\right )^{3/2}\hspace{0.05cm},\hspace{0.2cm}K_{\rm NEXT} = 6 \cdot 10^{-10}\,{\rm s} \hspace{0.05cm}.$$

The diagram shows the system configuration under consideration.

Two twisted pairs connect subscribers $1$ and $2$ (one in each direction),
while on two other twisted pairs (not in the same star quad) there is a connection between subscriber $3$ and subscriber $4$.

Notes:

The exercise belongs to the chapter Properties of Balanced Copper Pairs.
It also refers to the chapter ISDN Basic Access in the book "Examples of Communication Systems".

Questions

	Transmitter $S_1$ leads to near-end crosstalk at receiver $E_2$.
	Transmitter $S_2$ leads to near-end crosstalk at receiver $E_2$.
	Transmitter $S_3$ leads to near-end crosstalk at receiver $E_2$.
	Near-end crosstalk is more unpleasant than far-end crosstalk.

$P_{\rm S} \ = \ $

$\ \rm mW$

$P_{\rm E} \ = \ $

$\ \rm mW$

$P_\text{NEXT} \ = \ $

$\ \rm nW$

$\rm 10 \cdot \ lg\ {\it P}_E/{\it P}_\text{NEXT} \ = \ $

$\ \rm dB$

Solution

(1) Crosstalk is caused by coupling of the transmitted signals to adjacent pairs of wires.

In the case of near–end crosstalk $\rm (NEXT)$, the interfering transmitter and the interfered receiver are at the same end of the line.
In the case of far–end crosstalk $\rm (FEXT)$, they are at different ends.
However, since the interfering signals are also very strongly attenuated on the copper wire pair, NEXT is always by far the more dominant interfering effect compared with FEXT.

Solutions 2 and 4 are correct:

Here, the receiver $E_2$ is particularly disturbed by its own transmitter $S_2$, i.e. by near–end crosstalk.
The interference of $E_2$ by $S_3$ is far–end crosstalk, while $S_1$ provides the useful signal for $E_2$.

(2) The transmit power is equal to the integral over the power spectral density:

$$P_{\rm S} = {\it\Phi}_{0} \cdot 2 f_0 = 5 \cdot 10^{-9}\, {\rm W}/{\rm Hz} \cdot 2 \cdot 10^{5}\,{\rm Hz}\hspace{0.15cm}\underline{ = 1\,{\rm mW}} \hspace{0.05cm}.$$

(3) The following applies to the received power (excluding the component due to near–end crosstalk):

$$P_{\rm E} = \int_{-\infty}^{ +\infty} {\it\Phi}_{s}(f) \cdot |H_{\rm K}(f)|^2 \hspace{0.1cm}{\rm d}f = 2 {\it\Phi}_{0} \cdot \int_{0}^{ f_0} \left [ 0.9 - 0.04 \cdot \frac{f}{f_0} \right ] \hspace{0.1cm}{\rm d}f $$

$$\Rightarrow \hspace{0.3cm}P_{\rm E} = 2 {\it\Phi}_{0} \cdot \left [ 0.9 \cdot f_0 - \frac{0.04}{2} \cdot \frac{f_0^2}{f_0} \right ] = 2 {\it\Phi}_{0} \cdot 0.88 = 0.88 \cdot P_{\rm S}\hspace{0.15cm}\underline{ = 0.88 \,{\rm mW}} \hspace{0.05cm}.$$

(4) For the interfering power component of the crosstalk interference one obtains

$$P_{\rm NEXT} = \int_{-\infty}^{ +\infty} {\it\Phi}_{s}(f) \cdot |H_{\rm NEXT}(f)|^2 \hspace{0.1cm}{\rm d}f = 2 {\it\Phi}_{0} \cdot {K_{\rm NEXT}\hspace{0.01cm}}^{3/2} \cdot \int_{0}^{ f_0} f^{3/2} \hspace{0.1cm}{\rm d}f $$

$$\Rightarrow \hspace{0.3cm} P_{\rm NEXT} = \frac{4}{5} \cdot {\it\Phi}_{0} \cdot {K_{\rm NEXT}\hspace{0.01cm}}^{3/2} \cdot f_0^{5/2} = 0.8 \cdot 5 \cdot 10^{-9}\, \frac{\rm W}{\rm Hz} \cdot \left ( 6 \cdot 10^{-10}\,{\rm s}\right )^{3/2} \cdot \left ( 10^{5}\,{\rm Hz}\right )^{5/2} = {0.186 \cdot 10^{-9}\,{\rm W}} \hspace{0.05cm} = \hspace{0.15cm}\underline{0.186 \,{\rm nW}} \hspace{0.05cm}.$$

(5) ${P_{\rm E}}/{P_{\rm NEXT}} \approx 4.73 \cdot 10^{6}$ is valid, resulting in the logarithmic value of

$$10 \cdot {\rm lg}\hspace{0.15cm} {P_{\rm E}}/{P_{\rm NEXT}} = 10 \cdot {\rm lg}\hspace{0.15cm} (4.73 \cdot 10^{6}) \hspace{0.15cm}\underline{= 66.7\,\,{\rm dB}} \hspace{0.05cm}.$$