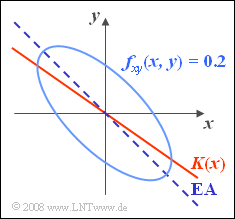
Exercise 4.4Z: Contour Lines of the "2D-PDF"

Gaussian 2D–PDF: Contour lines

Given a two-dimensional Gaussian random variable $(x, y)$ with mean $(0, 0)$ and the 2D–PDF

$$f_{xy}(x,\ y) = C\cdot{\rm e}^{-(x^{\rm 2} + y^{\rm 2} +\sqrt{\rm 2}\hspace{0.05cm}\cdot \hspace{0.05cm} x \hspace{0.05cm}\cdot \hspace{0.05cm} y)}.$$

It is further known that the standard deviations are $\sigma_x=\sigma_y=1.$

Entered in the sketch are:

a contour line of this PDF for $f_{xy}(x,y) =0.2$,
the (dark blue) ellipse major axis $\rm (EA)$, and
the (red) correlation line $y=K\cdot x$.

Hints:

The exercise belongs to the chapter Two-dimensional Gaussian Random Variables.
More information on this topic is provided in the (German language) learning video "Gaußsche 2D-Zufallsgrößen":

Part 1: Gaussian random variables without statistical bindings,

Part 2: Gaussian random variables with statistical bindings.

Questions

$\rho_{xy} \ = \ $

$C \ = \ $

$\alpha\ = \ $

$ \ \rm degrees$

$x_0/y_0 \ = \ $

	The correlation line is steeper than the ellipse major axis.
	The angle ofthe correlation line with respect to the $x$–axis is about $-35^\circ$.
	The correlation line intersects all contour line where a vertical tangent can be applied to the ellipse.

Solution

(1) Even without specifying $\sigma_x = \sigma_y = 1$ one could see that the standard deviations $\sigma_x$ and $\sigma_y$ are equal,

since in the exponent of $f_{xy}(x, y)$ the coefficients at $x^2$ and $y^2$ are equal.
By comparing coefficients, we thus obtain:

$$\frac{- 2 \rho_{xy}}{\sigma_x\cdot\sigma_y} = \sqrt{2}\hspace{0.3cm}\Rightarrow\hspace{0.3cm} \rho_{xy}=\frac{-1}{\sqrt{2}} \hspace{0.15cm}\underline{\approx -0.707}.$$

(2) Using the numerical values calculated in point (1) we also obtain:

$$C=\frac{\rm 1}{\rm 2\it\pi\cdot\sigma_x\cdot\sigma_y\cdot\sqrt{\rm 1 - \rho_{xy}^{\rm 2}}} =\frac{\rm 1}{\rm 2\pi\cdot\rm 1\cdot 1\cdot\sqrt{0.5}}=\frac{\rm 1}{\sqrt{\rm 2}\cdot \pi}\hspace{0.15cm}\underline{\approx \rm 0.225}.$$

(3) The general equation is:

$$\alpha = {\rm 1}/{\rm 2}\cdot \rm arctan \ (\rm 2 \cdot\it \rho_{xy}\cdot \frac{\sigma_x\cdot\sigma_y}{\sigma_x^{\rm 2} - \sigma_y^{\rm 2}}{\rm ).}.$$

Applies $\sigma_x = \sigma_y$ and $\rho_{xy} \ne 0$, then the angle is always $\alpha = \pm 45^\circ$, where the sign is equal to the sign of $\rho_{xy}$ .
In the present case $\alpha\hspace{0.15cm}\underline{ = -45^\circ}$ holds.

(4) For the plotted contour line holds:

$$f_{xy}(x, y)=\frac{1}{\sqrt{2}\cdot \pi}\cdot {\rm e}^{(x^{2} + y^{2} + \sqrt{2}\hspace{0.05cm}\cdot \hspace{0.05cm} x \hspace{0.05cm}\cdot \hspace{0.05cm}y)}=0.2\hspace{0.3cm} \rightarrow \hspace{0.3cm}{\rm e}^{-(x^{2} + y^{2} + \sqrt{2}\hspace{0.05cm} \cdot \hspace{0.05cm} x \hspace{0.05cm} \cdot \hspace{0.05cm}y)} = 0.8885 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} x^{\rm 2} + y^{\rm 2} + \sqrt{\rm 2}\cdot\hspace{0.05cm} x \hspace{0.05cm} \cdot \hspace{0.05cm}y = -{\rm ln(0.8885)} \approx\rm 0.118.$$

The angle of the ellipse major axis is $\alpha = -45^\circ$. Therefore $y_0 = - x_0$ must hold. It further follows:

$$x_{\rm 0}^{\rm 2} + (-x_{\rm 0})^{\rm 2} + \sqrt{\rm 2}\cdot x_{\rm 0}(-x_{\rm 0}) = 0.118$$

$$\Rightarrow \hspace{0.3cm}(\rm 2 - \sqrt{\rm 2})\cdot \it x_{\rm 0}^{\rm 2} = {\rm 0.118} \hspace{0.5cm}\rightarrow \hspace{0.5cm} x_{\rm 0}^{\rm 2} \approx \frac{\rm0.118}{\rm0.585}\approx\rm 0.202; \hspace{0.5cm} {\it x}_{\rm 0}\approx\pm\rm 0.450.$$

The two intersections of the plotted contour lines with the ellipse major axis are thus at $(+0.45, -0.45)$ and $(-0.45, +0.45)$.
The quotient in both cases is $x_0/y_0 \hspace{0.15cm}\underline{ = -1}$.

(5) Correct are the proposed solutions 2 and 3:

With $\sigma_x = \sigma_y$ and the result of the subtask (1) holds for the angle of the correlation line:

$$\theta_{y\hspace{0.05cm}\rightarrow \hspace{0.05cm}x} = \arctan (\rho_{\it xy})=\arctan(-{\rm 1}/{\sqrt{\rm 2}})\approx -\rm 35.3^{\circ}.$$

This means: The first statement is false and the second is true.

The following is the proof of the correctness of the last statement:

Solving the elliptic equation $($with $z = 0. 118)$, so $x^{\rm 2}+ y^{\rm 2} +\sqrt{\rm 2}\cdot \it x\cdot \it y - \it z = \rm 0$, to $y$ we get after solving a quadratic equation:

$$y_{\rm 1, \ 2}={\sqrt{\rm 2}}/ {\rm 2} \cdot x\pm\sqrt{{x^{\rm 2}}/{\rm 2}-x^{\rm 2}+{\it z}} \hspace{0.5cm}\rightarrow \hspace{0.5cm} y_{\rm 1, \ 2}={\it x}/{\sqrt{\rm 2}}\pm \sqrt{z-{x^{\rm 2}}/{\rm 2}}.$$

The vertical tangent results for the case that the two solutions $y_{\rm 1, \rm 2}$ are identical. That is: The root expression must result in zero.
The solution for positive $x$ is then: $x_{\rm T}=\sqrt{\rm 2\cdot \it z}=\rm \rm 0.485.$
Inserted into the ellipse equation one obtains für the $y$–value of the tangent point:

$$x_{\rm T}^{\rm 2} + y_{\rm T}^{\rm 2} + \sqrt{2} \cdot x_{\rm T} \cdot y_{\rm T} - z = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} 2 z + y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot y_{\rm T} - z = 0$$

$$\Rightarrow \hspace{0.3cm}y_{\rm T}^{\rm 2} + 2\sqrt{ z}\cdot y_{\rm T} + z = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (y_{\rm T} + \sqrt{ z}) = 0\hspace{0.5cm}\Rightarrow \hspace{0.5cm} y_{\rm T} = -\sqrt{ z} = -0.343.$$

This gives $y_{\rm T}=-{x_{\rm T}}/{\sqrt{\rm 2}}. $ But this also means: The tangent point $(x_{\rm T}, y_{\rm T})$ lies exactly on the correlation line $y=K(x)=-{ x}/{\sqrt{\rm 2}}.$