Exercise 4.8: Diamond-shaped Joint PDF

• Return to book

Diamond shaped joint PDF

We consider a two-dimensional random variable  $(x,\hspace{0.08cm} y)$  whose components arise as linear combinations of two random variables  $u$  and  $v$:

$$x=2u-2v+1,$$

$$y=u+3v.$$

Further,  note:

• The two statistically independent random variables  $u$  and  $v$  are each uniformly distributed between  $0$  and  $1$.
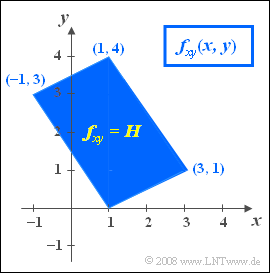
• In the figure you can see the joint PDF.  Within the parallelogram drawn in blue holds:

$$f_{xy}(x,\hspace{0.08cm} y) = H = {\rm const.}$$

• Outside the parallelogram no values are possible:  $f_{xy}(x,\hspace{0.08cm} y) = 0$.

Hints:

• The exercise belongs to the chapter  Linear_Combinations of Random Variables.
• Reference is also made to the page  Regression line.
• We also refer here to the interactive applet  Correlation coefficient and regression line
• Assume - if possible - the given equations.  Use the information of the above sketch mainly only to check your results.

Questions

1

Wie groß ist die Höhe  $H$  der 2D–WDF innerhalb des Parallelogramms?

$H \ = \ $

2

Welche Werte von  $u$  und  $v$  liegen dem Eckpunkt  $(-1, 3)$  zugrunde?

$u \ = \ $

$v \ = \ $

3

Berechnen Sie den Korrelationskoeffizienten  $\rho_{xy}$.

$\rho_{xy}\ = \ $

4

Wie lautet die Korrelationsgerade  $y=K(x)$?  Bei welchem Punkt  $y_0$  schneidet diese die  $y$-Achse?

$y_0\ = \ $

5

Berechnen Sie die Randwahrscheinlichkeitsdichtefunktion $f_x(x)$.  Wie groß ist die Wahrscheinlichkeit, dass die Zufallsgröße  $x$  negativ ist?

${\rm Pr}(x < 0)\ = \ $

6

Berechnen Sie die Randwahrscheinlichkeitsdichtefunktion $f_y(y)$.  Wie groß ist die Wahrscheinlichkeit, dass die Zufallsgröße  $y >3$  ist?

${\rm Pr}(y > 3)\ = \ $

Musterlösung

Solution

(1)  Die Fläche des Parallelogramms kann aus zwei gleich großen Dreiecken zusammengesetzt werden.

• Die Fläche des Dreiecks  $(1,0)\ (1,4)\ (-1,3)$  ergibt  $0.5 · 4 · 2 = 4$.
• Die Gesamtfläche ist doppelt so groß:   $F = 8$.
• Da das WDF–Volumen stets  $1$  ist, gilt  $H= 1/F\hspace{0.15cm}\underline{ = 0.125}$.

(2)  Der minimale Wert von  $x$  ergibt sich für  $\underline{ u=0}$  und  $\underline{ v=1}$.

• Daraus folgen aus obigen Gleichungen die Ergebnisse  $x= -1$  und  $y= +3$.

(3)  Die im Theorieteil angegebene Gleichung gilt allgemein, also für jede beliebige WDF der beiden statistisch unabhängigen Größen  $u$  und  $v$,

• so lange diese gleiche Streuungen aufweisen  $(\sigma_u = \sigma_v)$.

• Mit  $A = 2$,  $B = -2$,  $D = 1$  und  $E = 3$  erhält man:

$$\rho_{xy } = \frac {\it A \cdot D + B \cdot E}{\sqrt{(\it A^{\rm 2}+\it B^{\rm 2})(\it D^{\rm 2}+\it E^{\rm 2})}} =\frac {2 \cdot 1 -2 \cdot 3}{\sqrt{(4 +4)(1+9)}} = \frac {-4}{\sqrt{80}} = \frac {-1}{\sqrt{5}}\hspace{0.15cm}\underline{ = -0.447}. $$

(4)  Die Korrelationsgerade lautet allgemein:

$$y=K(x)=\frac{\sigma_y}{\sigma_x}\cdot\rho_{xy}\cdot(x-m_x)+m_y.$$

• Aus den linearen Mittelwerten  $m_u = m_v = 0.5$  und den in der Aufgabenstellung angegebenen Gleichungen erhält man  $m_x = 1$  und  $m_y = 2$.

• Die Varianzen von  $u$  und  $v$  betragen jeweils  $\sigma_u^2 = \sigma_v^2 =1/12$.  Daraus folgt:

$$\sigma_x^2 = 4 \cdot \sigma_u^2 + 4 \cdot \sigma_v^2 = 2/3,$$

$$\sigma_y^2 = \sigma_u^2 + 9\cdot \sigma_v^2 = 5/6.$$

• Setzt man diese Werte in die Gleichung der Korrelationsgeraden ein, so ergibt sich:

$$y=K(x)=\frac{\sqrt{5/6}}{\sqrt{2/3}}\cdot (\frac{-1}{\sqrt{5}})\cdot(x-1)+2= - x/{2} + 2.5.$$

• Daraus folgt der Wert  $y_0=K(x=0)\hspace{0.15cm}\underline{ = 2.5}$

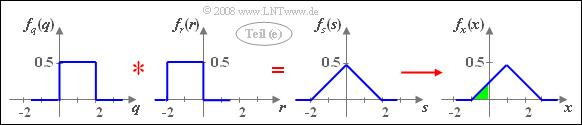
(5)  Mit den Hilfsgrößen   $q= 2u$,   $r= -2v$   und   $s= x-1$  gilt der Zusammenhang:   $s= q+r$.

• Da  $u$  und  $v$  jeweils zwischen  $0$  und  $1$  gleichverteilt sind, besitzt  $q$  eine Gleichverteilung im Bereich von  $0$  bis  $2$  und  $r$  ist gleichverteilt zwischen  $-2$  und  $0$.

• Da zudem  $q$  und  $r$  nicht statistisch voneinander abhängen, gilt für die WDF der Summe:

Dreieckförmige WDF $f_x(x)$

$$f_s(s) = f_q(q) \star f_r(r).$$

• Die Addition  $x = s+1$  führt zu einer Verschiebung der Dreieck–WDF um  $1$  nach rechts.
• Für die gesuchte Wahrscheinlichkeit  (im folgenden Bild grün hinterlegt)  gilt deshalb:   ${\rm Pr}(x < 0)\hspace{0.15cm}\underline{ = 0.125}$.

Trapezförmige WDF $f_y(y)$

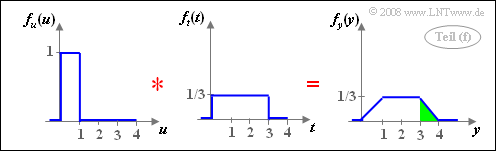
(6)  Analog zur Musterlösung für die Teilaufgabe  (5)  gilt mit  $t = 3v$:

$$f_y(y) = f_u(u) \star f_t(t).$$

• Die Faltung zwischen zwei verschieden breiten Rechtecken ergibt ein Trapez.
• Für die gesuchte Wahrscheinlichkeit erhält man  ${\rm Pr}(y>3) =1/6\hspace{0.15cm}\underline{ \approx 0.167}$.
• Diese Wahrscheinlichkeit ist in der rechten Skizze grün hinterlegt.