Auto-Correlation Function

1 Random processes
2 Stationary random processes
3 Ergodic random processes
4 Generally valid description of random processes
5 General definition of the autocorrelation function
6 ACF for ergodic processes
7 Eigenschaften der Autokorrelationsfunktion
8 Interpretation der Autokorrelationsfunktion
9 Numerische AKF-Ermittlung
10 Genauigkeit der numerischen AKF-Berechnung
11 Aufgaben zum Kapitel

Random processes

An important concept in stochastic signal theory is the random process. Below are some characteristics of such a stochastic process - these terms are used synonymously both in the literature and in our tutorial.

$\text{Definitions:}$ By a random process $\{x_i(t)\}$ we understand a mathematical model for an ensemble of (many) random signals, which can and will differ from each other in detail, but nevertheless have certain common properties.

To describe a random process $\{x_i(t)\}$ we start from the notion that there are any number of random generators, completely identical in their physical and statistical properties, each of which yields a random signal $x_i(t)$ .
Each random generator, despite having the same physical realization, outputs a different time signal $x_i(t)$ that exists for all times from $-∞$ to $+∞$ This specific random signal is called the $i$-th pattern signal.
Every random process involves at least one stochastic component - for example, the amplitude, frequency, or phase of a message signal - and therefore cannot be accurately predicted by an observer.
The random process differs from the usual random experiments in probability or statistics in that the result is not an event but a function (time signal).
If we consider the random process $\{x_i(t)\}$ at a fixed time, we return to the simpler model from the chapter From Random Experiment to Random Variable, according to which the experimental result is an event that can be assigned to a random variable

.

These statements are now illustrated by the example of a binary random generator, which - at least in thought - can be realized arbitrarily often.

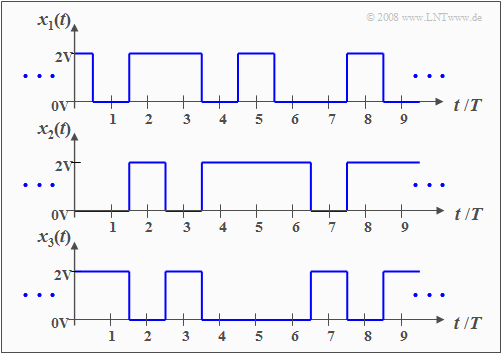
$\text{Example 1:}$ The graph shows three different pattern signals of a random process with the following properties:

To define a random process

The random process here $\{x_i(t)\}$ consists of an ensemble of rectangular pattern functions, which can be described as follows:

$$x_i(t)=\sum^{+\infty}_{\nu=-\infty} (a_\nu)_i\cdot g(t-\nu \cdot T ).$$

The fundamental momentum $g(t)$ has in the range from $-T/2$ to $+T/2$ the value $2\hspace{0.03cm}\rm V$; outside it is zero and exactly at $\pm T/2$ only half as large $(1\hspace{0.03cm}\rm V)$.
Remember: A pulse, as defined in the chapter Signal Classification in the book "Signal Representation", is both a deterministic and energy-limited signal.
The statistics of the random process under consideration is due solely to the dimensionless amplitude coefficients $(a_ν)_i ∈ \{0, 1\}$ which are time-indexed $ν$ for the $i$-th pattern function.
Despite the different signal courses in detail, the sketched signals $x_1(t)$, $x_2(t)$, $x_3(t)$ and also all further pattern signals $x_4(t)$, $x_5(t)$, $x_6(t)$, ... have certain common features, which will be elaborated in the following.

Stationary random processes

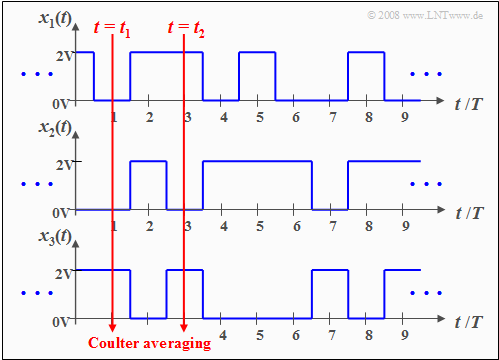
If one defines the instantaneous value of all pattern functions $x_i(t)$ at a fixed time $t = t_1$ as a new random variable $x_1 = \{ x_i(t_1)\}$, its statistical properties can be described according to the statements

On the definition of stationary random processes

of the second chapter "Discrete Random Variables" and
of the third chapter "Continuous Random Variables"

in this book.

Similarly, for the time of observation $t = t_2$ we obtain the random variable $x_2 = \{ x_i(t_2)\}$.

Note on nomenclature: Note that.

$x_1(t)$ and $x_2(t)$ are sample functions of the random process $\{x_i(t)\}$ ,
while the random variables $x_1$ and $x_2$ characterize the whole process at times $t_1$ and $t_2$ respectively.

The calculation of the statistical characteristics must be done by coulter averaging over all possible pattern functions $($averaging over the run variable $i$, i.e. over all realizations$)$.

$\text{Definition:}$

For a stationary random process $\{x_i(t)\}$ all statistical parameters $($mean, standard deviation, higher order moments, probabilities of occurrence, etc. $)$ of the random variables $x_1 = \{ x_i(t_1)\}$ and $x_2 = \{ x_i(t_2)\}$ are equal.
Also at other times, the values are exactly the same.

The converse is One calls a random process $\{x_i(t)\}$ a non-stationary if it has different statistical properties at different times.

$\text{Example 2:}$ A large number of measuring stations at the equator determine the temperature daily at 12 o'clock local time. If one averages over all these measured values, one can eliminate the influence of local indicators (e.g. Gulf Stream). If one plots the mean values (coulter averaging) over time, almost a constant will result, and one can speak of a stationary process .

A comparable series of measurements at 50° latitude would indicate a non-stationary process due to the seasonal variations, with significant differences in mean and variance of the noon temperature between January and July.

Ergodic random processes

An important subclass of stationary random processes are the so-called ergodic processes with the following properties:

$\text{Definition:}$ In an ergodic process $\{x_i(t)\}$ each individual pattern function $x_i(t)$ is representative of the entire ensemble.

All statistical descriptive quantities of an ergodic process can be obtained from a single pattern function by time averaging $($referring to the running variables $ν = t/T$ ⇒ normalized time$)$ .
This also means that With ergodicity, the time averages of each sample function coincide with the corresponding coulter averages at arbitrary time points $ν$.

On the definition of ergodic random processes

For example, with ergodicity, for the moment $k$-th order:

$$m_k=\overline{x^k(t)}={\rm E}\big[x^k\big].$$

Here, the sweeping line denotes the time mean, while the coulter mean is to be determined by expected value generation $\rm E\big[ \hspace{0.1cm}\text{...} \hspace{0.1cm} \big]$ as described in chapter Moments of a discrete random variable .

Note: Ergodicity cannot be proved from a finite number of pattern functions and finite signal sections.

However, ergodicity is hypothetically - but nevertheless quite justifiably - assumed in most applications.
On the basis of the results found, the plausibility of this ergodicity hypothesis' must subsequently be checked.

Generally valid description of random processes

If the random process to be analyzed $\{x_i(t)\}$ is not stationary and thus certainly not ergodic, the moments must always be determined as coulter averages. In general, these are time-dependent:

$$m_k(t_1) \ne m_k(t_2).$$

However, since by the moments also the characteristic function (Fourier retransform of the PDF).

$$ C_x(\Omega) ={\rm\sum^{\infty}_{{\it k}=0}}\ \frac{m_k}{k!}\cdot \Omega^{k}\ \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\,\ f_{x}(x)$$

is fixed, the probability density function $f_{x}(x)$ is also time dependent.

If not only the amplitude distributions at different times $t_1, t_2$, ... are to be determined, but also the statistical bindings between the signal values at these times, one has to pass to the joint probability density function .

For example, considering the two time points $t_1$ and $t_2$, note the following:

The 2D PDF is obtained according to the specifications on page properties and examples of two-dimensional random variables with $x = x(t_1)$ and $y = x(t_2)$. It is obvious that already the determination of this quantity is very complex.
If one further considers that to capture all statistical bindings within the random process actually the $n$-dimensional composite probability density function (joint PDF) would have to be used, where if possible the limit $n → ∞$ still has to be formed, one recognizes the difficulties for the solution of practical problems.
For these reasons, in order to describe the statistical bindings of a random process, one proceeds to the autocorrelation function, which simplifies the problem. This is first defined in the following section for the general case.

General definition of the autocorrelation function

$\text{Allgemeingültige Definition:}$ Die Autokorrelationsfunktion (AKF) eines Zufallsprozesses $\{x_i(t)\}$ ist gleich dem Erwartungswert des Produkts der Signalwerte zu zwei Zeitpunkten $t_1$ und $t_2$:

$$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big].$$

Diese Definition gilt unabhängig davon, ob der Zufallsprozess ergodisch oder nichtergodisch ist, und sie gilt im Prinzip auch für nichtstationäre Prozesse.

Hinweis zur Nomenklatur:

Um den Zusammenhang mit der Kreuzkorrelationsfunktion $φ_{xy}$ zwischen den beiden statistischen Größen $x$ und $y$ deutlich zu machen, wird in mancher Literatur für die Autokorrelationsfunktion anstelle von $φ_{x}$ auch häufig die Schreibweise $φ_{xx}$ verwendet. In unserem Lerntutorial verzichten wir darauf.

Ein Vergleich mit dem Abschnitt Erwartungswerte zweidimensionaler Zufallsgrößen zeigt, dass der AKF–Wert $φ_x(t_1, t_2)$ das gemeinsame Moment $m_{11}$ zwischen den beiden Zufallsgrößen $x(t_1)$ und $x(t_2)$ angibt.

Während für exakte Aussagen hinsichtlich der statistischen Bindungen eines Zufallsprozesses eigentlich die $n$–dimensionale Verbunddichte $($mit $n → ∞)$ benötigt wird, werden durch den Übergang auf die Autokorrelationsfunktion implizit folgende Vereinfachungen getroffen:

Anstelle von unendlich vielen Zeitpunkten werden hier nur zwei betrachtet, und anstelle aller Momente $m_{\hspace{0.05cm}k\hspace{0.05cm}l}$ zu den beiden Zeitpunkten $t_1$ und $t_2$ mit $k, \ l ∈ \{1, 2, 3, \text{...} \}$ wird hier nur das gemeinsame Moment $m_{11}$ erfasst.
Das Moment $m_{11}$ gibt ausschließlich die lineare Abhängigkeit ("Korrelation") des Prozesses wieder. Alle statistische Bindungen höherer Ordnung werden dagegen nicht berücksichtigt.
Deshalb sollte bei der Bewertung von Zufallsprozessen mittels AKF stets berücksichtigt werden, dass diese nur sehr beschränkte Aussagen über die statistischen Bindungen allgemein erlaubt.

$\text{Beispiel 3:}$ Die obige Definition der Autokorrelationsfunktion gilt allgemein, also auch für nichtstationäre und nichtergodische Prozesse.

Ein Beispiel eines nichtstationären Vorgangs ist das Auftreten von Impulsstörungen im Fernsprechnetz, verursacht durch Wählimpulse in benachbarten Leitungen.
Bei Digitalsignalübertragung führen solche nichtstationären Störprozesse meist zu Bündelfehlern.

ACF for ergodic processes

Zur Autokorrelationsfunktion bei ergodischen Prozessen

Im Folgenden beschränken wir uns auf stationäre und ergodische Prozesse.

Ein solcher Zufallsprozess $\{x_i(t)\}$ wird zum Beispiel bei der Untersuchung von Thermischem Rauschen zugrunde gelegt. Dabei wird von der Vorstellung ausgegangen, dass

beliebig viele, in ihren physikalischen und statistischen Eigenschaften völlig gleiche Widerstände vorhanden sind,
von denen jeder ein anderes Zufallssignal $x_i(t)$ abgibt.

Die Grafik zeigt einen solchen stationären und ergodischen Prozess:

Die einzelnen Musterfunktionen $x_i(t)$ können zu allen beliebigen Zeiten alle beliebigen Werte annehmen. Das bedeutet, dass der hier betrachtete Zufallsprozess $\{x_i(t)\}$ sowohl wert– als auch zeitkontinuierlich ist.

Auch wenn über die tatsächlichen Signalwerte der einzelnen Musterfunktionen aufgrund der Stochastik keine Aussagen getroffen werden können, so sind die Momente und die WDF zu allen Zeitpunkten gleich.

In der Grafik ist aus Gründen einer verallgemeinerten Darstellung auch ein Gleichanteil $m_x$ berücksichtigt, der bei Thermischem Rauschen allerdings nicht vorhanden ist.

$\text{Definition:}$ Man spricht von einem stationären Zufallsprozess $\{x_i(t)\}$, wenn seine statistischen Eigenschaften invariant gegenüber Zeitverschiebungen sind.

Für die Autokorrelationsfunktion (AKF) bedeutet diese Aussage, dass sie nicht mehr eine Funktion der beiden unabhängigen Zeitvariablen $t_1$ und $t_2$ ist, sondern nur noch von der Zeitdifferenz $τ = t_2 - t_1$ abhängt:

$$\varphi_x(t_1,t_2)\rightarrow{\varphi_x(\tau)={\rm E}\big[x(t)\cdot x(t+\tau)\big]}.$$

Die Scharmittelung kann dabei zu jeder beliebigen Zeit $t$ erfolgen.

Unter der weiteren Annahme eines ergodischen Zufallsprozesses können alle Momente auch durch Zeitmittelung über eine einzige ausgewählte Musterfunktion $x(t)$ ermittelt werden. Alle diese Zeitmittelwerte stimmen in diesem Sonderfall mit den entsprechenden Scharmittelwerten überein.

$\text{Definition:}$ Damit folgt für die AKF eines ergodischen Zufallsprozesses, dessen Mustersignale jeweils von $–∞$ bis $+∞$ reichen $(T_{\rm M}$ bezeichnet die Messdauer$)$:

$$\varphi_x(\tau)=\overline{x(t)\cdot x(t+\tau)}=\lim_{T_{\rm M}\to\infty}\,\frac{1}{T_{\rm M} }\cdot\int^{T_{\rm M}/{\rm 2} }_{-T_{\rm M}/{\rm 2} }x(t)\cdot x(t+\tau)\,\,{\rm d}t.$$

Die überstreichende Linie kennzeichnet die Zeitmittelung über das unendlich ausgedehnte Zeitintervall.

Bei periodischen Signalen kann man auf den Grenzübergang verzichten, so dass in diesem Sonderfall die Autokorrelationsfunktion mit der Periodendauer $T_0$ auch in folgender Weise geschrieben werden kann:

$$\varphi_x(\tau)=\frac{1}{T_{\rm 0}}\cdot\int^{T_{\rm 0}/2}_{-T_{\rm 0}/2}x(t)\cdot x(t+\tau)\,\,{\rm d}t=\frac{1}{T_{\rm 0}}\cdot\int^{T_{\rm 0}}_{\rm 0}x(t)\cdot x(t+\tau)\,\,{\rm d}t .$$

Wichtig ist nur, dass insgesamt genau über eine Periodendauer $T_0$ (oder Vielfache davon) gemittelt wird. Egal ist, welchen Zeitausschnitt man verwendet.

Eigenschaften der Autokorrelationsfunktion

Hier werden wichtige Eigenschaften der Autokorrelationsfunktion (AKF) zusammengestellt, wobei wir von der ergodischen AKF–Form $φ_x(τ)$ ausgehen:

Ist der betrachtete Zufallsprozess reell, so gilt dies auch für seine Autokorrelationsfunktion.
Die AKF besitzt die Einheit einer Leistung, zum Beispiel "Watt" $\rm (W)$. Häufig bezieht man diese auf den Widerstand $1\hspace{0.03cm} Ω$; $φ_x(τ)$ hat dann die Einheit $\rm V^2$ bzw. $\rm A^2$.
Die AKF ist immer eine gerade Funktion ⇒ $φ_x(–τ) = φ_x(τ)$. Alle Phasenbeziehungen des Zufallsprozesses gehen in der AKF verloren.
Die AKF an der Stelle $τ = 0$ gibt den quadratischen Mittelwert $m_2$ (Moment zweiter Ordnung) und damit die gesamte Signalleistung (Gleich– und Wechselanteil) an:

$$\varphi_x(\tau = 0)= m_2=\overline{ x^2(t)}.$$

Das AKF–Maximum tritt stets bei $τ = 0$ auf, und es gilt: $|φ_x(τ)| ≤ φ_x(0)$. Bei nichtperiodischen Prozessen ist für $τ ≠ 0$ der Betrag $|φ_x(τ)|$ stets kleiner als $φ_x(\tau =0)$ ⇒ Leistung des Zufallsprozesses.
Bei einem periodischen Zufallsprozess weist die AKF die gleiche Periodendauer $T_0$ wie die einzelnen Mustersignale $x_i(t)$ auf:

$$\varphi_x(\pm{T_0})=\varphi_x(\pm{2\cdot T_0})= \hspace{0.1cm}\text{...} \hspace{0.1cm}= \varphi_x(0).$$

Der Gleichanteil $m_1$ eines nichtperiodischen Signals kann aus dem Grenzwert der Autokorrelationsfunktion für $τ → ∞$ berechnet werden. Hierbei gilt:

$$\lim_{\tau\to\infty}\,\varphi_x(\tau)= m_1^2=\big [\overline{ x(t)}\big]^2.$$

Dagegen schwankt bei Signalen mit periodischen Anteilen der Grenzwert der AKF für $τ → ∞$ um diesen Endwert (Quadrat des Gleichanteils).

Interpretation der Autokorrelationsfunktion

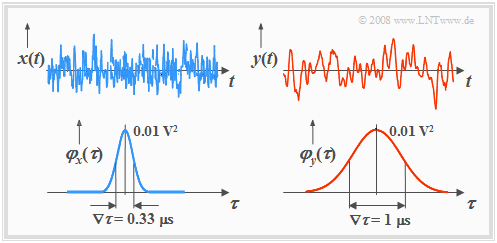
Die Grafik zeigt oben je ein Mustersignal zweier Zufallsprozesse $\{x_i(t)\}$ und $\{y_i(t)\}$, unten die zugehörigen Autokorrelationsfunktionen.

AKF von hochfrequenten und niederfrequenten Prozessen

Anhand dieser Darstellungen sind folgende Aussagen möglich:

$\{y_i(t)\}$ hat stärkere innere statistische Bindungen als $\{x_i(t)\}$. Spektral gesehen ist der Prozess $\{y_i(t)\}$ also niederfrequenter.
Die skizzierten Mustersignale $x(t)$ und $y(t)$ lassen bereits vermuten, dass beide Prozesse mittelwertfrei sind und den gleichen Effektivwert aufweisen.
Die obigen Autokorrelationsfunktionen bestätigen diese Aussagen. Die liearen Mittelwerte $m_x = m_y = 0$ ergeben sich jeweils aus dem AKF–Grenzwert für $τ → ∞$.
Wegen $m_x = 0$ gilt hier für die Varianz: $σ_x^2 = φ_x(0) = 0.01 \hspace{0.05cm} \rm V^2$, und der Effektivwert ist demzufolge $σ_x = 0.1 \hspace{0.05cm}\rm V$.
$y(t)$ hat die gleiche Varianz und und den gleichen Effektivwert wie $x(t)$. Die AKF–Werte fallen um so langsamer ab, je stärker die inneren statistischen Bindungen sind.
Das Signal $x(t)$ mit schmaler AKF ändert sich zeitlich sehr schnell, während beim niederfrequenteren Signal $y(t)$ die statistischen Bindungen deutlich weiter reichen.
Das bedeutet aber auch, dass der Signalwert $y(t + τ)$ aus $y(t)$ besser vorhergesagt werden kann als $x(t + τ)$ aus $x(t)$.

$\text{Definition:}$ Eine quantitative Kenngröße für die Stärke der statistischen Bindungen ist die äquivalente AKF-Dauer $∇τ$ (man spricht „Nabla–tau”), die sich aus der AKF über das flächengleiche Rechteck ermitteln lässt:

$${ {\rm \nabla} }\tau =\frac{1}{\varphi_x(0)}\cdot\int^{\infty}_{-\infty}\ \varphi_x(\tau)\,\,{\rm d}\tau. $$

Bei den hier betrachteten Prozessen (mit gaußähnlicher AKF) gilt entsprechend obiger Skizze: $∇τ_x = 0.33 \hspace{0.05cm} \rm µ s$ bzw. $∇τ_y = 1 \hspace{0.05cm} \rm µs$.

Als ein weiteres Maß für die Stärke der statistischen Bindungen wird in der Literatur häufig die Korrelationsdauer $T_{\rm K}$ verwendet. Diese gibt die Zeitdauer an, bei der die Autokorrelationsfunktion auf die Häfte ihres Maximalwertes abgefallen ist.

Numerische AKF-Ermittlung

Bisher haben wir stets zeitkontinuierliche Signale $x(t)$ betrachtet, die für die Darstellung und Simulation mittels Digitalrechner ungeeignet sind. Hierzu ist vielmehr eine zeitdiskrete Signaldarstellung $〈x_ν〉$ erforderlich, wie im Kapitel Zeitdiskrete Signaldarstellung unseres ersten Buches dargelegt.

Hier eine kurze Zusammenfassung:

Das zeitdiskrete Signal $〈x_ν〉$ ist die Folge der Abtastwerte $x_ν = x(ν · T_{\rm A}).$ Das zeitkontinuierliche Signal $x(t)$ wird durch die Folge $〈x_ν〉$ vollständig beschrieben, wenn das Abtasttheorem erfüllt ist:

$$T_{\rm A} \le \frac{1}{2 \cdot B_x}.$$

$B_x$ bezeichnet die absolute (einseitige) Bandbreite des Analogsignals $x(t)$. Diese sagt aus, dass die Spektralfunktion $X(f)$ für alle Frequenzen $| f | > B_x$ Null ist.

Abtastung eines Audiosignals

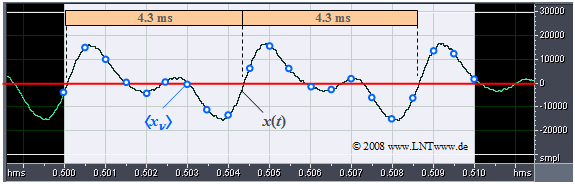
$\text{Beispiel 4:}$ Das Bild zeigt einen Ausschnitt eines Audiosignals der Dauer $10$ Millisekunden.

Obwohl das gesamte Signal ein breites Spektrum mit der Mittenfrequenz bei etwa $500 \hspace{0.05cm} \rm Hz$ besitzt, ist im betrachteten (kurzen) Zeitintervall ein (nahezu) periodisches Signal mit etwa der Periodendauer $T_0 = 4.3 \hspace{0.05cm} \rm ms$ zu erkennen. Daraus ergibt sich die Grundfrequenz zu

$$f_0 = 1/T_0 \approx 230 \hspace{0.05cm} \rm Hz.$$

Blau eingezeichnet sind die Abtastwerte im Abstand $T_{\rm A} = 0.5 \hspace{0.05cm} \rm ms$.

Diese Folge $〈x_ν〉$ von Abtastwerten würde allerdings nur dann die gesamte Information über das Analogsignal $x(t)$ beinhalten, wenn dieses auf den Frequenzbereich bis $1 \hspace{0.05cm} \rm kHz$ begrenzt wäre.
Sind im Signal $x(t)$ höhere Frequenzanteile enthalten, so muss $T_{\rm A}$ entsprechend kleiner gewählt werden.

$\text{Fazit:}$

Wenn die Signalwerte nur zu diskreten Zeitpunkten $($bei Vielfachen von $T_{\rm A})$ vorliegen, kann man auch die Autokorrelationsfunktion nur zu ganzzahligen Vielfachen von $T_{\rm A}$ bestimmen.
Mit den zeitdiskreten Signalwerten $x_ν = x(ν · T_{\rm A})$ und $x_{ν+k} = x((ν+k) · T_{\rm A})$ sowie der zeitdiskreten AKF $φ_k = φ_x(k · T_{\rm A})$ lässt sich somit die AKF–Berechnung wie folgt dargestellen:

$$\varphi_k = \overline {x_\nu \cdot x_{\nu + k} }.$$

Die überstreichende Linie kennzeichnet wieder die Zeitmittelung.

Wir stellen uns nun die Aufgabe, die AKF-Stützstellen $φ_0, \hspace{0.1cm}\text{...}\hspace{0.1cm} , φ_l$ aus $N$ Abtastwerten $(x_1, \hspace{0.1cm}\text{...}\hspace{0.1cm} , x_N)$ zu ermitteln, wobei der Parameter $l \ll N$ vorausgesetzt wird. Beispielsweise gelte $l = 100$ und $N = 100000$.

Die AKF-Berechnungsvorschrift lautet nun $($mit $0 ≤ k ≤ l)$:

$$\varphi_k = \frac{1}{N- k} \cdot \sum_{\nu = 1}^{N - k} x_{\nu} \cdot x_{\nu + k}.$$

Bringen wir den Faktor $(N - k)$ auf die linke Seite, so erhalten wir daraus $l + 1$ Gleichungen, nämlich:

$$k = 0\text{:} \hspace{0.4cm}N \cdot \varphi_0 \hspace{1.03cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{\rm 1} \hspace{0.35cm}+ x_{\rm 2} \cdot x_{\rm 2} \hspace{0.3cm}+\text{ ...} \hspace{0.25cm}+x_{\nu} \cdot x_{\nu}\hspace{0.35cm}+\text{ ...} \hspace{0.05cm}+x_{N} \cdot x_{N},$$

$$k= 1\text{:} \hspace{0.3cm}(N-1) \cdot \varphi_1 \hspace{0.08cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{\rm 2} \hspace{0.4cm}+ x_{\rm 2} \cdot x_{\rm 3} \hspace{0.3cm}+ \text{ ...} \hspace{0.18cm}+x_{\nu} \cdot x_{\nu + 1}\hspace{0.01cm}+\text{ ...}\hspace{0.08cm}+x_{N-1} \cdot x_{N},$$

$$\text{..................................................}$$

$$k \hspace{0.2cm}{\rm allg.\hspace{-0.1cm}:}\hspace{0.15cm}(N - k) \cdot \varphi_k \hspace{0.01cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{ {\rm 1} + k} \hspace{0.01cm}+ x_{\rm 2} \cdot x_{ {\rm 2}+ k}\hspace{0.1cm} + \text{ ...}\hspace{0.01cm}+x_{\nu} \cdot x_{\nu+k}\hspace{0.1cm}+\text{ ...}\hspace{0.01cm}+x_{N-k} \cdot x_{N},$$

$$\text{..................................................}$$

$$k = l\text{:} \hspace{0.3cm}(N - l) \cdot \varphi_l \hspace{0.14cm}=\hspace{0.1cm} x_{\rm 1} \cdot x_{ {\rm 1}+l} \hspace{0.09cm}+ x_{\rm 2} \cdot x_{ {\rm 2}+ l} \hspace{0.09cm}+ \text{ ...}\hspace{0.09cm}+x_{\nu} \cdot x_{\nu+ l} \hspace{0.09cm}+ \text{ ...}\hspace{0.09cm}+x_{N- l} \cdot x_{N}.$$

$\text{Fazit:}$ Nach diesem Schema ergibt sich der folgende Algorithmus:

Man definiert das Feld $\rm AKF\big[\hspace{0.05cm}0 : {\it l}\hspace{0.1cm}\big]$ vom Typ "float" und belegt alle Elemente mit Nullen vor.
Bei jedem Schleifendurchlauf $($indiziert mit der Variablen $k)$ werden die $l + 1$ Feldelemente ${\rm AKF}\big[\hspace{0.03cm}k\hspace{0.03cm}\big]$ jeweils um den Beitrag $x_ν · x_{ν+k}$ erhöht.
Alle $l+1$ Feldelemente werden allerdings nur dann bearbeitet, so lange die Laufvariable $k$ nicht größer als $N - l$ ist.
Es ist stets zu berücksichtigen, dass $ν + k ≤ N$ gelten muss. Das bedeutet, dass die Mittelung in den unterschiedlichen Feldern $\rm AKF\big[\hspace{0.03cm}0\hspace{0.03cm}\big]$ ... ${\rm AKF}\big[\hspace{0.03cm}l\hspace{0.03cm}\big]$ über eine unterschiedliche Anzahl von Summanden erfolgen muss.
Werden am Ende der Berechnung noch die in ${\rm AKF}\big[\hspace{0.03cm}k\hspace{0.03cm}\big]$ gespeicherten Werte durch die Anzahl der Summanden $(N - k)$ dividiert, so enthält dieses Feld die gesuchten diskreten AKF-Werte:

$$\varphi_x(k \cdot T_A)= {\rm AKF} \big[\hspace{0.03cm}k\hspace{0.03cm}\big].$$

Anmerkung: Bei $l \ll N$ kann man den Algorithmus vereinfachen, indem die Anzahl der Summanden für alle $k$–Werte gleich gewählt werden:

$$\varphi_k = \frac{1}{N- l} \cdot \sum_{\nu = 1}^{N - l} x_{\nu} \cdot x_{\nu + k}.$$

Genauigkeit der numerischen AKF-Berechnung

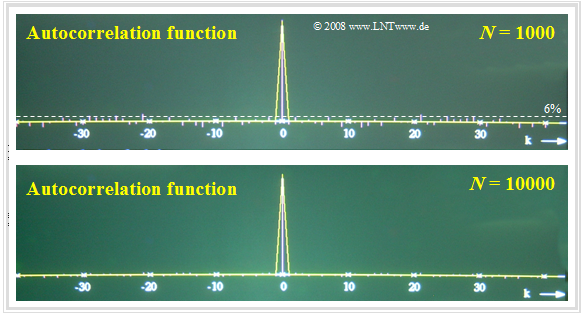
$\text{Beispiel 5:}$ Der entscheidende Parameter für die Qualität der numerischen AKF–Berechnung ist die Anzahl $N$ der berücksichtigten Abtastwerte.

In der oberen Grafik sehen Sie das Ergebnis der numerischen AKF-Berechnung für $N = 1000$.
Die untere Grafik gilt für $N = 10000$ Abtastwerte.

AKF bei statistisch unabhängigen Abtastwerten

Die betrachteten Zufallsgrößen sind hier voneinander statistisch unabhängig. Somit sollten eigentlich alle AKF–Werte mit Ausnahme des Wertes bei $k = 0$ identisch Null sein.

Bei $N = 10000$ (untere Grafik) beträgt der maximale Fehler nur noch etwa $1\%$ und ist bei dieser Darstellung fast nicht mehr sichtbar.

Dagegen wächst der Fehler bei $N = 1000$ (obere Grafik) bis auf $±6\%$ an.

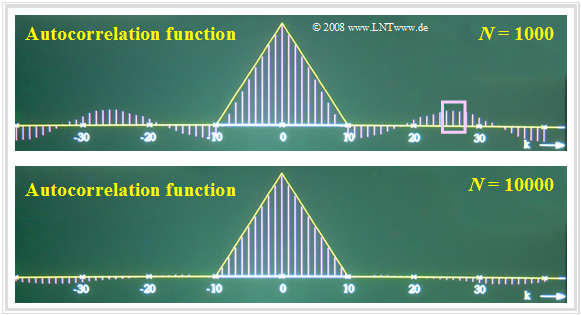
AKF bei korrelierten Abtastwerten

$\text{Beispiel 6:}$ Die Ergebnisse ändern sich, wenn eine Zufallsgröße mit inneren statistischen Bindungen vorliegt.

Betrachten wir beispielsweise eine dreieckförmige AKF mit $φ_x(k) ≠ 0$ für $\vert k \vert ≤ 10$, so erkennt man deutlich größere Abweichungen, nämlich

Fehler bis zu etwa $±15\%$ bei $N = 1000$,
Fehler bis zu etwa $±5\%$ bei $N = 10000$.

Begründung des schlechteren Ergebnisses gemäß $\text{Beispiel 6}$:

Aufgrund der inneren statistischen Bindungen liefern nun nicht mehr alle Abtastwerte die volle Information über den zugrundeliegenden Zufallsprozess.
Außerdem lassen die Bilder erkennen, dass bei der numerischen AKF–Berechnung einer Zufallsgröße mit statistischen Bindungen auch die Fehler korreliert sind.
Ist – wie beispielsweise im oberen Bild zu sehen – der AKF-Wert $φ_x({\rm 26})$ fälschlicherweise positiv und groß, so ergeben sich auch die benachbarten AKF-Werte $φ_x({\rm 25})$ und $φ_x({\rm 27})$ als positiv und mit ähnlichen Zahlenwerten. Dieser Bereich ist in der oberen Grafik durch das Rechteck markiert.