Contents
Wiener-Khintchine Theorem
In the remainder of this paper we restrict ourselves to ergodic processes. As was shown in last chapter the following statements then hold:
- Each individual sample function $x_i(t)$ is representative of the entire random process $\{x_i(t)\}$.
- All time means are thus identical to the corresponding coulter means.
- The autocorrelation function, which is generally affected by the two time parameters $t_1$ and $t_2$ now depends only on the time difference $τ = t_2 - t_1$ :
- $$\varphi_x(t_1,t_2)={\rm E}\big[x(t_{\rm 1})\cdot x(t_{\rm 2})\big] = \varphi_x(\tau)= \int^{+\infty}_{-\infty}x(t)\cdot x(t+\tau)\,{\rm d}t.$$
The autocorrelation function provides quantitative information about the (linear) statistical bindings within the ergodic process $\{x_i(t)\}$ in the time domain. The equivalent descriptor in the frequency domain is the power spectral density , often referred to as the power density spectrum.
$\text{Definition:}$ The power spectral density (PSD) of an ergodic random process $\{x_i(t)\}$ is the Fourier transform of the auto-correlation function (ACF):
- $${\it \Phi}_x(f)=\int^{+\infty}_{-\infty}\varphi_x(\tau) \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} \tau. $$
This functional is called the theorem of Wiener and Khinchin.
Similarly, the ACF can be computed as the inverse Fourier transform of the PSD (see page inverse Fourier transform in the book "Signal Representation"):
- $$ \varphi_x(\tau)=\int^{+\infty}_{-\infty} {\it \Phi}_x \cdot {\rm e}^{- {\rm j\hspace{0.05cm}\cdot \hspace{0.05cm} \pi}\hspace{0.05cm}\cdot \hspace{0.05cm} f \hspace{0.05cm}\cdot \hspace{0.05cm}\tau} {\rm d} f.$$
- The two equations are directly applicable only if the random process contains neither a DC component nor periodic components.
- Otherwise, one must proceed according to the specifications given in page Power spectral density with DC component .
Physical interpretation and measurement
The following figure shows an arrangement for (approximate) metrological determination of the power density spectrum ${\it \Phi}_x(f)$.
The following should be noted in this regard:
- The random signal $x(t)$ is applied to a (preferably) rectangular and (preferably) narrowband filter with center frequency $f$ and bandwidth $Δf$ where $Δf$ must be chosen sufficiently small according to the desired frequency resolution.
- The corresponding output signal $x_f(t)$ is squared and then the mean value is formed over a sufficiently long measurement period $T_{\rm M}$ . This gives the power of $x_f(t)$ or the power components of $x(t)$ in the spectral range from $f - Δf/2$ to $f + Δf/2$:
- $$P_{x_f} =\overline{x_f(t)^2}=\frac{1}{T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm}\rm d \it t.$$
- Division by $Δf$ leads from spectral power to power spectral density:
- $${{\it \Phi}_{x \rm +}}(f) =\frac{P_{x_f}}{{\rm \Delta} f} \hspace {0.5cm} {\rm bzw.} \hspace {0.5cm} {\it \Phi}_{x}(f) = \frac{P_{x_f}}{{\rm 2 \cdot \Delta} f}.$$
- Here denotes ${\it \Phi}_{x+}(f) = 2 - {\it \Phi}_x(f)$ the one-sided PSD defined only for positive frequencies. For negative frequencies, ${\it \Phi}_{x+}(f) = 0$. In contrast, for the commonly used two-sided PSD : ${\it \Phi}_x(-f) = {\it \Phi}_x(f)$.
- While the power $P_{x_f}$ tends to zero as the bandwidth $Δf$ becomes smaller, the power spectral density remains nearly constant above a sufficiently small value of $Δf$ For the exact determination of ${\it \Phi}_x(f)$ two boundary crossings are necessary:
- $${{\it \Phi}_x(f)} = \lim_{{\rm \Delta}f\to 0} \hspace{0.2cm} \lim_{T_{\rm M}\to\infty}\hspace{0.2cm} \frac{1}{{\rm 2 \cdot \Delta}f\cdot T_{\rm M}}\cdot\int^{T_{\rm M}}_{0}x_f^2(t) \hspace{0.1cm} \rm d \it t.$$
$\text{Conclusion:}$
- From this physical interpretation it further follows that the power spectral density is always real and can never become negative.
- The total signal power of $x(t)$ is then obtained by integration over all spectral components:
- $$P_x = \int^{\infty}_{0}{\it \Phi}_{x \rm +}(f) \hspace{0.1cm}{\rm d} f = \int^{+\infty}_{-\infty}{\it \Phi}_x(f)\hspace{0.1cm} {\rm d} f .$$
Reciprocity law of ACF duration and PSD bandwidth
All the Laws of Fourier Transform derived in the book "Signal Representation" for deterministic signals can also be applied to the auto-correlation function (ACF) and the Power Spectral Density (PSD) of a random process.
Due to the specific properties
- of autocorrelation function (always real and even).
- and power density spectrum (always real, even, and non–negative)
however, do not all laws yield meaningful results.
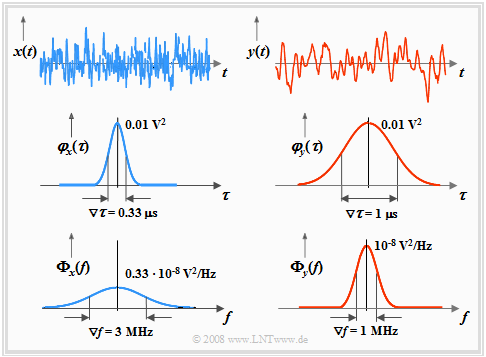
We now consider, as in the section Interpretation of the Autocorrelation Function two different ergodic random processes $\{x_i(t)\}$ and $\{y_i(t)\}$ based on
- of the two pattern signals $x(t)$ and $y(t)$ ⇒ upper sketch,
- of the two autocorrelation functions $φ_x(τ)$ and $φ_y(τ)$ ⇒ middle sketch,
- of the two power spectral densities ${\it \Phi}_x(f)$ and ${\it \Phi}_y(f)$ ⇒ bottom sketch.
Based on these graphs, the following statements can be made:
- The areas under the PSD curves are equal ⇒ the processes $\{x_i(t)\}$ and $\{y_i(t)\}$ have equal power:
- $${\varphi_x({\rm 0})}\hspace{0.05cm} =\hspace{0.05cm} \int^{+\infty}_{-\infty}{{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f \hspace{0.2cm} = \hspace{0.2cm}{\varphi_y({\rm 0})} = \int^{+\infty}_{-\infty}{\it \Phi}_y(f)} \hspace{0.1cm} {\rm d} f .$$
- The well known from classical (deterministic) system theory Reciprocity Theorem of time duration and bandwidth also applies here:
A narrow autocorrelation function corresponds to a broad power density spectrum and vice versa. - As a descriptive quantity, we use here the equivalent PSD bandwidth $∇f$ $($man speaks "Nabla-f"$)$, similarly defined as the equivalent ACF duration $∇τ$ im Kapitel Interpretation of the auto-correlation function:
- $${{\rm \nabla} f_x} = \frac {1}{{\it \Phi}_x(f = {\rm 0})} \cdot \int^{+\infty}_{-\infty}{\it \Phi}_x(f)} \hspace{0.1cm} {\rm d} f, \hspace{0.5cm}{ {\rm \nabla} \tau_x} = \frac {\rm 1}{ \varphi_x(\tau = \rm 0)} \cdot \int^{+\infty}_{-\infty}{\varphi_x(\tau )} \hspace{0.1cm} {\rm d} \tau.$$
- With these definitions, the following basic relationship holds:
- $${{\rm \nabla} \tau_x} \cdot {{\rm \nabla} f_x} = 1\hspace{1cm}{\rm resp.}\hspace{1cm} {{\rm \nabla} \tau_y} \cdot {{\rm \nabla} f_y} = 1.$$
$\text{Example 1:}$ We start from the graph at the top of this page:
- The characteristics of the higher frequency signal $x(t)$ are $∇τ_x = 0.33\hspace{0.08cm} \rm µs$ and $∇f_x = 3 \hspace{0.08cm} \rm MHz$.
- The equivalent ACF duration of the signal $y(t)$ is three times: $∇τ_y = 1 \hspace{0.08cm} \rm µs$.
- The equivalent PSD bandwidth is thus only more $∇f_y = ∇f_x/3 = 1 \hspace{0.08cm} \rm MHz$.
$\text{General:}$ The product of equivalent ACF duration ${ {\rm \nabla} \tau_x}$ and equivalent PSD bandwidth $ { {\rm \nabla} f_x}$ is always equal $1$:
- $${ {\rm \nabla} \tau_x} \cdot { {\rm \nabla} f_x} = 1.$$
$\text{Beispiel 2:}$ A limiting case of the reciprocity law represents the so-called white noise' :
- This includes all spectral components (up to infinity).
- The equivalent PSD bandwidth $∇f$ is infinite.
The law given here states that thus for the equivalent ACF duration $∇τ = 0$ must hold ⇒ the white noise has a dirac-shaped ACF.
For more on this topic, see the three-part tutorial video The AWGN channel, especially the second part
.
Leistungsdichtespektrum mit Gleichsignalkomponente
Wir gehen von einem gleichsignalfreien Zufallsprozess $\{x_i(t)\}$ aus. Weiter setzen wir voraus, dass der Prozess auch keine periodischen Anteile beinhaltet. Dann gilt:
- Die Autokorrelationsfunktion $φ_x(τ)$ verschwindet für $τ → ∞$.
- Das Leistungsdichtespektrum ${\it \Phi}_x(f)$ – berechenbar als die Fouriertransformierte von $φ_x(τ)$ – ist sowohl wert– als auch zeitkontinuierlich, also ohne diskrete Anteile.
Wir betrachten nun einen zweiten Zufallsprozess $\{y_i(t)\}$, der sich vom Prozess $\{x_i(t)\}$ lediglich durch eine zusätzliche Gleichsignalkomponente $m_y$ unterscheidet:
- $$\left\{ y_i (t) \right\} = \left\{ x_i (t) + m_y \right\}.$$
Die statistischen Beschreibungsgrößen des mittelwertbehafteten Zufallsprozesses $\{y_i(t)\}$ weisen dann folgende Eigenschaften auf:
- Der Grenzwert der AKF für $τ → ∞$ ist nun nicht mehr Null, sondern $m_y^2$. Im gesamten $τ$–Bereich von $–∞$ bis $+∞$ ist die AKF $φ_y(τ)$ um $m_y^2$ größer als $φ_x(τ)$:
- $${\varphi_y ( \tau)} = {\varphi_x ( \tau)} + m_y^2 . $$
- Nach den elementaren Gesetzen der Fouriertransformation führt der konstante AKF-Beitrag im PSD zu einer Diracfunktion $δ(f)$ mit dem Gewicht $m_y^2$:
- $${{\it \Phi}_y ( f)} = {\Phi_x ( f)} + m_y^2 \cdot \delta (f). $$
Nähere Informationen zur Diracfunktion finden Sie im Kapitel Gleichsignal - Grenzfall eines periodischen Signals des Buches „Signaldarstellung”. Weiterhin möchten wir Sie hier auf das Lernvideo Herleitung und Visualisierung der Diracfunktion hinweisen.
Numerische LDS-Ermittlung
Autokorrelationsfunktion und Leistungsdichtespektrum sind über die Fouriertransformation streng miteinander verknüpft. Dieser Zusammenhang gilt auch bei zeitdiskreter AKF-Darstellung mit dem Abtastoperator ${\rm A} \{ \varphi_x ( \tau ) \} $, also für
- $${\rm A} \{ \varphi_x ( \tau ) \} = \varphi_x ( \tau ) \cdot \sum_{k= - \infty}^{\infty} T_{\rm A} \cdot \delta ( \tau - k \cdot T_{\rm A}).$$
Der Übergang vom Zeit– in den Spektralbereich kann mit folgenden Schritten hergeleitet werden:
- Der Abstand $T_{\rm A}$ zweier Abtastwerte ist durch die absolute Bandbreite $B_x$ (maximal auftretende Frequenz innerhalb des Prozesses) über das Abtasttheorem festgelegt:
- $$T_{\rm A}\le\frac{1}{2B_x}.$$
- Die Fouriertransformierte der zeitdiskreten (abgetasteten) AKF ergibt ein mit ${\rm 1}/T_{\rm A}$ periodisches LDS:
- $${\rm A} \{ \varphi_x ( \tau ) \} \hspace{0.3cm} \circ\!\!-\!\!\!-\!\!\!-\!\!\bullet\, \hspace{0.3cm} {\rm P} \{{{\it \Phi}_x} ( f) \} = \sum_{\mu = - \infty}^{\infty} {{\it \Phi}_x} ( f - \frac {\mu}{T_{\rm A}}).$$
$\text{Fazit:}$ Da sowohl $φ_x(τ)$ als auch ${\it \Phi}_x(f)$ gerade und reelle Funktionen sind, gilt der Zusammenhang:
- $${\rm P} \{ { {\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{\infty} \varphi_x ( k T_{\rm A}) \cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
- Das Leistungsdichtespektrum (LDS) des zeitkontinuierlichen Prozesses erhält man aus ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ durch Bandbegrenzung auf den Bereich $\vert f \vert ≤ 1/(2T_{\rm A})$.
- Im Zeitbereich bedeutet diese Operation eine Interpolation der einzelnen AKF-Abtastwerte mit der ${\rm si}$–Funktion, wobei ${\rm si}(x)$ für $\sin(x)/x$ steht.
$\text{Beispiel 3:}$ Eine gaußförmige AKF $φ_x(τ)$ wird im Abstand $T_{\rm A}$ abgetastet, wobei das Abtasttheorem erfüllt ist:
- Die Fouriertransformierte der zeitdiskreten AKF ${\rm A} \{φ_x(τ) \}$ sei ${\rm P} \{ { {\it \Phi}_x} ( f) \}$.
- Diese mit ${\rm 1}/T_{\rm A}$ periodische Funktion ${\rm P} \{ { {\it \Phi}_x} ( f) \}$ ist dementsprechend unendlich weit ausgedehnt ( roter Kurvenzug ).
- Das LDS ${\it \Phi}_x(f)$ des zeitkontinuierlichen Prozesses $\{x_i(t)\}$ erhält man durch Bandbegrenzung auf den im Bild blau hinterlegten Frequenzbereich $\vert f · T_{\rm A} \vert ≤ 0.5$.
Genauigkeit der numerischen LDS-Berechnung
Für die nachfolgende Analyse gehen wir von folgenden Annahmen aus:
- Die zeitdiskrete AKF $φ_x(k · T_{\rm A})$ wurde aus $N$ Abtastwerten numerisch ermittelt. Wie bereits auf der Seite Genauigkeit der numerischen AKF-Berechnung gezeigt wurde, sind diese Werte fehlerhaft und die Fehler korreliert, wenn $N$ zu klein gewählt wurde.
- Zur Berechnung des periodischen Leistungsdichtespektrums (LDS) verwenden wir nur die AKF-Werte $φ_x(0)$, ... , $φ_x(K · T_{\rm A})$:
- $${\rm P} \{{{\it \Phi}_x} ( f) \} = T_{\rm A} \cdot \varphi_x ( k = 0) +2 T_{\rm A} \cdot \sum_{k = 1}^{K} \varphi_x ( k T_{\rm A})\cdot {\rm cos}(2{\rm \pi} f k T_{\rm A}).$$
$\text{Fazit:}$ Die Genauigkeit der LDS-Berechnung wird im starken Maße durch den Parameter $K$ bestimmt:
- Ist $K$ zu klein gewählt, so werden die eigentlich vorhandenen AKF-Werte $φ_x(k · T_{\rm A})$ mit $k > K$ nicht berücksichtigt.
- Bei zu großem $K$ werden auch solche AKF-Werte berücksichtigt, die eigentlich Null sein sollten und nur wegen der numerischen AKF-Berechnung endlich sind.
- Diese Werte sind allerdings – bedingt durch ein zu kleines $N$ bei der AKF–Ermittlung – nur Fehler, und beinträchtigen die LDS-Berechnung mehr als dass sie einen brauchbaren Beitrag zum Ergebnis liefern.
$\text{Beispiel 4:}$ Wir betrachten hier einen mittelwertfreien Prozess mit statistisch unabhängigen Abtastwerten.
- Deshalb sollte nur der AKF–Wert $φ_x(0) = σ_x^2$ von Null verschieden ist.
- Ermittelt man aber die AKF numerisch aus lediglich $N = 1000$ Abtastwerten, so erhält man auch für $k ≠ 0$ endliche AKF–Werte.
- Das obere Bild zeigt, dass diese fehlerhaften AKF–Werte bis zu $6\%$ des Maximalwertes betragen können.
- Unten ist das numerisch ermittelte Leistungsdichtespektrum dargestellt. Gelb ist der theoretische Verlauf dargestellt, der für $\vert f · T_{\rm A} \vert ≤ 0.5$ konstant sein sollte.
- Die grüne und die violette Kurve verdeutlichen, wie durch $K = 3$ bzw. $K = 10$ das Ergebnis gegenüber $K = 0$ verfälscht wird.
In diesem Fall (statistisch unabhängige Zufallsgrößen) wächst der Fehler monoton mit steigendem $K$. Bei einer Zufallsgröße mit statistischen Bindungen gibt es dagegen jeweils einen optimalen Wert für $K$.
- Wird dieser zu klein gewählt, so werden signifikante Bindungen nicht berücksichtigt.
- Ein zu großer Wert führt dagegen zu Oszillationen, die nur auf fehlerhafte AKF–Werte zurückzuführen sind.
Aufgaben zum Kapitel
Aufgabe 4.12: LDS eines Binärsignals
Aufgabe 4.12Z: Weißes Rauschen