Exercise 4.12: Power-Spectral Density of a Binary Signal

Binary square-wave signals

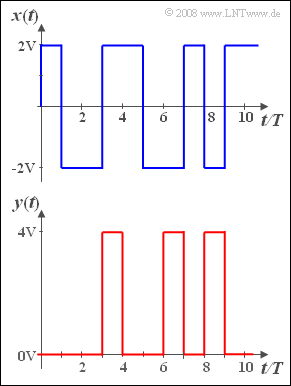
We consider a rectangular binary signal $x(t)$ with equal probability amplitude values $+2\hspace{0.05cm}\rm V$ and $-2\hspace{0.05cm}\rm V$.

The symbol duration is $T = 1 \hspace{0.05cm}\rm µ s$.
In Exercise 4.10 it has already been shown that the associated ACF is restricted to the range of $-T \le \tau\le +T$ and is triangular in this range:

$$\varphi_x (\tau) = 4 \hspace{0.05cm}{\rm V}^2 \cdot (1 - | \tau |/{T}).$$

It is assumed here that the individual symbols are statistically independent of each other.

The signal $y(t)$ sketched below is also binary and rectangular with the same symbol duration $T = 1 \hspace{0.05cm}\rm µ s$.

But the possible amplitude values are now $0\hspace{0.05cm}\rm V$ and $4\hspace{0.05cm}\rm V$.
The amplitude value $4\hspace{0.05cm}\rm V$ occurs less frequently than $0\hspace{0.05cm}\rm V$. It holds:

$${\rm Pr}(x(t) = 4 \hspace{0.05cm} {\rm V}) = p\hspace{0.5cm} {\rm with}\hspace{0.5cm} 0 < p \le 0.25.$$

Hints:

This exercise belongs to the chapter Power-Spectral Density.

Note the following Fourier correspondence, where ${\rm \Delta} (t)$ a triangular pulse symmetric about $t= 0$ with ${\rm \Delta} (t= 0) = 1$ and ${\rm \Delta} (t) = 0$ for $|t| \ge T$ denotes:

$${\rm \Delta} (t) \hspace{0.3cm} \circ\!\!\!\!\!\!\!\!\bullet\, \hspace{0.3cm} T \cdot {\rm si}^2 ( \pi f T).$$

Further, the notation ${\rm si}(x) = \sin(x)/x$ holds with the following integral value:

$$\int^1_0 {\rm si}^2 ( \pi \cdot u) \, {\rm d}u \ \approx 0.456.$$

Questions

${\it \Phi}_x(f = 0) \ = \ $

$\ \cdot 10^{-6} \ \rm V^2 /Hz$

${\it \Phi}_x(f = 500 \hspace{0.08cm}\rm kHz) \ = \ $

$\ \cdot 10^{-6} \ \rm V^2 /Hz$

${\it \Phi}_x(f = 1 \hspace{0.08cm}\rm MHz) \ = \ $

$\ \cdot 10^{-6} \ \rm V^2 /Hz$

$\varphi_y(\tau = 0) \ = \ $

$\ \rm V^2$

$\varphi_y(\tau = T) \ = \ $

$\ \rm V^2$

$\varphi_y(\tau = 2T) \ = \ $

$\ \rm V^2$

${\it \Phi}_x(f = 500 \hspace{0.08cm}\rm kHz) \ = \ $

$\ \cdot 10^{-6} \ \rm V^2 /Hz$

$P_{\rm M} \ = \ $

$\ \rm V^2$

Musterlösung

Solution

Power-spectral density with DC component

(1) The PSD is the Fourier transform of the ACF.

With the Fourier correspondence on the data side and $x_0 = 2\hspace{0.05cm}\rm V$ one obtains:

$${\it \Phi}_x(f)= x_{\rm 0}^2 \cdot T \cdot {\rm si}^2(\pi f T).$$

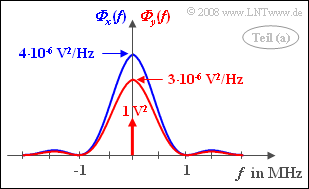
The PSD values we are looking for are:

$${\it \Phi}_x(f = 0)\hspace{0.15cm}\underline {=4} \cdot 10^{-6} \rm V^2 /Hz,$$

$${\it \Phi}_x(f = 500 \hspace{0.05cm}\rm kHz)\hspace{0.15cm}\underline {=1.62} \cdot 10^{-6} \rm V^2 /Hz,$$

$${\it \Phi}_x(f = 1 \hspace{0.05cm}\rm MHz)\hspace{0.15cm}\underline {=0}.$$

At $f = 1 \hspace{0.05cm}\rm MHz $ the power-spectral density has the first zero.

Auto-correlation function with DC component

(2) Due to the rectangular waveform, the triangular shape of the ACF does not change in principle.

The ACF value at $\tau = 0$ again gives the second order moment.
With $p = 0.25$ one obtains:

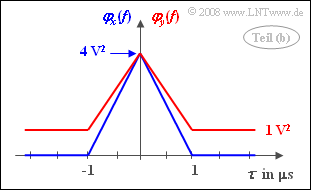
$$\varphi_y( 0) = {1}/{4}\cdot {(\rm 4\hspace{0.05cm}V)}^2 + {3}/{4}\cdot {(\rm 0\hspace{0.05cm}V)}^2 \hspace{0.15cm}\underline{= {\rm 4\,V^2}}.$$

From $\tau =T$ the ACF is constantly equal to $m_y^2$.
With probability $p = 0.25$ and $m_y = p \cdot {\rm 4\hspace{0.05cm}V} + (1-p)\cdot {\rm 0\hspace{0. 05cm}V} = 1 \, \rm V$ obtains from $\tau =T$ the constant value $\varphi_y( \tau >T) \hspace{0.15cm}\underline {=\rm 1\,V^2}$.

(3) The ACF can also be represented as follows:

$$\varphi_y(\tau) = 1\hspace{0.05cm}{\rm V}^2 + 3\hspace{0.05cm}{\rm V}^2 \cdot \Delta (\tau).$$

The ACF DC component $($with $1\hspace{0.05cm}{\rm V}^2)$ leads to a Dirac function in the PSD at $f = 0$ ⇒ see sketch for subtask (1).
The triangularförm ACF term causes a continuous PSD component corresponding to the $\rm si^2$-form:

$${\it \Phi}_y(f)= 1{\rm V}^2 \cdot {\rm \delta } (f) + 3 \cdot 10^{-6}\ {\rm V^2\hspace{-0.1cm}/Hz} \cdot {\rm si}^2(\pi f T).$$

For $f = 500 \hspace{0.05cm}\rm kHz$ ⇒ $f \cdot T =0.5$ the PSD value results to ${\underline {1.216} \cdot 10^{-6} \rm V^2 /Hz}$.

(4) The power can be calculated as an integral over the PSD.

Taking into account the spectral limitation to $ 1 \hspace{0.05cm}\rm MHz$ one obtains with the substitution $u =f \cdot T$:

$$P_{\rm M} = 1{\rm V}^2 + 3 \cdot 10^{-6} {{\rm V^2} /{\rm Hz}} \cdot \int^{\rm 1 MHz}_{-\rm 1 MHz} {\rm si}^2(\pi f T)\hspace{0.1cm}{\rm d}f = 1{\rm V}^2 + 3 V^2 \cdot 2 \cdot \int^{1}_{\rm 0} {\rm si}^2(\pi u)\hspace{0.1cm}{\rm d}u = (1 + 3\cdot 2 \cdot 0.456)\,{\rm V^2} \hspace{0.15cm}\underline{= 3.736 \, {\rm V^2}}. $$

If, on the other hand, all spectral components were covered, the average power would result in $\varphi_y( \tau= 0) = 4 \, {\rm V^2}$.