Generalization to N-Dimensional Random Variables

Correlation matrix

So far, only statistical bindings between two (scalar) random variables have been considered For the more general case of a random variable with $N$ dimensions, a vector– or matrix representation is convenient.

For the following description it is assumed:

The $N$-dimensional random variable is represented as a vector:

$${\mathbf{x}} = \big[\hspace{0.03cm}x_1, \hspace{0.03cm}x_2, \hspace{0.1cm}\text{...} \hspace{0.1cm}, \hspace{0.03cm}x_N \big]^{\rm T}.$$

Here $\mathbf{x}$ is a column vector, which can be seen from the addition $\rm T$ - this stands for "transposed" - of the specified row vector.

Let $N$ components $x_i$ each be one-dimensional real Gaussian random variables.

$\text{definition:}$ Statistical bindings between the $N$ random variables are fully described by the correlation matrix :

$${\mathbf{R} } =\big[ R_{ij} \big] = \left[ \begin{array}{cccc}R_{11} & R_{12} & \cdots & R_{1N} \ R_{21} & R_{22}& \cdots & R_{2N} \ \cdots & \cdots & \cdots \ R_{N1} & R_{N2} & \cdots & R_{NN} \end{array} \right] .$$

The $N^2$ elements of this $N×N$ matrix each indicate the first-order joint moment between two components:

$$R_{ij}= { {\rm E}\big[x_i \cdot x_j \big] } = R_{ji} .$$

Thus, in vector notation, the correlation matrix is:

$$\mathbf{R}= {\rm E\big[\mathbf{x} \cdot {\mathbf{x} }^{\rm T} \big] } .$$

Please note:

$\mathbf{x}$ is a column vector with $N$ dimensions and the transposed vector $\mathbf{x}^{\rm T}$ a row vector of equal length ⇒ the product $\mathbf{x} ⋅ \mathbf{x}^{\rm T}$ gives a $N×N$–matrix.
In contrast $\mathbf{x}^{\rm T}⋅ \mathbf{x}$ would be a $1×1$–matrix, i.e. a scalar.
For the special case of complex components $x_i$ not considered further here, the matrix elements are also complex:

$$R_{ij}= {{\rm E}\big[x_i \cdot x_j^{\star} \big]} = R_{ji}^{\star} .$$

The real parts of the correlation matrix ${\mathbf{R} }$ are still symmetric about the main diagonal, while the imaginary parts differ by sign.

Covariance matrix

$\text{Definition:}$ One moves from the correlation matrix $\mathbf{R} =\left[ R_{ij} \right]$ to the so-called covariance matrix

$${\mathbf{K} } =\big[ K_{ij} \big] = \left[ \begin{array}{cccc}K_{11} & K_{12} & \cdots & K_{1N} \ K_{21} & K_{22}& \cdots & K_{2N} \ \cdots & \cdots & \cdots \ K_{N1} & K_{N2} & \cdots & K_{NN} \end{array} \right] ,$$

if the matrix elements $K_{ij} = {\rm E}\big[(x_i - m_i) - (x_j - m_j)\big]$ each specify a first order central moment .

Thus, with the vector $\mathbf{m} = [m_1, m_2$, ... , $m_N]^{\rm T}$ can also be written:

$$\mathbf{K}= { {\rm E}\big[(\mathbf{x} - \mathbf{m}) (\mathbf{x} - \mathbf{m})^{\rm T} \big] } .$$

It should be explicitly noted that $m_1$ denotes the mean value of the component $x_1$ and $m_2$ denotes the mean value of $x_2$ - not, for example, the first or second order moment.

The covariance matrix $\mathbf{K}$ shows the following further properties for real mean-free Gaussian quantities:

The element of $i$-th row and $j$-th column is with the two scatterers $σ_i$ and $σ_j$ and the Correlation coefficient $ρ_{ij}$:

$$K_{ij} = σ_i ⋅ σ_j ⋅ ρ_{ij} = K_{ji}.$$

Adding the relation $ρ_{ii} = 1$, we obtain for the covariance matrix:

$${\mathbf{K}} =\left[ K_{ij} \right] = \left[ \begin{array}{cccc} \sigma_{1}^2 & \sigma_{1}\cdot \sigma_{2}\cdot\rho_{12} & \cdots & \sigma_{1}\cdot \sigma_{N} \cdot \rho_{1N} \\ \sigma_{2} \cdot \sigma_{1} \cdot \rho_{21} & \sigma_{2}^2& \cdots & \sigma_{2} \cdot \sigma_{N} \cdot\rho_{2N} \cdot \cdots & \cdots & \cdots \sigma_{N} \cdot \sigma_{1} \cdot \rho_{N1} & \sigma_{N}\cdot \sigma_{2} \cdot\rho_{N2} & \cdots & \sigma_{N}^2 \end{array} \right] .$$

Because of the relation $ρ_{ij} = ρ_{ji}$ the covariance matrix is always symmetric about the main diagonal for real quantities. For complex quantities, $ρ_{ij} = ρ_{ji}^{\star}$ would hold.

$\text{Example 1:}$ We consider the three covariance matrices:

$${\mathbf{K}_2} = \left[ \begin{array}{cc} 1 & -0.5 \\ -0.5 & 1 \end{array} \right], \hspace{0.9cm}{\mathbf{K}_3} = 4 \cdot \left[ \begin{array}{ccc} 1 & 1/2 & 1/4\\ 1/2 & 1 & 3/4 \\ 1/4 & 3/4 & 1 \end{array}\right], \hspace{0.9cm}{\mathbf{K}_4} = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 4 & 0 & 0 \\ 0 & 0 & 9 & 0 \\ 0 & 0 & 0 & 16 \end{array} \right].$$

$\mathbf{K}_2$ describes a 2D random variable, where the correlation coefficient $ρ$ between the two components is $-0.5$ and both components have dispersion $σ = 1$ .
For the 3D random variable according to $\mathbf{K}_3$ all components have the same scattering $σ = 2$ (please note prefactor). The strongest bindings here are between $x_2$ and $x_3$, where $ρ_{23} = 3/4$ holds.
The four components of the random variable denoted by $\mathbf{K}_4$ are uncorrelated, with Gaussian WDF also statistically independent. The variances are $σ_i^2 = i^2$ for $i = 1$, ... , $4$ ⇒ variances $σ_i = i$.

Relationship between covariance matrix and PDF

$\text{Definition:}$ The probability density function (PDF) of an $N$-dimensional Gaussian random variable $\mathbf{x}$ is:

$$f_\mathbf{x}(\mathbf{x})= \frac{1}{\sqrt{(2 \pi)^N \cdot \vert\mathbf{K}\vert } }\hspace{0.05cm}\cdot \hspace{0.05cm} {\rm e}^{-1/2\hspace{0.05cm}\cdot \hspace{0.05cm}(\mathbf{x} - \mathbf{m})^{\rm T}\hspace{0.05cm}\cdot \hspace{0.05cm}\mathbf{K}^{-1} \hspace{0.05cm}\cdot \hspace{0.05cm}(\mathbf{x} - \mathbf{m}) } .$$

Here denote:

$\mathbf{x}$ the column vector of the considered $N$–dimensional random variable,
$\mathbf{m}$ the column vector of the associated mean values,
$\mathbf{K}\vert$ the determinant of the $N×N$-covariance matrix $\mathbf{K}$ - a scalar quantity,
$\mathbf{K}^{-1}$ the inverse of $\mathbf{K}$; this is also an $N×N$-matrix.

The multiplications of the row vector $(\mathbf{x} - \mathbf{m})^{\rm T}$, the inverse matrix $\mathbf{K}^{-1}$ and the column vector $(\mathbf{x} - \mathbf{m})$ yields a scalar in the argument of the exponential function.

$\text{Example 2:}$ We consider as in $\text{Example 1}$ again a 4D random variable $\mathbf{x}$ whose covariance matrix is occupied only on the main diagonal:

$${\mathbf{K} } = \left[ \begin{array}{cccc} \sigma_{1}^2 & 0 & 0 & 0 \\ 0 & \sigma_{2}^2 & 0 & 0 \\ 0 & 0 & \sigma_{3}^2 & 0 \\ 0 & 0 & 0 & \sigma_{4}^2 \end{array} \right].$$

Their determinant is $\vert \mathbf{K}\vert = σ_1^2 - σ_2^2 - σ_3^2 - σ_4^2$. The inverse covariance matrix results to:

$${\mathbf{K} }^{-1} \cdot {\mathbf{K } } = \left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array} \right] \hspace{0.5cm}\rightarrow \hspace{0.5cm} {\mathbf{K} }^{-1} = \left[ \begin{array}{cccc} \sigma_{1}^{-2} & 0 & 0 & 0 \\ 0 & \sigma_{2}^{-2} & 0 & 0 \\ 0 & 0 & \sigma_{3}^{-2} & 0 \\ 0 & 0 & 0 & \sigma_{4}^{-2} \end{array} \right].$$

Thus, for zero mean quantities $(\mathbf{m = 0})$ the PDF is:

$$\mathbf{ f_{\rm x} }(\mathbf{x})= \frac{1}{ {(2 \pi)^2 \cdot \sigma_1\cdot \sigma_2\cdot \sigma_3\cdot \sigma_4} }\cdot {\rm e}^{-({x_1^2}/{2\sigma_1^2} \hspace{0.1cm}+\hspace{0.1cm}{x_2^2}/{2\sigma_2^2}\hspace{0.1cm}+\hspace{0.1cm}{x_3^2}/{2\sigma_3^2}\hspace{0.1cm}+\hspace{0.1cm}{x_4^2}/{2\sigma_4^2}) } .$$

A comparison with the chapter Probability density function and cumulative distribution function shows that it is a 4D random variable with statistically independent and uncorrelated components, since the following condition is satisfied:

$$\mathbf{f_x}(\mathbf{x})= \mathbf{f_{x1 } }(\mathbf{x_1}) \cdot \mathbf{f_{x2} }(\mathbf{x_2}) \cdot \mathbf{f_{x3} }(\mathbf{x_3} ) \cdot \mathbf{f_{x4} }(\mathbf{x_4} ) .$$

The case of correlated components is discussed in detail in the exercises on the chapter

.

The following links refer to two pages at the end of the chapter with basics of matrix opeations:

Eigenwerte und Eigenvektoren

Wir gehen weiter von einer $N×N$–Kovarianzmatrix $\mathbf{K}$ aus.

$\text{Definition:}$ Aus der $N×N$–Kovarianzmatrix $\mathbf{K}$ lassen sich die $N$ Eigenwerte $λ_1$, ... , $λ_N$ wie folgt berechnen:

$$\vert {\mathbf{K} } - \lambda \cdot {\mathbf{E} }\vert = 0.$$

$\mathbf{E}$ ist die Einheits-Diagonalmatrix der Dimension $N$.

$\text{Beispiel 3:}$ Ausgehend von einer 2×2-Matrix $\mathbf{K}$ mit $K_{11} = K_{22} = 1$ und $K_{12} = K_{21} = 0.8$ erhält man als Bestimmungsgleichung:

$${\rm det}\left[ \begin{array}{cc} 1- \lambda & 0.8 \\ 0.8 & 1- \lambda \end{array} \right] = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} (1- \lambda)^2 - 0.64 = 0.$$

Die beiden Eigenwerte sind somit $λ_1 = 1.8$ und $λ_2 = 0.2$.

$\text{Definition:}$ Mit den so ermittelten Eigenwerten $λ_i \ (i = 1$, ... , $N)$ kann man die dazugehörigen Eigenvektoren $\boldsymbol{\xi_i}$ berechnen.

Die $N$ vektoriellen Bestimmungsgleichungen lauten dabei:

$$({\mathbf{K} } - \lambda_i \cdot {\mathbf{E} }) \cdot {\boldsymbol{\xi_i} } = 0\hspace{0.5cm}(i= 1, \hspace{0.1cm}\text{...} \hspace{0.1cm} , N).$$

$\text{Beispiel 4:}$ In Fortsetzung der Rechnung im $\text{Beispiel 3}$ ergeben sich die beiden folgenden Eigenvektoren:

$$\left[ \begin{array}{cc} 1- 1.8 & 0.8 \\ 0.8 & 1- 1.8 \end{array} \right]\cdot{\boldsymbol{\xi_1} } = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\boldsymbol{\xi_1} } = {\rm const.} \cdot\left[ \begin{array}{c} +1 \\ +1 \end{array} \right],$$

$$\left[ \begin{array}{cc} 1- 0.2 & 0.8 \\ 0.8 & 1- 0.2 \end{array} \right]\cdot{\boldsymbol{\xi_2} } = 0 \hspace{0.5cm}\Rightarrow \hspace{0.5cm} {\boldsymbol{\xi_2} } = {\rm const.} \cdot\left[ \begin{array}{c} -1 \\ +1 \end{array} \right].$$

Bringt man die Eigenvektoren in die so genannte Orthonormalfom $($jeweils mit Betrag $1)$, so lauten sie:

$${\boldsymbol{\xi_1} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} +1 \\ +1 \end{array} \right], \hspace{0.5cm}{\boldsymbol{\xi_2} } = \frac{1}{\sqrt{2} } \cdot\left[ \begin{array}{c} -1 \\ +1 \end{array} \right].$$

Nutzung von Eigenwerten in der Informationstechnik

rechts

Abschließend soll diskutiert werden, wie Eigenwert und Eigenvektor in der Informationstechnik genutzt werden können, beispielsweise zum Zwecke der Datenreduktion.

Wir gehen von den gleichen Parameterwerten wie in $\text{Beispiel 3}$ und $\text{Beispiel 4}$ aus.

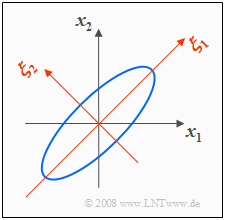
Mit $σ_1 = σ_2 = 1$ und $ρ = 0.8$ ergibt sich die rechts skizzierte 2D-WDF mit elliptischen Höhenlinien.
Die Ellipsenhauptachse liegt hier wegen $σ_1 = σ_2$ unter einem Winkel von $45^\circ$.

In der Grafik ist zusätzlich das $(ξ_1, ξ_2)$-Koordinatensystem eingezeichnet, das durch die Eigenvektoren $\mathbf{ξ}_1$ und $\mathbf{ξ}_2$ der Korrelationsmatrix aufgespannt wird:

Die Eigenwerte $λ_1 = 1.8$ und $λ_2 = 0.2$ geben die Varianzen bezüglich des neuen Koordinatensystems an.
Die Streuungen sind somit $σ_1 = \sqrt{1.8} ≈ 1.341$ und $σ_2 = \sqrt{0.2} ≈ 0.447$.

$\text{Beispiel 5:}$ Soll eine 2D-Zufallsgröße $\mathbf{x}$ in seinen beiden Dimensionen $x_1$ und $x_2$ im Bereich zwischen $–5σ$ und $+5σ$ im Abstand $Δx = 0.01$ quantisiert werden, so gibt es $\rm 10^6$ mögliche Quantisierungswerte $(σ_1 = σ_2 = σ = 1$ vorausgesetzt$)$.

Dagegen ist die Anzahl der möglichen Quantisierungswerte bei der gedrehten Zufallsgröße $\mathbf{ξ}$ um den Faktor $1.341 · 0.447 ≈ 0.6$ geringer.
Das bedeutet: Allein durch die Drehung des Koordinatensystems um $45^\circ$ ⇒ Transformation der 2D–Zufallsgröße wird die Datenmenge um ca. $40\%$ reduziert.

Die Ausrichtung entsprechend den Hauptdiagonalen wurde für den zweidimensionalen Fall bereits auf der Seite Drehung des Koordinatensystems behandelt, und zwar basierend auf geometrischen und trigonometrischen Überlegungen.

Die Problemlösung mit Eigenwert und Eigenvektor ist äußerst elegant und problemlos auf beliebig große Dimensionen $N$ erweiterbar.

Basics of matrix operations: Determinant of a matrix

Wir betrachten die beiden quadratischen Matrizen mit Dimension $N = 2$ bzw. $N = 3$:

$${\mathbf{A}} = \left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right], \hspace{0.5cm}{\mathbf{B}} = \left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\right].$$

Die Determinanten dieser beiden Matrizen lauten:

$$|{\mathbf{A}}| = a_{11} \cdot a_{22} - a_{12} \cdot a_{21},$$

$$|{\mathbf{B}}| = b_{11} \cdot b_{22} \cdot b_{33} + b_{12} \cdot b_{23} \cdot b_{31} + b_{13} \cdot b_{21} \cdot b_{32} - b_{11} \cdot b_{23} \cdot b_{32} - b_{12} \cdot b_{21} \cdot b_{33}- b_{13} \cdot b_{22} \cdot b_{31}.$$

$\text{Bitte beachten Sie:}$

Die Determinante von $\mathbf{A}$ entspricht geometrisch der Fläche des durch die Zeilenvektoren $(a_{11}, a_{12})$ und $(a_{21}, a_{22})$ aufgespannten Parallelogramms.
Die Fläche des durch die beiden Spaltenvektoren $(a_{11}, a_{21})^{\rm T}$ und $(a_{12}, a_{22})^{\rm T}$ festgelegten Parallelogramms ist ebenfalls $\vert \mathbf{A}\vert$.
Dagegen ist die Determinante der Matrix $\mathbf{B}$ bei analoger geometrischer Interpretation als Volumen zu verstehen.

Für $N > 2$ ist es möglich, sogenannte Unterdeterminanten zu bilden.

Die Unterdeterminante einer $N×N$–Matrix bezüglich der Stelle $(i, j)$ ist die Determinante der $(N–1)×(N–1)$–Matrix, die sich ergibt, wenn man die $i$-te Zeile und die $j$-te Spalte streicht.
Als Kofaktor bezeichnet man dann den Wert der Unterdeterminante gewichtet mit dem Vorzeichen $(–1)^{i+j}$.

$\text{Beispiel 6:}$ Ausgehend von der $3×3$–Matrix $\mathbf{B}$ lauten die Kofaktoren der zweiten Zeile:

$$B_{21} = -(b_{12} \cdot b_{23} - b_{13} \cdot b_{32})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j =3,$$

$$B_{22} = +(b_{11} \cdot b_{23} - b_{13} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=4,$$

$$B_{23} = -(b_{11} \cdot b_{32} - b_{12} \cdot b_{31})\hspace{0.3cm}{\rm da}\hspace{0.3cm} i+j=5.$$

Die Determinante von $\mathbf{B}$ ergibt sich mit diesen Kofaktoren zu:

$$\vert {\mathbf{B} } \vert = b_{21} \cdot B_{21} +b_{22} \cdot B_{22} +b_{23} \cdot B_{23}.$$

Die Determinante wurde hier nach der zweiten Zeile entwickelt.
Entwickelt man $\mathbf{B}$ nach einer anderen Zeile oder Spalte, so ergibt sich für $\vert \mathbf{B} \vert$ natürlich der gleiche Zahlenwert.

Basics of matrix operations: Inverse of a matrix

Häufig benötigt man die Inverse $\mathbf{M}^{–1}$ der quadratischen Matrix $\mathbf{M}$. Die inverse Matrix $\mathbf{M}^{–1}$ besitzt die gleiche Dimension $N$ wie $\mathbf{M}$ und ist wie folgt definiert, wobei $\mathbf{E}$ wieder die Einheitsmatrix (Diagonalmatrix) bezeichnet:

$${\mathbf{M}}^{-1} \cdot {\mathbf{M}} ={\mathbf{E}} = \left[ \begin{array}{cccc} 1 & 0 & \cdots & 0 \\ 0 & 1 & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots \\ 0 & 0 & \cdots & 1 \end{array} \right] .$$

$\text{Beispiel 7:}$ Die Inverse der $2×2$–Matrix $\mathbf{A}$ lautet demnach:

$$\left[ \begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array} \right]^{-1} = \frac{1}{\vert{\mathbf{A} }\vert} \hspace{0.1cm}\cdot \left[ \begin{array}{cc} a_{22} & -a_{12} \\ -a_{21} & a_{11} \end{array} \right].$$

Hierbei gibt $\vert\mathbf{A}\vert = a_{11} · a_{22} - a_{12} · a_{21}$ die Determinante an.

$\text{Beispiel 8:}$ Entsprechend gilt für die $3×3$–Matrix $\mathbf{B}$:

$$\left[ \begin{array}{ccc} b_{11} & b_{12} & b_{13}\\ b_{21} & b_{22} & b_{23}\\ b_{31} & b_{32} & b_{33} \end{array}\right]^{-1} = \frac{1}{\vert{\mathbf{B} }\vert} \hspace{0.1cm}\cdot\left[ \begin{array}{ccc} B_{11} & B_{21} & B_{31}\\ B_{12} & B_{22} & B_{32}\\ B_{13} & B_{23} & B_{33} \end{array}\right].$$

Die Determinante $\vert\mathbf{B}\vert$ einer $3×3$–Matrix wurde auf der letzten Seite angegeben, ebenso wie die Berechnungsvorschrift der Kofaktoren $B_{ij}$:
Diese beschreiben die Unterdeterminanten von $\mathbf{B}$, gewichtet mit den Positionsvorzeichen $(–1)^{i+j}$.
Zu beachten ist die Vertauschung der Zeilen und Spalten bei der Inversen.