Exercise 3.9: Circular Arc and Parabola

• Return to book

Locus curves in FM:
Arc and Parabola

We now consider the frequency modulation of a cosine source signal

$$q(t) = A_{\rm N} \cdot \cos(2 \pi \cdot f_{\rm N} \cdot t )$$

with amplitude  $A_{\rm N} = 1 \ \rm V$  and frequency $f_{\rm N} = 5 \ \rm kHz$.

• The modulation index (phase deviation) is  $η = 2.4$.
• The corresponding low-pass signal with normalized carrier amplitude  $(A_{\rm T} = 1)$ is:

$$s_{\rm TP}(t) = \sum_{n = - \infty}^{+\infty}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$

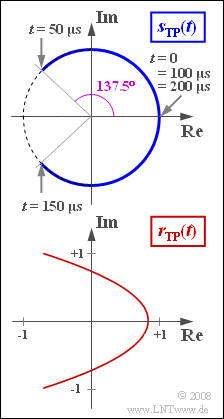
• This represents an arc.  Within the period $T_{\rm N} = 1/f_{\rm N} = 200 \ \rm µ s$  the following phase angles result:

$$\phi(0) = 0, \hspace{0.2cm}\phi(0.25 \cdot T_{\rm N}) = \eta, \hspace{0.2cm}\phi(0.5 \cdot T_{\rm N})= 0,\hspace{0.2cm} \phi(0.75 \cdot T_{\rm N})= -\eta,\hspace{0.2cm}\phi(T_{\rm N})= 0.$$

• Theoretically, the channel bandwidth required to transmit this signal is infinite.

However, if the bandwidth is limited to  $B_{\rm K} = 25 \ \rm kHz$, for example,the equivalent low-pass signal of the received signal can be described as follows:

$$r_{\rm TP}(t) = \sum_{n = - 2}^{+2}{\rm J}_n (\eta) \cdot {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm}n\hspace{0.05cm}\cdot \hspace{0.05cm}\omega_{\rm N} \hspace{0.05cm}\cdot \hspace{0.05cm} t}.$$

In this case, the result is a parabolic locus curve

$$y^2 + a \cdot x + b = 0,$$

which will be analyzed in this task.

Hints:

• This exercise belongs to the chapter  Frequency Modulation.
• Reference is also made to the chapter  Phase Modulation  and particularly to the section  Signal characteristics with frequency modulation.
• During calculation, assume the following values of the Bessel function:

$${\rm J}_0 (2.4) \approx 0, \hspace{0.2cm}{\rm J}_1 (2.4) = -{\rm J}_{-1} (2.4)\approx 0.52, \hspace{0.2cm}{\rm J}_2 (2.4) = {\rm J}_{-2} (2.4)\approx 0.43.$$

Question

1

What is the modulator constant  $K_{\rm FM}$?

$K_{\rm FM} \ = \ $ $\ \cdot 10^4 \ \rm (Vs)^{-1}$

2

Calculate the real part $x(t) = {\rm Re}\big[r_{\rm TP}(t)\big]$  of the equivalent low-pass signal and give its maximum and minimum.

$x_{\rm max} \ = \ $

$x_{\rm min} \ = \ $

3

What is the maximum and minimum of the imaginary part  $y(t) = {\rm Im}\big[r_{\rm TP}(t)\big]$?

$y_{\rm max} \ = \ $

$y_{\rm min} \ = \ $

4

What are the phase values for all multiples of  $T_{\rm N}/2$?

$ϕ(t = n · T_{\rm N}/2) \ = \ $ $\ \rm degrees$

5

What is the maximum phase angle  $ϕ_{\rm max}$?  Interpret the result.

$ϕ_{\rm max} \ = \ $ $\ \rm degrees$

6

Show that the locus curve can be given in the form  $y^2 + a · x + b = 0$ .  Determine the parabolic parameters  $a$  and  $b$.

$a\ = \ $

$b\ = \ $

Solution

Solution

(1)  Bei Frequenzmodulation eines Cosinussignals gilt für den Modulationsindex:

$$\eta = \frac{K_{\rm FM} \cdot A_{\rm N}}{ \omega_{\rm N}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm} K_{\rm FM} = \frac{2 \pi \cdot f_{\rm N }\cdot \eta}{ A_{\rm N}} = \frac{2 \pi \cdot 5 \cdot 10^3 \,{\rm Hz}\cdot 2.4}{ 1\,{\rm V}} \hspace{0.15cm}\underline {\approx 7.54 }\cdot 10^4 \,\,{\rm V}^{-1}{\rm s}^{-1}\hspace{0.05cm}.$$

(2)  Die angegebene Gleichung für das äquivalente TP–Signal lautet in ausgeschriebener Form mit  $γ = ω_{\rm N} · t$  unter Berücksichtigung von  ${\rm J}_{–1} = –{\rm J}_1$  und  ${\rm J}_{–2} = {\rm J}_2$:

$$r_{\rm TP}(t) = {\rm J}_0 + \left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} - {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} \gamma} \right]\cdot {\rm J}_1 \hspace{0.27cm} +\left[ {\rm e}^{\hspace{0.05cm}{\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} + {\rm e}^{\hspace{0.05cm}{-\rm j} \hspace{0.05cm}\cdot \hspace{0.05cm} 2\gamma} \right]\cdot {\rm J}_2 = {\rm J}_0 + 2 \cdot {\rm j} \cdot {\rm J}_1 \cdot \sin (\gamma)+ 2 \cdot {\rm J}_2 \cdot \cos (2\gamma)\hspace{0.05cm} .$$

• Somit ergibt sich für den Realteil allgemein bzw. für  $η = 2.4$, das heißt  ${\rm J}_0 = 0$  und  ${\rm J}_2 = 0.43$:

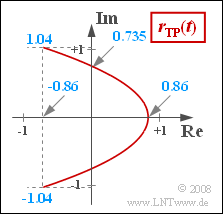
$$x(t) = {\rm J}_0 + 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) = 2 \cdot {\rm J}_2 \cdot \cos (2 \omega_{\rm N} t ) \hspace{0.3cm} \Rightarrow \hspace{0.3cm} x_{\rm max} = 2 \cdot {\rm J}_2\hspace{0.15cm}\underline { = 0.86}, \hspace{0.3cm} x_{\rm min} = -x_{\rm max} \hspace{0.15cm}\underline {= -0.86}\hspace{0.05cm}.$$

(3)  Entsprechend dem Ergebnis der Teilaufgabe  (2)  erhält man für den Imaginärteil  $({\rm J}_1 = 0.52)$:

$$y(t) = 2 \cdot {\rm J}_1 \cdot \sin ( \omega_{\rm N} t )\hspace{0.3cm}\Rightarrow \hspace{0.3cm} y_{\rm max} =2 \cdot {\rm J}_1\hspace{0.15cm}\underline { = 1.04}\hspace{0.05cm}, \hspace{0.3cm} y_{\rm min} = -y_{\rm max}\hspace{0.15cm}\underline { = -1.04}\hspace{0.05cm}.$$

(4)  Der Imaginärteil ist zu diesen Zeitpunkten jeweils Null und damit auch die Phasenfunktion:  

$$ϕ(t = n · T_{\rm N}/2)\hspace{0.15cm}\underline{= 0}.$$

• Diesen Sachverhalt erkennt man auch aus der Skizze auf der Angabenseite.

(5)  Aus der Skizze ist bereits zu erkennen, dass der Phasenwinkel beispielsweise für  $t = T_{\rm N}/4$  seinen Maximalwert erreicht.

• Dieser kann mit  $y_{\rm max} = 1.04$  und  $x_{\rm min} = -0.86$  wie folgt berechnet werden:

$$\phi_{\rm max} = \arctan \frac{y_{\rm max}}{x_{\rm min}} = \arctan (-1.21) = 180^\circ - 50.4^\circ \hspace{0.15cm}\underline {= 129.6^\circ} \hspace{0.05cm}.$$

• Ohne Bandbegrenzung würde sich hier der Phasenwinkel  $ϕ(t = T_{\rm N}/4) = η = 2.4 = 137.5^\circ$  ergeben.
• Die maximale Abweichung des Sinkensignals vom Quellensignal tritt somit beispielsweise zur Zeit  $t = T_{\rm N}/4$  auf.

Parabelverlauf

(6)  Mit  $γ = ω_{\rm N} · t$  und  $\cos(2γ) = 1 - 2 · \cos^2(γ)$  kann für Real– und Imaginärteil geschrieben werden:

$$x = {\rm J}_0 + 4 \cdot {\rm J}_2 \cdot \cos^2 (\gamma) - 2 \cdot {\rm J}_2\hspace{0.05cm},\hspace{0.3cm} y = 2 \cdot {\rm J}_1 \cdot \sin (\gamma) \hspace{0.05cm}.$$

• Diese Gleichungen können wie folgt umgeformt werden:

$$\cos^2 (\gamma) =\frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} \hspace{0.05cm},\hspace{0.3cm} \sin^2 (\gamma) = \frac{y^2 }{4 \cdot {\rm J}_1^2}$$

$$\Rightarrow \hspace{0.3cm} \frac{y^2 }{4 \cdot {\rm J}_1^2} + \frac{x-{\rm J}_0 + 2 \cdot {\rm J}_2 }{4 \cdot {\rm J}_2} =1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {y^2 } + \frac{{\rm J}_1^2}{ {\rm J}_2} \cdot x + {{\rm J}_1^2} \cdot \left ( 2 - \frac{{\rm J}_0}{ {\rm J}_2} \right ) =0\hspace{0.05cm}.$$

• Damit lauten die Parabelparameter für  ${\rm J}_0 = 0$:

$$a = \frac{{\rm J}_1^2}{ {\rm J}_2} \hspace{0.15cm}\underline {\approx 0.629}, \hspace{0.3cm} b = 2 \cdot {\rm J}_1^2 \hspace{0.15cm}\underline {\approx 0.541} \hspace{0.05cm}.$$

• Zur Kontrolle verwenden wir  $y = 0$   ⇒   $x_{\rm max} = {b}/{a} = 2 \cdot {\rm J}_2 = 0.86 \hspace{0.05cm}.$
• Die Werte bei  $x = 0$  sind somit:     $y_0 = \pm \sqrt{2} \cdot {\rm J}_1 \approx 0.735 \hspace{0.05cm}.$