Exercise 4.3: Natural and Discrete Sampling

• Return to book

For natural and discrete sampling

Ideal sampling can be described in the time domain by multiplying the analog source signal  $q(t)$  by a  Diracpulse  $p_δ(t)$  :

$$q_{\rm A}(t) = p_{\delta}(t) \cdot q(t) \hspace{0.05cm}.$$

Dirac pulses - infinitely narrow and infinitely high - and accordingly also the Dirac pulse  $p_δ(t)$  cannot be realized in practice, however.  Here we must assume instead the square pulse  $p_{\rm R}(t)$  where the following relation holds:

$$p_{\rm R}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \right ]\star g_{\rm R}(t)\hspace{0.9cm}\text{with}\hspace{0.9cm} g_{\rm R}(t) = \left\{ \begin{array}{l} 1 \ 1/2 \ 0 \ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} < T_{\rm R}/2\hspace{0.05cm}, \ {\hspace{0.04cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} = T_{\rm R}/2\hspace{0.05cm}, \ {\hspace{0.005cm}\left|\hspace{0.06cm} t \hspace{0.05cm} \right|} > T_{\rm R}/2\hspace{0.05cm}. \hspace{0.05cm} \end{array}$$

The duration  $T_{\rm R}$  of a rectangular pulse  $g_{\rm R}(t)$  should be (significantly) smaller than the distance $T_{\rm A}$ of two samples.

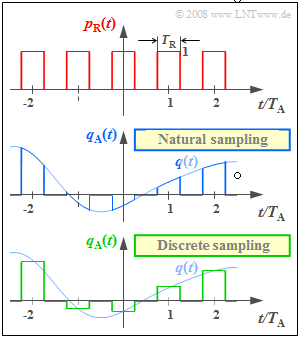
In the diagram this ratio is chosen very large with  $T_{\rm R}/T_{\rm A} = 0.5$  to make the difference between  "natural sampling"  and  "discrete sampling"  especially clear:

• In natural sampling, the sampled signal  $q_{\rm A}(t)$  is equal to the product of square pulse  $p_{\rm R}(t)$  and analog source signal  $q(t)$:

$$q_{\rm A}(t) = p_{\rm R}(t) \cdot q(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t)\hspace{0.05cm}.$$

• In contrast, the corresponding equation for discrete sampling is:

$$q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \cdot q(t)\right ]\star g_{\rm R}(t)\hspace{0.05cm}.$$

In the graph, these signals are sketched in blue  (natural sampling)  and green  (discrete sampling)  respectively.

For signal reconstruction, a rectangular low-pass filter  $H(f)$  with cutoff frequency  $f_{\rm G} = f_{\rm A}/2$  and gain  $T_{\rm A}/T_{\rm R}$  is used in the passband:

$$H(f) = \left\{ \begin{array}{l} T_{\rm A}/T_{\rm R} \ 0 \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \end{array}\begin{array}{*{10}c} {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| < f_{\rm A}/2}\hspace{0.05cm}, \ {\hspace{0.04cm}\left| \hspace{0.005cm} f\hspace{0.05cm} \right| > f_{\rm A}/2}\hspace{0.05cm}. \end{array}$$

Hints:

• The exercise belongs to the chapter  Puls Code Modulation.
• Reference is made in particular to the page  Natural and discrete sampling.
• The sampled source signal is denoted by  $q_{\rm A}(t)$  and its spectral function by  $Q_{\rm A}(f)$.
• Sampling is always performed at  $ν - T_{\rm A}$.

Questions

1

Let  $T_{\rm R}/T_{\rm A} = 0.5$.  For this, give the normalized spectrum  $G_{\rm R}(f)/T_{\rm A}$  What spectral value occurs at  $f = 0$ ?

$G_{\rm R}(f=0)/T_{\rm A} \ = \ $

2

What is the spectrum  $Q_{\rm A}(f)$  in natural sampling?  Suggestions:

	It holds  $Q_{\rm A}(f) = P_{\rm δ}(f) ∗ Q(f)$.
	It holds  $Q_{\rm A}(f) = \big[{\rm δ}(f) - (G_{\rm R}(f)/T_{\rm A})\big] ∗ Q(f)$.
	It holds  $Q_{\rm A}(f) = \big[P_{\rm δ}(f) ∗ Q(f)\big] - (G_{\rm R}(f)/T_{\rm A})$.

3

For natural sampling, is the specified low-pass suitable for interpolation?

	Yes.
	No.

4

What is the spectrum  $Q_{\rm A}(f)$  for discrete sampling?  Suggestions:

	It holds  $Q_{\rm A}(f) = P_{\rm δ}(f) ∗ Q(f)$.
	It holds  $Q_{\rm A}(f) = \big[{\rm δ}(f) - (G_{\rm R}(f)/T_{\rm A})\big] ∗ Q(f)$.
	It holds  $Q_{\rm A}(f) = \big[P_{\rm δ}(f) ∗ Q(f)\big] - (G_{\rm R}(f)/T_{\rm A})$.

5

For discrete sampling, is the specified low-pass suitable for interpolation?

	Yes.
	No.

Solution

Solution

(1)  The spectrum of the square pulse  $g_{\rm R}(t)$  with amplitude  $1$  and duration  $T_{\rm R}$  is:

$$G_{\rm R}(f) = T_{\rm R} \cdot {\rm si}(\pi f T_{\rm R}) \hspace{0.3cm} {\rm with}\hspace{0.3cm} {\rm si}(x) = \sin(x)/x \hspace{0.3cm} \rightarrow \hspace{0.3cm} \frac{G_{\rm R}(f)}{T_{\rm A}} = \frac{T_{\rm R}}{T_{\rm A}} \cdot {\rm si}(\pi f T_{\rm R})$$

$$\rightarrow \hspace{0.3cm} \frac{G_{\rm R}(f = 0)}{T_{\rm A}} =\frac{T_{\rm R}}{T_{\rm A}}\hspace{0.15cm}\underline { = 0.5} \hspace{0.05cm}.$$

(2)  The correct solution is the second suggested solution:

• From the given equation in the time domain, the convolution theorem gives:

$$q_{\rm A}(t) = \left [ \frac{1}{T_{\rm A}} \cdot p_{\rm \delta}(t) \star g_{\rm R}(t)\right ]\cdot q(t) \hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f) = \left [ \frac{1}{T_{\rm A}}\cdot P_{\rm \delta}(f) \cdot G_{\rm R}(f) \right ] \star Q(f) = \left [ P_{\rm \delta}(f) \cdot \frac{G_{\rm R}(f)}{{T_{\rm A}}} \right ] \star Q(f) \hspace{0.05cm}.$$

• The first proposed solution is valid only for ideal sampling  (with a Dirac pulse)  and the last one for discrete sampling.

(3)  The answer is YES:

• Starting from the result of the subtask  (2)  using the spectral function of the Dirac pulse, we obtain.

$$Q_{\rm A}(f) = \left [ P_{\rm \delta}(f) \cdot \frac{G_{\rm R}(f)}{{T_{\rm A}}} \right ] \star Q(f)= \left [ \frac{G_{\rm R}(f)}{{T_{\rm A}}} \cdot \sum_{\mu = -\infty}^{+\infty} \delta(f - \mu \cdot f_{\rm A})\right ] \star Q(f) \hspace{0.05cm}.$$

• When the sampling theorem is satisfied and the low-pass filter is correct, of the infinite convolution products, only the convolution product with  $μ = 0$  lie in the passband.
• Taking into account the gain factor  $T_{\rm A}/T_{\rm R}$  we thus obtain for the spectrum at the filter output:

$$V(f) = \frac{T_{\rm A}}{T_{\rm R}} \cdot \left [ \frac{G_{\rm R}(f = 0)}{{T_{\rm A}} \cdot \delta(f )\right ] \star Q(f)= Q(f) \hspace{0.05cm}.$$

(4)  The last suggested solution is correct.

• Shifting the factor  $1/T_{\rm A}$  to the rectangular pulse, we obtain with discrete sampling using the convolution theorem:

$$q_{\rm A}(t) = \big [ p_{\rm \delta}(t)\cdot q(t) \big ] \star \frac{g_{\rm R}(t)}{T_{\rm A}}\hspace{0.3cm} \Rightarrow \hspace{0.3cm}Q_{\rm A}(f)= \big [ P_{\rm \delta}(f)\star Q(f) \big ] \cdot \frac{G_{\rm R}(f)}{T_{\rm A}}\hspace{0.05cm}.$$

(5)  The answer is NO:

• The weighting function  $G_{\rm R}(f)$  now involves the inner kernel  $(μ = 0)$  of the convolution product.
• All other terms  $(μ ≠ 0)$  are eliminated by the low-pass filter.  One obtains here in the relevant range  $|f| < f_{\rm A}/2$:

$$V(f) = \frac{T_{\rm A}}{T_{\rm R}} \cdot \frac{G_{\rm R}(f )}{{T_{\rm A}}} \cdot Q(f) = 2 \cdot 0.5 \cdot {\rm si}(\pi f T_{\rm R})\cdot Q(f) \hspace{0.3cm}\Rightarrow \hspace{0.3cm}V(f) = Q(f) \cdot {\rm si}(\pi f T_{\rm R})\hspace{0.05cm}.$$

• If no additional equalization is provided here, the higher frequencies are attenuated according to the  $\rm si$ function.
• The highest  signal frequency  $(f = f_{\rm A}/2)$  is attenuated the most here:

$$V(f = \frac{f_{\rm A}}{2}) = Q( \frac{f_{\rm A}}{2}) \cdot {\rm si}(\pi \cdot \frac{T_{\rm R}}{2 \cdot T_{\rm A}})= Q( \frac{f_{\rm A}}{2}) \cdot {\rm si}(\pi \cdot \frac{\sin(\pi/4)}{\pi/4})\approx 0.9 \cdot Q( \frac{f_{\rm A}}{2}) \hspace{0.05cm}.$$