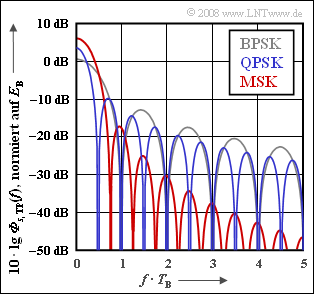
Exercise 4.15: MSK Compared with BPSK and QPSK

Power-spectral densities: BPSK, QPSK, MSK

Verglichen werden die Leistungsdichtespektren (im äquivalenten Tiefpassbereich) von

Binary Phase Shift Keying $\rm (BPSK)$,
Quaternary Phase Shift Keying $\rm (QPSK)$,
Minimum Shift Keying $\rm (MSK)$.

Diese sind in der Grafik logarithmisch dargestellt, wobei die Frequenz auf den Kehrwert der Bitdauer $T_{\rm B}$ normiert ist.

Für die BPSK und die QPSK ist jeweils ein rechteckförmiger Grundimpuls der Höhe $s_0$ und der Symboldauer $T$ vorausgesetzt. Damit gilt für die BPSK und die QPSK (bzw. die 4–QAM und die Offset–QPSK) gleichermaßen:

$${\it \Phi}_{s}(f) = \frac{s_0^2 \cdot T}{4} \cdot \big [ {\rm si}^2 ( \pi T \cdot (f- f_{\rm T}) ) + {\rm si}^2 ( \pi T \cdot (f+ f_{\rm T}) ) \big ]\hspace{0.05cm},$$

und in den äquivalenten Tiefpassbereich transformiert:

$$ {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 ( \pi f T ) \hspace{0.05cm}.$$

Trotz gleicher Formel weisen die BPSK und die QPSK unterschiedliche Leistungsdichtespektren auf:

Bei der BPSK (graue Kurve) ist die Symboldauer $T$ gleich der Bitdauer $T_{\rm B}$ und es gilt mit der Energie pro Bit $(E_{\rm B} = s_0^2 · T_{\rm B}/2)$ :

$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = E_{\rm B} \cdot {\rm si}^2 ( \pi f T_{\rm B} ) \hspace{0.05cm}.$$

Dagegen ist bei der QPSK (blaue Kurve) bei gleichem $E_{\rm B}$ die Symboldauer $T$ doppelt so groß:

$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = 2 \cdot E_{\rm B} \cdot {\rm si}^2 ( 2\pi f T_{\rm B} ) \hspace{0.05cm}.$$

Bei der Berechnung des MSK–Spektrums (rote Kurve) kann berücksichtigt werden, dass die MSK als Offset–QPSK entsprechend dem Block diagram im Theorieteil realisiert werden kann, wenn der folgende Grundimpuls verwendet wird:

$$g(t) = \left\{ \begin{array}{l} g_0 \cdot \cos (\pi/2 \cdot t/T) \\ 0 \\ \end{array} \right.\quad \begin{array}{*{5}c}{\rm{f\ddot{u}r}} \\{\rm{f\ddot{u}r}} \\ \end{array}\begin{array}{*{10}c} -T \le t \le +T \hspace{0.05cm}, \\ {\rm sonst}\hspace{0.05cm}. \\ \end{array}$$

In der Exercise 4.15Z wird die zugehörige Spektralfunktion berechnet:

$$G(f) = \frac {4}{\pi}\cdot g_0 \cdot T \cdot \frac{ {\rm cos} ( 2 \pi f T )}{1 - (4 f T)^2 }\hspace{0.05cm}.$$

Additionally, consider:

Die beiden Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ sind trotz der Vorcodierung unkorreliert.
Bei MSK ist entgegen der QPSK wie bei der BPSK $T = T_{\rm B}$ zu setzen.
Auch bei MSK ist die Energie pro Bit wie folgt gegeben: $E_{\rm B} = s_0^2 · T/2$.
Der Betrag des Tiefpass–Signals $|s_{\rm TP}(t)| = s_0$ ist gleich dem Maximalwert $g_0$ des Grundimpulses $g(t)$.

Hints:

This exercise belongs to the chapter Nonlinear Digital Modulation.
Particular reference is made to the section Realizing MSK as Offset–QPSK.

Das Leistungsdichtespektrums im äquivalenten Tiefpassbereich eines Zweiges – zum Beispiel: Inphasekomponente – lautet:

$${\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = \frac{1}{2 T} \cdot {\rm E} \left [ a_\nu ^2 \right ] \cdot |G(f)|^2 \hspace{0.05cm}.$$

Questions

$f_1 \ = \ $

$\ \cdot 1/T_{\rm B}$

$f_1 \ = \ $

$\ \cdot 1/T_{\rm B}$

${\itΦ}_\text{s, TP}(f = 0) \ = \ $

$\ \cdot E_{\rm B}$

	Die erste LDS–Nullstelle kommt bei MSK früher als bei QPSK.
	Das MSK–Leistungsdichtespektrum klingt schneller ab im Vergleich zur QPSK.
	Bei MSK ist das Integral über ${\itΦ}_\text{s, TP}(f)$ (nicht logarithmiert!) größer als bei QPSK.

Solution

(1) Aus Gleichung und Grafik erkennt man, dass bei Binary Phase Shift Keying $\rm (BPSK)$ die erste Nullstelle des Leistungsdichtespektrums bei $f_1\hspace{0.15cm}\underline{ =1} \cdot 1/T_{\rm B}$ liegt.

(2) Aufgrund der niedrigeren Symbolrate $1/T$ ist bei Quaternary Phase Shift Keying $\rm (QPSK)$ – und bei allen verwandten quaternären Modulationsverfahren – das Spektrum nur halb so breit wie bei der BPSK ⇒ $f_1\hspace{0.15cm}\underline{ =0.5} \cdot 1/T_{\rm B}$.

(3) Für das Leistungsdichtespektrum $\rm (LDS)$ des Gesamtsignals gilt im äquivalenten Tiefpassbereich:

$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f) = {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) + {\it \Phi}_{s,\hspace{0.05cm} {\rm Q},\hspace{0.05cm} {\rm TP}}(f)= 2 \cdot {\it \Phi}_{s,\hspace{0.05cm} {\rm I},\hspace{0.05cm} {\rm TP}}(f) = {1}/{ T} \cdot |G(f)|^2\hspace{0.05cm}.$$

Hierbei ist berücksichtigt, dass

die Signale $s_{\rm I}(t)$ und $s_{\rm Q}(t)$ unkorreliert sind, so dass man die LDS–Anteile addieren kann,
wegen der binären bipolaren Amplitudenkoeffizienten der Erwartungswert $E[a_ν^2] = 1$ ist.

Damit erhält man:

$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{1}{ T} \cdot \left ( \frac {4}{\pi} \right ) ^2 \cdot g_0^2 \cdot T^2 \cdot \frac{ {\rm cos}^2 ( 2 \pi f T )}{ \big [1 - (4 f T)^2 \big ] ^2} \hspace{0.05cm}.$$

Mit $s_0 = g_0$, $T = T_{\rm B}$ und $E_{\rm B} = s_0^2 · T_{\rm B}/2$ gilt weiter:

$${\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f)= \frac{32}{ \pi^2} \cdot E_{\rm B} \cdot \frac{ {\rm cos}^2 ( 2 \pi \cdot f \cdot T_{\rm B} )}{ \big [1 - (4 \cdot f \cdot T_{\rm B})^2 \big ] ^2}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} {\it \Phi}_{s,\hspace{0.05cm} {\rm TP}}(f = 0 )= \frac{32}{ \pi^2} \cdot E_{\rm B} \hspace{0.15cm}\underline {\approx 3.243 \cdot E_{\rm B}} \hspace{0.05cm}.$$

(4) Richtig ist nur der Lösungsvorschlag 1:

Bereits aus der Grafik ist zu ersehen, dass die erste Aussage falsch und die zweite richtig ist.
Der Lösungsvorschlag 3 stimmt ebenfalls nicht. Das Integral über die Leistungsdichtespektren ergibt die Leistung $(E_{\rm B}/T_{\rm B})$.
Die Signalverläufe von BPSK, QPSK und MSK machen deutlich, dass die Leistung bei konstanter Hüllkurve $(s_0)$ für diese drei Modulationsverfahren gleich ist.