Exercise 4.14: ACF and CCF for Square Wave Signals

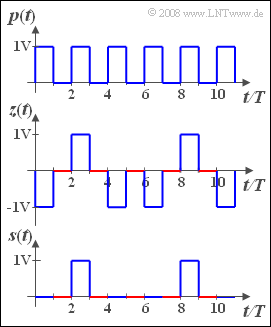
ACF and CCF for rectangular signals

We consider a periodic square wave signal $p(t)$ corresponding to the top sketch with the two possible amplitude values $0 \hspace{0.05cm} \rm V$ and $1 \hspace{0.05cm} \rm V$ and the rectangle duration $T$. Thus, the period duration is $T_0 = 2T$.

Below this is drawn the random signal $z(t)$:

This is $z(t)=0 \hspace{0.05cm} \rm V$ between $(2i-1)\cdot T$ and $2i \cdot T$ respectively (highlighted in red in the figure).
In the intervals drawn in blue between $2i \cdot T$ and $(2i+1) \cdot T$ the signal value is two-point distributed $(\pm 1 \hspace{0.05cm} \rm V)$.

The probability that in the intervals shown in blue $z(t)=+1 \hspace{0.05cm} \rm V$ holds is generally equal $p$ and independent of the previously selected values.

The lowest signal in the adjacent graph can be constructed from the first two. It holds:

$$s(t) = {1}/{2} \cdot \big[p(t) + z(t)\big].$$

In the time intervals drawn in red between $(2i-1) \cdot T$ and $2i \cdot T$ $(i$ integer$)$ holds $s(t)=0 \hspace{0.05cm} \rm V$, since here both $p(t)$ and $z(t)$ are equal to zero.
In the intervening intervals, the amplitude value is two-point distributed between $0 \hspace{0.05cm} \rm V$ and $1 \hspace{0.05cm} \rm V$, where the value $1 \hspace{0.05cm} \rm V$ occurs again with probability $p$.
Or in other words: The signals $z(t)$ and $s(t)$ are equivalent pattern signals of the identical random process with bipolar $(-1 \hspace{0.05cm} \rm V, \ +1 \hspace{0.05cm} \rm V)$ resp. unipolar $(0 \hspace{0.05cm} \rm V, \ 1 \hspace{0.05cm} \rm V)$ signal representation.

Hints:

The exercise belongs to the chapter Cross-Correlation Function and Cross Power Density.
Refer is also made to the chapter Auto-Correlation Function.
Sketch the sought correlation functions in each case in the range from $-7T$ to $+7T$.

Questions

$\varphi_z(\tau= 0) \ = \ $

$\ \rm V^2$

$\varphi_z(\tau= 3T) \ = \ $

$\ \rm V^2$

$\varphi_z(\tau= 6T) \ = \ $

$\ \rm V^2$

$\varphi_p(\tau= 0) \ = \ $

$\ \rm V^2$

$\varphi_p(\tau= 3T) \ = \ $

$\ \rm V^2$

$\varphi_p(\tau= 6T) \ = \ $

$\ \rm V^2$

$\varphi_{pz}(\tau= 0) \ = \ $

$\ \rm V^2$

$\varphi_{pz}(\tau= 3T) \ = \ $

$\ \rm V^2$

$\varphi_{pz}(\tau= 6T) \ = \ $

$\ \rm V^2$

	$\varphi_c(\tau) = \varphi_a(\tau) + \varphi_b(\tau)$.
	$\varphi_c(\tau) = \varphi_a(\tau) + \varphi_{ab}(\tau) + \varphi_{ba}(\tau) + \varphi_b(\tau)$.
	$\varphi_c(\tau) = \varphi_a(\tau) \star \varphi_b(\tau)$.

$\varphi_s(\tau= 0) \ = \ $

$\ \rm V^2$

$\varphi_s(\tau= 3T) \ = \ $

$\ \rm V^2$

$\varphi_s(\tau= 6T) \ = \ $

$\ \rm V^2$

Solution

(1) The ACF value at $\tau = 0$ gives the average power:

$$\varphi_z ( \tau = 0) = {1}/{2} \cdot (1 {\rm V})^2 \hspace{0.15cm}\underline{= 0.5 {\rm V}^2}.$$

For $\tau = \pm T$, $\underline{\tau = \pm 3T}$, ... results $\varphi_z ( \tau)\hspace{0.15cm}\underline{ = 0}$.

For intermediate values $\tau = \pm 2T$, $\tau = \pm 4T$, $\underline{\tau = \pm 6T}$, ... applies:

$$\varphi_z ( \tau) = \frac {1 {\rm V}^2}{2} \left(p \hspace{0.02cm} \cdot \hspace{0.02cm}p \hspace{0.2cm} + \hspace{0.2cm}p \hspace{0.02cm}\cdot \hspace{0.02cm}(p-1) \hspace{0.2cm}+\hspace{0.2cm} (p-1)\hspace{0.02cm} \cdot \hspace{0.02cm}p \hspace{0.2cm}+\hspace{0.2cm} (p-1)\hspace{0.02cm} \cdot \hspace{0.02cm}(p-1)\right) = \hspace{0.1cm}\text{...} \hspace{0.1cm}= 0.5\, {\rm V}^2 \cdot (1-2p)^2 .$$

Auto-correlation functions and cross-correlation function

Here $p$ stands for $p \cdot (+1)$ and $(p-1)$ for $(1-p) \cdot (-1)$, i.e. probability times normalized amplitude value, respectively.
With $p = 0.25$ one gets $\varphi_z ( \tau = \pm 6 T) \hspace{0.15cm}\underline{=0.125 \rm V^2}$.

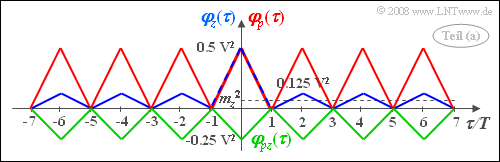
The blue curve shows $\varphi_z(\tau)$ for $p = 0.25$ in the range of $-7T \le \tau \le +7T$:

Because of the rectangular signal waveform, a sum of triangular functions is obtained.
For $p = 0.5$ the äußeren (smaller) triangles would disappear.

(2) The ACF $\varphi_p(\tau)$ of the unipolar periodic signal $p(t)$ is in the generalized representation of (1) ⇒ ACF $\varphi_z(\tau)$ as a special case for $p = 1$ .

Now one obtains a periodic ACF (see red curve in the above sketch) with

$$\varphi_p ( \tau = 0) = \varphi_p ( \tau = \pm 2 T) = \varphi_p ( \tau = \pm 4 T) = \hspace{0.1cm} \text{...} \hspace{0.1cm}\hspace{0.15cm}\underline{= 0.5 {\rm V}^2},$$

$$\varphi_p ( \tau = \pm T) = \varphi_p ( \tau = \pm 3T) = \hspace{0.1cm} ... \hspace{0.1cm}\hspace{0.15cm}\underline{= 0}.$$

(3) Also für the cross-correlation function results for $\tau = \pm T$, $\underline{\tau = \pm 3T}$, ... always the value zero.

In contrast, the CCF values for $\tau = \pm 2T$, $\tau = \pm 2T$, ... identical to those for $\tau = 0$:

$$\varphi_{pz} ( \tau = 0) = \varphi_{pz} ( \tau = \pm 2 T) = \varphi_{pz} ( \tau = \pm 4 T) = \hspace{0.1cm} \text{...} \hspace{0.1cm}= \frac {1 {\rm V}^2}{2} \left( p - (1-p)\right) = \frac {2p -1}{2}\, {\rm V}^2 .$$

You get the following results with $p = 0.25$ (see green curve in above sketch):

$$\varphi_{pz} ( \tau = 0)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2},\hspace{0.5cm} \varphi_{pz} ( \tau = 3T)\hspace{0.15cm}\underline{= 0},\hspace{0.5cm} \varphi_{pz} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.25 {\rm V}^2}.$$

With $p = 1$ on the other hand $z(t) \equiv p(t)$ would hold and so of course $\varphi_{pz}(\tau) \equiv \varphi_{p}(\tau) \equiv \varphi_{z}(\tau)$.
For the special case $p = 0.5$ there would be no correlation between $p(t)$ and $z(t)$ and thus $\varphi_{pz}(\tau) \equiv 0$.

(4) Substituting $c(t) = a(t) + b(t)$ into the general ACF definition yields:

$$\varphi_c ( \tau ) = \overline{c(t)\hspace{0.02cm} \cdot \hspace{0.02cm} c(t + \tau)} = \overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} a(t + \tau)} \hspace{0.1cm}+\hspace{0.1cm}\overline{a(t)\hspace{0.02cm} \cdot \hspace{0.02cm} b(t + \tau)} +\overline{b(t)\hspace{0.02cm} \cdot \hspace{0.02cm} a(t + \tau)} \hspace{0.1cm}+\hspace{0.1cm}\overline{b(t)\hspace{0.02cm} \cdot \hspace{0.02cm} b(t + \tau)}. $$

$$\Rightarrow \hspace{0.5cm} \varphi_c ( \tau ) = \varphi_{a} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ab} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{ba} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm}\varphi_{a} ( \tau ). $$

The correct solution is thus the proposed solution 2.
The proposed solution 1 is true only if $a(t)$ and $b(t)$ are uncorrelated.
The last proposition, the convolution operation, is always false.
A similar equation would result only if we consider the WDF $f_c(c)$ of the sum $c(t) = a(t) + b(t)$ and $a(t)$ and $b(t)$ are statistically independent: $f_c (c) = f_a (a) \star f_b (b) .$

(5) Using the result from (4) and taking into account the factor $1/2$ we get:

$$\varphi_s ( \tau ) = {1}/{4} \cdot \big[ \varphi_{p} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} \varphi_{z} ( \tau ) \hspace{0.1cm} + \hspace{0.1cm} 2 \cdot \varphi_{pz} ( \tau ) \big] . $$

This already takes into account that the PPF between $p(t)$ and $z(t)$ is an even function, so that also $\varphi_{pz}(\tau) = \varphi_{zp}(\tau)$ holds.
For $\tau = 0$ one therefore obtains in general with the above results:

$$\varphi_s( \tau = 0) = {1}/{4} \cdot \left( 0.5 {\rm V}^2 +0.5 {\rm V}^2 + 2 \cdot \frac{2p-1}{2} {\rm V}^2\right) .$$

With $p = 0.25$ we get $\varphi_{pz} ( \tau = 0 ) = 0.125\rm V^2$. This result is plausible. On average, only in every eighth interval $s(t)=1 \hspace{0.05cm} \rm V$; otherwise $s(t)=0 \hspace{0.05cm} \rm V$.

For even multiples of $T$ holds:

$$ \varphi_s ( \tau = \pm 2 T) = \varphi_s ( \tau = \pm 4 T) = \hspace{0.1cm} \text{ ...} \hspace{0.1cm} = \frac {0.5 {\rm V}^2}{4} \left( (1-2p)^2 +1 + 2 \cdot (2p -1)\right) = 0.5 \, {\rm V}^2 \hspace{0.02cm} \cdot \hspace{0.02cm} p^2.$$

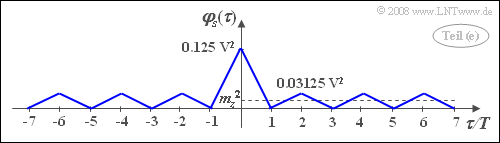
With $p = 0.5$ we obtain for this the value $0.03125 \hspace{0.1cm}{\rm V}^2$. All ACF values at odd multiples of $T$ are zero again.
This gives the outlined ACF–curve.

ACF of a unipolar rectangular signal

Thus, the numerical values we are looking for are:

$$\varphi_{s} ( \tau = 0)\hspace{0.15cm}\underline{= 0.125 {\rm V}^2},$$

$$\varphi_{s} ( \tau = 3T)\hspace{0.15cm}\underline{= 0},$$

$$\varphi_{s} ( \tau = 6T)\hspace{0.15cm}\underline{= -0.03125 {\rm V}^2}.$$

A comparison with the sketch for the subtask (1) shows that the binary signal $s(t)$ has the same ACF as the ternary signal $z(t)$ except for the factor $1/4$ .