Exercise 4.5: Non-Linear Quantization

PCM system with companding

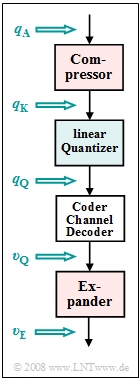
To investigate nonlinear quantization we start from the outlined system model.

We disregard the influence of the channel and the PCM coding or decoding.
Thus, $v_{\rm Q}(ν \cdot T_{\rm A}) = q_{\rm Q}(ν \cdot T_{\rm A})$ always applies, whereby the time specification $ν \cdot T_{\rm A}$ is omitted in the following.

By comparing one output variable with one input variable at a time, it is possible to determine the influence

of the compressor ⇒ $q_{\rm K}(q_{\rm A})$,
of the linear quantizer ⇒ $q_{\rm Q}(q_{\rm K})$,
of the nonlinear quantizer ⇒ $q_{\rm Q}(q_{\rm A})$,
of the expander ⇒ $v_{\rm E}(v_{\rm Q})$, and
of the overall system ⇒ $v_{\rm E}(q_{\rm A})$

The following assumptions are made:

All samples $q_{\rm A}$ are in the range of values $±1$ .
The (linear) quantizer works with $M = 256$ quantization levels, which are marked with $μ = 0$ to $μ = 255$ .
For compression, the so-called 13-segment characteristic is used.

This means:

In the range $|q_{\rm A}| ≤ 1/64$ holds $q_{\rm K} = q_{\rm A}$.
For $q_{\rm A} > 1/64$ , $k = 1$, ... , $6$ the following six additional ranges of the compressor characteristic:

$$q_{\rm K}(q_{\rm A}) = 2^{4-k} \cdot q_{\rm A} + {k}/{8}\hspace{0.9cm} {\rm im\,\,range}\hspace{0.9cm}2^{k-7}< q_{\rm A} \le 2^{k-6} \hspace{0.05cm}.$$

Another six domains exist for the negative $q_{\rm A}$ values with $k = -1$, ... , $-6$, which are point-symmetric with respect to the origin.
However, these are not considered further in this exercise.

Hints:

The task belongs to the chapter Pulse code modulation.
Reference is made in particular to the page Compression and Expansion.

Questions

$q_{\rm K} \ = \ $

$\mu \ = \ $

$q_{\rm Q} \ = \ $

$v_{\rm E} \ = \ $

	The characteristic $q_{\rm Q}(q_{\rm A})$ approximates the compressor characteristic in steps.
	The characteristic $q_{\rm Q}(q_{\rm A})$ approximates the angle bisector in steps.
	The step width is the same in all segments $($except for $k = 0)$ .
	The step height is equal in all segments $($except for $k = 0)$ .

	The characteristic $v_{\rm E}(q_{\rm A})$ approximates the compressor characteristic in steps.
	The characteristic $v_{\rm E}(q_{\rm A})$ approximates the angle bisector in steps.
	The step width is the same in all segments $($except for $k = 0)$ .
	The step height is equal in all segments $($except for $k = 0)$ .

Solution

(1) The sample $q_{\rm A} = 0.4$ belongs to the segment $k = 5$ covering the range $1/4 < q_{\rm A} ≤ 1/2$ From the given equation it follows that with $k = 5$:

$$q_{\rm K}(q_{\rm A}) = 2^{4-k} \cdot q_{\rm A} + {k}/{8}={1}/{2}\cdot 0.4 + {5}/{8} \hspace{0.15cm}\underline {= 0.825}\hspace{0.05cm}.$$

(2) The input value of the linear quantizer is now $q_{\rm K} = 0.825$, so the following calculation applies:

$${105}/{128} < q_{\rm K} = 0.825 \le {106}/{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 105 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 105\hspace{0.15cm}\underline { = 233} \hspace{0.05cm}.$$

(3) According to the specification page, the quantization interval $μ = 128 + m$ is given by the value $q_{\rm Q} = 1/256 + m/128$ represented. With $m = 105$ it follows:

$$q_{\rm Q} = \frac{1}{256} + \frac{105}{128} \hspace{0.15cm}\underline {\approx 0.824} \hspace{0.05cm}.$$

(4) According to the sample solution to the subtask (3) with the input value $q_{\rm A} = 0.04$:

$$ \frac{1}{32} < q_{\rm A} \frac{1}{16}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} k = 2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} q_{\rm K} = 2^2 \cdot 0.04 + \frac{2}{8}= 0.41$$

$$\Rightarrow \hspace{0.3cm}\frac{52}{128} < q_{\rm K} = 0.41 \le \frac{53}{128}\hspace{0.3cm}\Rightarrow \hspace{0.3cm} m = 52 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} \mu = 128 + 52 = 180\hspace{0.3cm} \Rightarrow \hspace{0.3cm}q_{\rm Q} = \frac{1}{256} + \frac{52}{128} \hspace{0.15cm}\underline {= 0.41} \hspace{0.05cm}.$$

characteristics of compressor (blue) and expander (green)

(5) We are looking for the solution in several steps:

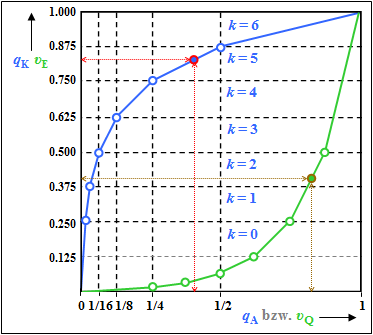
In the compressor has $q_{\rm A} = 0.4$ led to the initial value $q_{\rm K} = 0.825$ and after quantization to the value $q_{\rm Q} = 0. 824$– see subtasks (1) and (3). Note the red marks in the graph.
The graph shows that, on the receiver side, this results in $v_{\rm Q} = 0.824$ approximately back to $v_{\rm E} ≈ 0.4$ ⇒ brown marks in the graph.

However, due to quantization, this is only an approximation. Exactly:

$$ v_{\rm E} = 0.25 + \frac{0.824-0.750}{0.875-0.750} \cdot 0.25 \hspace{0.15cm}\underline {= 0.398} \hspace{0.05cm}.$$

This calculation process can be understood from the graph. Although the expander characteristic $v_E(υ_{\rm Q})$ is equal to the inverse function of the compressor characteristic $q_K(q_{\rm A})$ an error results because the input $v_{\rm Q}$ of the expander is discrete in value (influence of quantization).

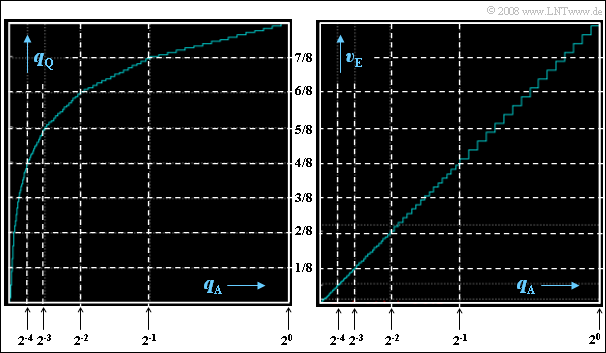
(6) Correct are statements 1 and 4, as can be verified by the following left graph:

13-segment characteristic curves: left: $q_{\rm Q}(q_{\rm A})$, right: $v_{\rm E}(q_{\rm A})$

The width of each step is different in each segment.
In the outermost segment $(k = 6)$ the step width is $0.5/16 = 1/32$, in the next segment $(k = 5)$ only more $0.25/16 = 1/64$.
The step widths in the further segments are $1/128 \ (k = 4)$, $1/256 \ (k = 3)$, $1/512\ (k = 2)$ and $1/1024 \ (k = 1)$.
The innermost range from $-1/64$ to $+1/64$ is divided into $64$ steps, resulting in the step width $1/2048$ .
The step height, on the other hand, is constantly equal $1/8$ divided by $16 = 1/128$ in the segments $k ≠ 0$ and equal $1/256$ in the middle segment.

(7) Correct here is only the second statement:

By the expander, the quantization is now along the bisector of the angle.
In each segment, step width and step height are constant.
As the right graphic shows, however, in the next inner segment the width and the height are only half as large.