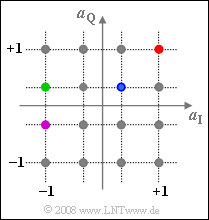
Exercise 4.10Z: Signal Space Constellation of the 16-QAM

• Return to book

Signal space constellation

We now consider the 16-QAM method according to the block diagram given in the theory section.  The diagram shows the possible complex amplitude coefficients  $a = a_{\rm I} + {\rm j} · a_{\rm Q}$.

As in  Exercise 4.10,  the following should be assumed:

• The possible amplitude coefficients  $a_{\rm I}$  and  $a_{\rm Q}$  of the two component signals are $ ±1$  and  $±1/3$, respectively.
• The basic transmission pulse  $g_s(t)$  is rectangular with amplitude  $g_0 = 1\ \rm V$  and duration  $T = 1 \ \rm µ s$.
• The source signal  $q(t)$  before the serial-to-parallel converter is binary and redundancy-free.

Hints:

• This exercise belongs to the chapter   "Quadrature Amplitude Modulation".
• The page  "Quadratic QAM signal space constellations"  is helpful for completing this exercise.
• The signals belonging to the colored points are shown in the same colors as in  Exercise 4.10.

Questions

1

What is the bit rate  $R_{\rm B}$  of the binary source signal  $q(t)$?

$R_{\rm B}\ = \ $ $\ \rm Mbit/s$

2

Give the magnitude and the phase  $($between  $±180^\circ)$  for the red symbol   ⇒   $a = 1 +{\rm j}$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm degrees$

3

Give the magnitude and the phase for the blue symbol   ⇒   $a = 1/3 +{\rm j}/3$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm degrees$

4

Give the magnitude and the phase for the green symbol  ⇒   $a = -1 +{\rm j}/3$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm degrees$

5

Give the magnitude and the phase for the purple symbol  ⇒   $a = -1 -{\rm j}/3$.

$|a| \ = \ $

${\rm arc} \ a \ = \ $ $\ \rm degrees$

6

How many different magnitudes   ⇒   $N_{|a|}$  and phase positions   ⇒   $N_{arc}$ are possible?

$N_{|a|}\ = \ $

$N_{\rm arc}\ = \ $

Solution

Solution

(1)  Each   $\log_2 \ 16 = 4$  bits of the source signal are represented by one symbol, two bits by the four-level coefficient   $a_{\rm I}$  and two more by  $a_{\rm Q}$.

• Thus, the bit time is  $T_{\rm B} = T/4 = 0.25 \ \rm µ s$.
• And the bit rate is then  $R_{\rm B} = 1/T_{\rm B}\hspace{0.15cm}\underline { = 4 \ \rm Mbit/s}$.

(2)  From geometry, for   $a = 1 + {\rm j}$ it follows:

$$a| = \sqrt{1^2 + 1^2}= \sqrt{2}\hspace{0.15cm}\underline { =1.414}\hspace{0.05cm}, \hspace{0.5cm} {\rm arc}\hspace{0.15cm} a = \arctan \left ({1}/{1} \right ) \hspace{0.15cm}\underline {= 45^{\circ}}\hspace{0.05cm}.$$

(3)  The angle is obtained as in subtask   (2), the magnitude is smaller by a factor of   $3$ :

$$|a| = \sqrt{(1/3)^2 + (1/3)^2}= \sqrt{2}\hspace{0.15cm}\underline { =0.471}\hspace{0.05cm}, \hspace{0.5cm} {\rm arc}\hspace{0.15cm} a \hspace{0.15cm}\underline {= 45^{\circ}}\hspace{0.05cm}.$$

(4)  For the complex amplitude coefficient  $a = -1 + {\rm j}/3$  geometry gives us:

$$|a| = \sqrt{1^2 + (1/3)^2}\hspace{0.15cm}\underline {= 1.054}\hspace{0.05cm},\hspace{0.5cm} {\rm arc}\hspace{0.15cm} a = 180^{\circ} - \arctan \left ( {1}/{3} \right ) = 180^{\circ} - 18.43^{\circ} \hspace{0.15cm}\underline {= 161.57^{\circ}}\hspace{0.05cm}.$$

(5)  The purple symbol  $a = -1 - {\rm j}/3$  has the same magnitude as the green symbol according to subtask   (4), while the phase angle changes sign:

$$|a| \hspace{0.15cm}\underline {= 1.054}\hspace{0.05cm},\hspace{0.5cm} {\rm arc}\hspace{0.15cm} a \hspace{0.15cm}\underline {= -161.57^{\circ}}\hspace{0.05cm}.$$

(6)  For the magnitude  $N_{|a|}\hspace{0.15cm}\underline { = 3}$  different results are possible:  $1.414$,  $1.054$  and  $0.471$.

• In contrast, there are   $N_{\rm arc}\hspace{0.15cm}\underline { = 12}$  possible phase positions, namely:

$$ \pm \arctan (1/3) = \pm 18.43^{\circ}, \hspace{0.2cm}\pm \arctan (1) = \pm 45^{\circ}, \hspace{0.2cm}\pm \arctan (3) = \pm 71.57^{\circ}\hspace{0.05cm},$$

$$\pm (180^{\circ}-71.57^{\circ}) = \pm 108.43^{\circ}, \hspace{0.2cm}\pm (180^{\circ}-45^{\circ}) = \pm 135^{\circ}, \hspace{0.2cm}\pm 161.57^{\circ} \hspace{0.05cm}.$$