Exercise 2.7Z: Power-Spectral Density of Pseudo-Ternary Codes
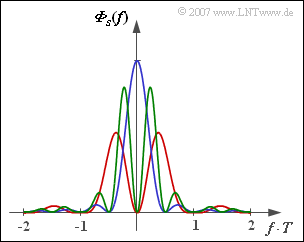
In the graph you can see the power-spectral densities of three different pseudo ternary codes, which result from the general description according to Aufgabe 2.7 by different values of the parameters $N_{\rm C}$ and $K_{\rm C}$. In different colors the power-spectral densities
- $${\it \Phi}_s(f) 0 \ \frac{s_0^2 \cdot T}{2} \cdot {\rm si}^2 (\pi f T) \cdot \big [1 - K_{\rm C} \cdot \cos (2\pi f N_{\rm C} T)\big ]$$
are shown for the following variants:
- AMI code $(N_{\rm C} = 1, K_{\rm C} = +1)$,
- duobinary code $(N_{\rm C} = 1, K_{\rm C} = -1)$,
- second order bipolar code $ (N_{\rm C} = 2, K_{\rm C} = +1)$.
The above PSD equation assumes the use of rectangular NRZ basic transmission pulses.
All pseudo ternary codes considered here have the same probability distribution:
- $${\rm Pr}\big[s(t) = 0\big]= {1}/{2},\hspace{0.2cm}{\rm Pr}\big[s(t) = +s_0\big]= {\rm Pr}\big[s(t) = -s_0\big]={1}/{4}\hspace{0.05cm}.$$
Notes:
- The exercise belongs to the chapter Symbol-Wise Coding with Pseudo Ternary Codes.
- You can check the results with the interactive applet Signals, ACF and PSD of pseudo ternary codes.
Questions
Solution
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
This curve shape is shown in red. The PSD of the amplitude coefficients is ${\it \Phi}_{a}(f) = \sin^2(\pi fT)$.
(2) After reshaping, we obtain for the duobinary code:
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \cos^2 (\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
In the graph, the duobinary code is drawn in blue. Furthermore, ${\it \Phi}_{a}(f) = \cos^2(\pi fT)$.
(3) The second order bipolar code differs from the AMI code only by the factor $2$ in the argument of the $\sin^{2}$ function:
- $${\it \Phi}_s(f) = {s_0^2 \cdot T} \cdot \sin^2 (2\pi f T) \cdot {\rm si}^2 (\pi f T) \hspace{0.05cm}.$$
The green curve represents this function progression. Compared to AMI code, ${\it \Phi}_{a}(f)$ is exactly half as wide.
(4) The transmit power $P_{\rm S}$ is equal to the integral over the power-spectral density ${\it \Phi}_{s}(f)$ and is the same for all codes considered here ⇒ solution 4.
- This also follows from the power calculation by coulter averaging:
- $$P_{\rm S} = \ {\rm Pr}[s(t) = +s_0] \cdot (+s_0)^2 + {\rm Pr}[s(t) = -s_0] \cdot (-s_0)^2= {1}/{4}\cdot s_0^2 + {1}/{4}\cdot s_0^2 = {1}/{2}\cdot s_0^2\hspace{0.05cm}.$$
(5) Solutions 1 and 3 are correct:
- Equal signal freedom exists if the power-spectral density has no component at frequency $f = 0$.
- This is true for the AMI code and the second order bipolar code.
- This statement does not only mean that $s(t)$ has no DC component, i.e. that ${\it \Phi}_{s}(f)$ has no Dirac delta function at $f = 0$.
- Moreover, it also means that the continuous PSD component vanishes at $f = 0$.
- This is achieved exactly when both the long "$+1$" and the long "$–1$" sequences are excluded by the coding rule.
(6) Both solutions apply in practice.