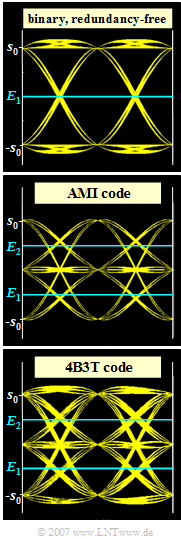
Exercise 2.8: Code Comparison: Binary, AMI and 4B3T
In the graphic three eye diagrams (without noise) are shown, where in each case a rectangular NRZ basic transmission pulse and for the total system frequency response (of transmitter, channel and decoder, without encoder) a cosine rolloff characteristic with rolloff factor $r = 0.8$ are the basis.
For the individual eye diagrams it is furthermore assumed (from top to bottom):
- the redundancy-free binary code,
- the AMI code (approx. $37 \%$ redundancy),
- the 4B3T code (approx. $16 \%$ redundancy).
Further, the following conditions can be assumed:
- AWGN noise is present, where holds:
- $$10 \cdot {\rm lg}\hspace{0.1cm} ({s_0^2 \cdot T}/{N_0}) = 10\, {\rm dB}\hspace{0.05cm}.$$
- The detection noise power has the following value for the binary system (due to the non-optimal receiver filter $12 \%$ markup):
- $$\sigma_d^2 = 1.12 \cdot {N_0}/({2 T})\hspace{0.05cm}.$$
- The symbol error probability of the binary system is:
- $$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right) \hspace{0.05cm}.$$
- In contrast, for the two redundant pseudo-ternary systems:
- $$p_{\rm S} = {4}/{3} \cdot {\rm Q} \left( s_0/(2 \sigma_d) \right) \hspace{0.05cm}.$$
- It should be taken into account that the noise rms value $\sigma_{d}$ may well change with respect to the redundancy-free binary system.
Notes:
- The exercise belongs to the chapter "Symbolwise Coding with Pseudo- Ternary Codes".
- Reference is also made to the chapter "Block Coding with 4B3T Codes".
- For numerical evaluation of the Q-function you can use the HTML5/JavaScript applet "Complementary Gaussian Error Functions".
Questions
Solution
- $$10 \cdot {\rm lg}\hspace{0.1cm}({s_0^2 \cdot T}/{N_0}) = 10\, {\rm dB} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{N_0} = { s_0^2 \cdot T}/{10}$$
- $$ \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma_d^2 = 1.12 \cdot {N_0}/({2 T}) = 0.056 \cdot s_0^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}{ \sigma_d}/{s_0} \hspace{0.15cm}\underline { = 0.237}\hspace{0.05cm}.$$
(2) From this, it follows for the symbol error probability of the binary redundancy-free reference system:
- $$p_{\rm S} = {\rm Q} \left( {s_0}/{ \sigma_d} \right)\approx {\rm Q}(4.22)\hspace{0.15cm}\underline { = 1.22 \cdot 10^{-5}} \hspace{0.05cm}.$$
(3) The symbol duration $T$ of the AMI encoded signal is equal to the bit duration $T_{\rm B}$ of the binary signal. Therefore, the bandwidth ratios do not change and the same noise rms value is obtained as calculated in point (1):
- $${ \sigma_d}/{s_0}\hspace{0.15cm}\underline { = 0.237} \hspace{0.05cm}.$$
(4) Due to the ternary decision, the argument of the Q-function is halved:
- $$p_{\rm S} \approx{4}/{3}\cdot {\rm Q}(2.11)={4}/{3} \cdot 1.74 \cdot 10^{-2}\hspace{0.15cm}\underline { = 2.32 \cdot 10^{-2}} \hspace{0.05cm}.$$
Here, the factor $4/3$ takes into account that the inner symbol $0$ can be distorted in two directions.
(5) When a 4B3T coding is applied, the symbol rate is reduced by $25 \%$. By the same factor $0.75$, this makes the noise power smaller than calculated in (1) and (3). From this follows:
- $${ \sigma_d}/{s_0} = \sqrt{0.75} \cdot 0.237 \hspace{0.15cm}\underline {\approx 0.205} \hspace{0.05cm}.$$
(6) Due to the smaller noise rms value, the error probability is now smaller than with the AMI code:
- $$p_{\rm S} \approx {4}/{3} \cdot {\rm Q} \left( \frac{0.5}{ 0.205} \right) = {4}/{3} \cdot 0.833 \cdot 10^{-2}\hspace{0.15cm}\underline { = 1.11 \cdot 10^{-2}} \hspace{0.05cm}.$$
However, the 4B3T code cannot achieve the significantly smaller error probability of the redundancy-free binary code due to the ternary decision (half eye opening).