Properties of Coaxial Cables

Übertragungsmaß von Koaxialkabeln

Koaxialkabel bestehen aus einem Innenleiter und – durch ein Dielektrikum getrennt – einem Außenleiter. Es wurden zwei unterschiedliche Kabeltypen standardisiert, wobei zur Kennzeichnung die Durchmesser von Innen– und Außenleiter herangezogen werden:

das Normalkoaxialkabel, dessen Innenleiter einen Durchmesser von 2.6 mm besitzt und der Außendurchmesser 9.5 mm beträgt,
das Kleinkoaxialkabel mit den Abmessungen 1.2 mm und 4.4 mm.

Der Kabelfrequenzgang $H_{\rm K}(f)$ ergibt sich aus der Kabellänge $l$ und dem Übertragungsmaß $$\gamma(f) = \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot (\beta_1 \cdot f + \beta_2 \cdot \sqrt {f})\hspace{0.05cm}$$ $$\Rightarrow \hspace{0.3cm}H_{\rm K}(f) = {\rm e}^{-\gamma(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{-\alpha(f)\hspace{0.05cm} \cdot \hspace{0.05cm} l}\hspace{0.05cm}.$$

Die kabelspezifischen Konstanten für das Normalkoaxialkabel 2.6/9.5 mm sind: $$\begin{align*}\alpha_0 & = 0.00162\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000435\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.2722\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 21.78\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.2722\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$

Entsprechend lauten die kilometrischen Dämpfungs– und Phasenkonstanten für das Kleinkoaxialkabel: $$\begin{align*}\alpha_0 & = 0.00783\, \frac{ {\rm Np} }{ {\rm km} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_1 = 0.000443\, \frac{ {\rm Np} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \alpha_2 = 0.5984\, \frac{ {\rm Np} }{ {\rm km \cdot \sqrt{MHz} } }\hspace{0.05cm}, \\ \beta_1 & = 22.18\, \frac{ {\rm rad} }{ {\rm km \cdot MHz} }\hspace{0.05cm}, \hspace{0.2cm} \beta_2 = 0.5984\, \frac{ {\rm rad} }{ {\rm km \cdot \sqrt{MHz} } } \hspace{0.05cm}.\end{align*}$$

Diese Werte können aus den geometrischen Abmessungen der Kabel berechnet werden und wurden durch Messungen am Fernmeldetechnischen Zentralamt in Darmstadt bestätigt – siehe $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=entitaet&e_id=29656&hyperlink_typ=entitaet_verweis&session_id=7761LSYGTN1463149483}{[Wel77]}$. Sie gelten für eine Temperatur von 20°C (293 K) und Frequenzen größer als 200 kHz. Es besteht folgender Zusammenhang zu den $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=2433&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=7761LSYGTN1463149483}{Leitungsbelägen}$:

Die vom frequenzunabhängigem Anteil $R’$ herrührenden Ohmschen Verluste werden durch $α_0$ modelliert und verursachen eine (bei Koaxialkabeln geringe) frequenzunabhängige Dämpfung.
Der Anteil $α_1 · f$ des Dämpfungsmaßes ist auf die Ableitungsverluste $(G’)$ zurückzuführen und der frequenzproportionale Term $β_1 · f$ bewirkt nur eine Phasenlaufzeit, aber keine Verzerrungen.
Die Anteile $α_2$ und $β_2$ gehen auf den Skineffekt zurück, der bewirkt, dass bei höherfrequentem Wechselstrom die Stromdichte im Leiterinneren niedriger ist als an der Oberfläche. Dadurch steigt der Widerstandsbelag $R’$ einer elektrischen Leitung mit der Wurzel aus der Frequenz an.

Charakteristische Kabeldämpfung (1)

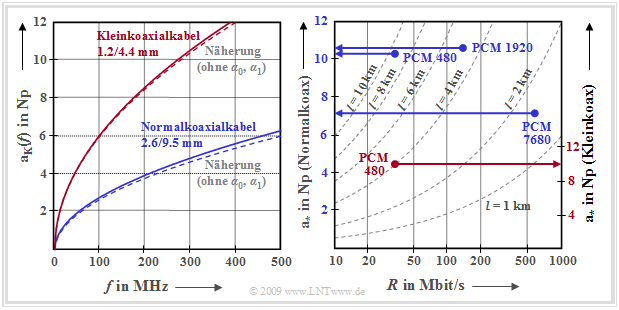
Wir betrachten zunächst die linke Grafik; das rechte Diagramm wird weiter unten beschrieben. Links dargestellt ist das Dämpfungsmaß der zwei Koaxialkabeltypen im Frequenzbereich bis 500 MHz: $${\rm a}_{\rm K}(f) =\left [ \alpha_0 + \alpha_1 \cdot f + \alpha_2 \cdot \sqrt {f} \hspace{0.05cm} \right ] \cdot l \hspace{0.05cm}.$$ Die Ordinatenbeschriftung ist hierbei in Np/km angegeben. Oft erfolgt sie auch in dB/km, wobei die Umrechnung 1 dB = ln(10)/20 = 0.11513 Np gilt.

Man erkennt aus dieser Darstellung, dass der Fehler bei Vernachlässigung des frequenzunabhängigen Anteils $α_0$ und des frequenzproportionalen Terms $(α_1f)$ noch tolerabel ist. Im Folgenden gehen wir deshalb von der folgenden vereinfachten Dämpfungsfunktion aus: $${\rm a}_{\rm K}(f) = \alpha_2 \cdot \sqrt {f} \cdot l = {\rm a}_{\rm \star}\cdot \sqrt { {2f}/{R}} \hspace{0.3cm}\Rightarrow \hspace{0.3cm}|H_{\rm K}(f)| = {\rm e}^{- {\rm a}_{\rm K}(f)}\hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm K}(f)\hspace{0.15cm}{\rm in }\hspace{0.15cm}{\rm Np}\hspace{0.05cm}.$$

Beachten Sie, dass das Dämpfungsmaß mit „alpha” bezeichnet wird und die Dämpfungsfunktion (nach Multiplikation mit der Länge) mit „a” , was beim verwendeten Zeichensatz schwer zu erkennen ist.

Die charakteristische Kabeldämpfung $a_∗$ eignet sich insbesondere für den Vergleich verschiedener leitungsgebundener Übertragungssysteme mit unterschiedlichen Bitraten $(R)$, Kabeltypen (zum Beispiel Normal– oder Kleinkoaxialkabel) und Kabellängen $l$. Bei all diesen Übertragungssystemen beschreibt $a_∗$ die Dämpfung bei der halben Bitrate unter Vernachlässigung des $α_0$ – und des $α_1$ –Terms: $${\rm a}_{\rm \star} = {\rm a}_{\rm K}(f = {R}/{2}) = \alpha_2 \cdot \sqrt {{R}/{2}} \cdot l\hspace{0.05cm}.$$ Die Beschreibung des rechten Diagramms folgt anschließend.

Charakteristische Kabeldämpfung (2)

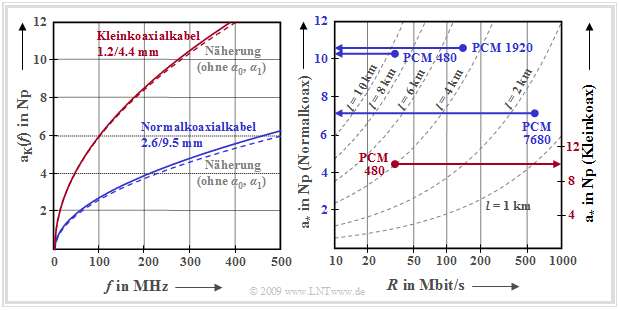
Das rechte Diagramm zeigt die charakteristische Kabeldämpfung $a_∗$ in Neper (Np) in Abhängigkeit der Bitrate $R$ und der Kabellänge $l$

beim Normalkoaxialkabel (linke Ordinatenbeschriftung) und
beim Kleinkoaxialkabel (rechte Ordinatenbeschriftung).

In der Grafik eingezeichnet sind die vom CCITT in den 1970–Jahren vorgeschlagenen PCM–Systeme der Hierarchiestufen 3 bis 5. Man erkennt:

Bei all diesen Systemen zur PCM–Sprachübertragung nimmt die charakteristische Kabeldämpfung Werte zwischen 7 Np (≈ 61 dB) und 10.6 Np (≈ 92 dB) an.
Das System PCM 480 – ausgelegt für 480 gleichzeitige Telefonate – mit der Bitrate $R$ ≈ 35 Mbit/s wurde sowohl für das Normalkoaxialkabel (mit der Leitungslänge $l =$ 9.3 km) als auch für das Kleinkoaxialkabel (mit 4 km Länge) spezifiziert. Die $a_∗$–Werte 10.4 Np bzw. 9.9 Np liegen in der gleichen Größenordnung.
Das Übertragungssystem PCM 1920 der vierten Hierarchiestufe $(R$ ≈ 140 Mbit/s, $l =$ 4.65 km, Normalkoaxialkabel) wird durch $a_∗$ = 10.6 Np bzw. 10.6 · 8.688 dB/Np ≈ 92 dB parametrisiert.
Obwohl das System PCM 7680 demgegenüber zwar die vierfache Kapazität $(R$ ≈ 560 Mbit/s) aufweist, ist die charakteristische Kabeldämpfung mit $a_∗$ ≈ 61 dB aufgrund der um den Faktor 3 kürzeren Kabelabschnitte $(l$ = 1.55 km, Normalkoaxialkabel) deutlich geringer.
Aus diesen Zahlenwerten geht auch hervor, dass bei Koaxialkabelsystemen die Kabellänge $l$ kritischer ist als die Bitrate $R$. Will man die Kabellänge verdoppeln, muss man die Bitrate um den Faktor 4 herabsetzen.

Die hier beschriebene Thematik können Sie sich auch mit folgendem Interaktionsmodul verdeutlichen: $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=2133&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=7761LSYGTN1463149483}{Dämpfung von Kupferkabeln}$

Impulsantworten von Koaxialkabeln (1)

Zur Berechnung der Impulsantwort können von den fünf Anteilen des Übertragungsmaßes die beiden ersten Dämpfungsanteile vernachlässigt werden (Begründung siehe vorheriger Abschnitt): $$\begin{align*}\gamma(f) & = \alpha_0 + \alpha_1 \cdot f + {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \approx \\ & \approx & {\rm j} \cdot \beta_1 \cdot f +\alpha_2 \cdot \sqrt {f}+ {\rm j}\cdot \beta_2 \cdot \sqrt {f} \hspace{0.05cm}.\end{align*}$$

Unter Berücksichtigung

der Kabellänge $l$,
der charakteristischen Kabeldämpfung $a_∗$ und
der Tatsache, dass $α_2$ (in Np) und $β_2$ (in rad) zahlenmäßig gleich sind,

gilt somit für den Frequenzgang des Koaxialkabels: $$\begin{align*}H_{\rm K}(f) & = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.05cm} \sqrt{2f/R} }\cdot {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}{\rm a}_{\rm \star}\hspace{0.05cm}\cdot \hspace{0.02cm} \sqrt{2f/R}}=\\ & = {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f} \cdot {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R}} \hspace{0.05cm},\end{align*}$$ $${\rm wobei} \hspace{0.15cm}b_1\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm rad)}= \beta_1 \cdot l \hspace{0.05cm}, \hspace{0.2cm} {\rm a}_{\rm \star}\hspace{0.1cm}{(\rm in }\hspace{0.15cm}{\rm Np)}= \alpha_2 \cdot \sqrt {R/2} \cdot l \hspace{0.05cm}.$$

Zur Zeitbereichsdarstellung kommt man durch Anwendung der $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=600&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=7761LSYGTN1463149483}{Fourierrücktransformation}$ und des Faltungssatzes: $$h_{\rm K}(t) = {\rm F}^{-1} \left \{ {\rm e}^{-{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm} b_1 f}\right \} \star {\rm F}^{-1} \left \{ {\rm e}^{-2{\rm a}_{\rm \star}\hspace{0.03cm}\cdot \hspace{0.03cm} \sqrt{ {\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}f/R} }\right \} \hspace{0.05cm}.$$

Hierbei ist zu berücksichtigen:

Der erste Term liefert die um die Phasenlaufzeit $τ_{\rm P} = b_1/2π$ verschobene Diracfunktion $δ(t – τ_{\rm P})$.
Der zweite Term lässt sich analytisch geschlossen angeben. Wir schreiben hierfür $h_{\rm K}(t + τ_P)$. Im Gegensatz zu $h_{\rm K}(t)$ ist hier die Phasenlaufzeit $τ_{\rm P}$ nicht berücksichtigt.

$$h_{\rm K}(t + \tau_{\rm P}) = \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \hspace{0.05cm}R \hspace{0.05cm}t^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \hspace{0.05cm}R\hspace{0.05cm} t}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$

Da die Bitrate $R$ bereits bei der Definition der charakteristischen Kabeldämpfung $a_∗$ berücksichtigt wurde, lässt sich diese Gleichung mit der normierten Zeit $t' = t/T$ einfach darstellen, wobei $T = 1/R$ die Symboldauer eines Binärsystems angibt. Desweiteren gilt $τ_{\rm P'} = τ_{\rm P}/T:$

$$h_{\rm K}(t' + \tau_{\rm P} ') = \frac {1}{T} \cdot \frac {{\rm a}_{\rm \star}}{\pi \cdot \sqrt{2 \hspace{0.05cm}t'^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \hspace{0.05cm}t'}} \right ]\hspace{0.05cm},\hspace{0.2cm}{\rm a}_{\rm \star}\hspace{0.15cm}{\rm in\hspace{0.15cm} Np}\hspace{0.05cm}.$$

Impulsantworten von Koaxialkabeln (2)

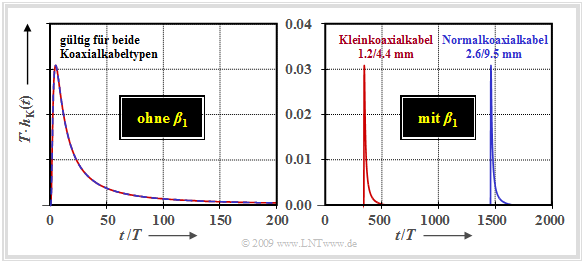
Dargestellt wird die normierte Impulsantwort $T · h_{\rm K}(t)$ eines Koaxialkabels mit $a_∗ =$ 60 dB (6.9 Np) $⇒ α_0$ und $α_1$ werden hier vernachlässigt. Für die linke Grafik wurde zudem der Parameter $β_1$ zu 0 gesetzt.

Wegen der Parametrisierung mittels der charakteristischen Kabeldämpfung $a_∗$ und der Normierung der Zeit auf die Symboldauer $T$ gilt diese linke Kurve für Systeme mit Klein– bzw. Normalkoaxialkabel, für unterschiedliche Längen und verschiedene Bitraten gleichermaßen, zum Beispiel für ein

Normalkoaxialkabel 2.6/9.5 mm, Bitrate $R =$ 140 Mbit/s, Kabellänge $l =$ 3 km ⇒ System A,
Kleinkoaxialkabel 1.2/4.4 mm, Bitrate $R =$ 35 Mbit/s, Kabellänge $l =$ 2.8 km ⇒ System B.

Man erkennt, dass sich selbst bei dieser moderaten Kabeldämpfung $a_∗ =$ 60 dB die Impulsantwort aufgrund des Skineffektes $(α_2 = β_2 ≠$ 0) schon über mehr als 200 Symboldauern erstreckt. Da das Integral über $h_{\rm K}(t)$ gleich $H_{\rm K}(f = 0) =$ 1 ist, wird der Maximalwert von $h_{\rm K}(t)$ sehr klein (≈ 0.03).

In der rechten Grafik sind die Auswirkungen des Phasenparameters $β_1$ zu sehen. Beachten Sie bitte auch die unterschiedlichen Zeitmaßstäbe in der linken und der rechten Darstellung:

Beim System A $(β_1 =$ 21.78 rad/(km · MHz), $T =$ 7.14 ns) führt $β_1$ zu einer Laufzeit von

$$\tau_{\rm A}= \frac {\beta_1 \cdot l}{2\pi} =\frac {21.78\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 3\,{\rm km} }{2\pi} = 10.4\,{\rm \mu s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm A}' = {\tau_{\rm A}}/{T} \approx 1457\hspace{0.05cm}.$$

Dagegen erhält man für das System B $(β_1 =$ 22.18 rad/(km · MHz), $T =$ 30 ns):

$$\tau_{\rm B}= \frac {\beta_1 \cdot l}{2\pi} =\frac {22.18\, { {\rm rad} }/{ {(\rm km \cdot MHz)} }\cdot 2.8\,{\rm km} }{2\pi} = 9.9\,{\rm \mu s}\hspace{0.3cm}\Rightarrow \hspace{0.3cm}\tau_{\rm B}' ={\tau_{\rm B}}/{T} \approx 330\hspace{0.05cm}.$$

Obwohl bei den getroffenen Annahmen $τ_A ≈ τ_B$ gilt, ergeben sich wegen der Zeitnormierung auf $T = 1/R$ völlig unterschiedliche Verhältnisse.

Bei der Simulation und Optimierung von Nachrichtensystemen verzichtet man meist auf den Phasenterm mit $b_1 = β_1 · l$, da dieser ausschließlich eine Laufzeit, aber keine Signalverzerrung zur Folge hat.

Empfangsgrundimpuls

Mit dem Sendegrundimpuls $g_s(t)$ und der Impulsantwort $h_{\rm K}(t)$ ergibt sich für den Empfangsgrundimpuls: $$g_r(t) = g_s(t) \star h_{\rm K}(t)\hspace{0.05cm}.$$ Verwendet man am Sender einen NRZ–Rechteckimpuls $g_s(t)$ mit der Amplitude $s_0$ und Dauer $Δt_s = T$, so ergibt sich für den Grundimpuls am Ausgang des Koaxialkabels: $$g_r(t) = 2 s_0 \cdot \left [ {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T - 0.5)}}\right ) - {\rm Q} \left (\frac {{\rm a}_{\rm \star}/\sqrt {\pi}}{ \sqrt{ (t/T + 0.5)}}\right ) \right ]\hspace{0.05cm},$$ mit $a_∗$: charakteristische Kabeldämpfung in Neper, $Q(x)$: komplemantäre Gaußsche Fehlerfunktion.

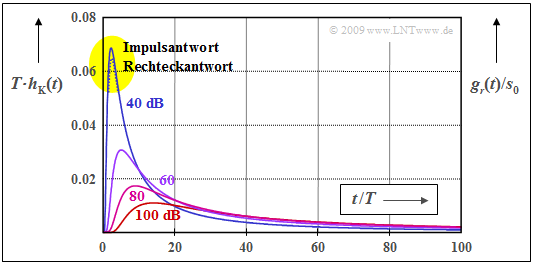
Die Abbildung zeigt die normierte Koaxialkabelimpulsantwort $T · h_{\rm K}(t)$ und den auf die Sendeamplitude $s_0$ normierten Empfangsgrundimpuls $g_r(t)$ für die charakteristischen Kabeldämpfungen $a_∗ =$ 40 dB, 60 dB, 80 dB und 100 dB. Kleinere Werte von $a_∗$ sind für die Praxis nicht relevant.

Man erkennt aus dieser Darstellung:

Mit $a_∗ =$ 40 dB ist $g_r(t)/s_0$ an der Spitze geringfügig (etwa um den Faktor 0.95) kleiner als die normierte Impulsantwort $T · h_{\rm K}(t)$.
Dagegen sind für den Fall $a_∗ ≥$ 60 dB die Rechteckantwort und die Impulsantwort innerhalb der Zeichengenauigkeit nicht zu unterscheiden.
Bei einem RZ–Impuls ist die obige Gleichung für den Empfangsgrundimpuls noch mit dem Tastverhältnis $Δts/T$ zu multiplizieren. In diesem Fall ist $g_r(t)/s_0$ deutlich kleiner als $T · h_{\rm K}(t)$.
Die so modifizierte Gleichung stellt auch eine gute Näherung für andere Sendegrundimpulse dar, so lange $a_∗$ hinreichend groß ist (≥ 60 dB). $Δt_s$ gibt dann die äquivalente Sendeimpulsdauer an.

Wir möchten Sie auf ein Interaktionsmodul hinweisen, das die hier behandelte Thematik zum Inhalt hat: $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=2430&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=7761LSYGTN1463149483}{Zeitverhalten von Kupferkabeln}$

Einige Bemerkungen zu Koaxialkabelsystemen

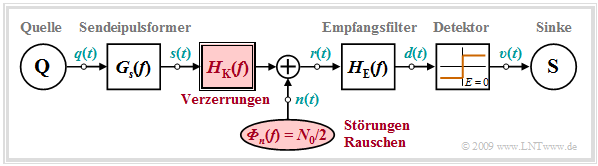
Geht man von binärer Übertragung mit NRZ–Rechteckimpulsen (Symboldauer $T$) und einem koaxialen Übertragungskanal aus, so ergibt sich das folgende Systemmodell:

Insbesondere ist zu beachten:

Bei einer Simulation lässt man zweckmäßigerweise die Laufzeit des Koaxialkabels außer Betracht. Dann gilt für den Empfangsgrundimpuls näherungsweise:

$$g_r(t) \approx s_0 \cdot T \cdot h_{\rm K}(t) = \frac {s_0 \cdot {\rm a}_{\rm \star}/\pi}{ \sqrt{2 \hspace{0.05cm}(t/T)^3}}\cdot {\rm exp} \left [ -\frac {{\rm a}_{\rm \star}^2}{ {2\pi \hspace{0.05cm}t/T}} \right ] \hspace{0.05cm}, \hspace{0.2cm} \hspace{0.15cm} {\rm mit}\hspace{0.15cm}{\rm a}_{\rm \star}\hspace{0.15cm} {\rm in}\hspace{0.15cm} {\rm Neper}\hspace{0.05cm}.$$

Das $\href{http://en.lntwww.de/cgi-bin/extern/uni.pl?uno=hyperlink&due=block&b_id=1231&hyperlink_typ=block_verweis&hyperlink_fenstergroesse=blockverweis_gross&session_id=7761LSYGTN1463149483}{thermische Rauschen}$ ist wegen der sehr guten Abschirmung der Koaxialkabel gegenüber anderen Störungen die dominante Störursache. $n(t)$ ist gaußverteilt und weiß und wird durch die (zweiseitige) Rauschleistungsdichte $N_0/2$ beschrieben.
Der weitaus größte Rauschanteil entsteht in der Eingangsstufe des Empfängers, so dass man $n(t)$ zweckmäßigerweise an der Schnittstelle Kabel–Empfänger addiert:

$$r(t) = \sum_{\nu = - \infty}^{+ \infty}a_{\nu}\cdot g_r(t - \nu \cdot T)+ n(t) \hspace{0.05cm} .$$

Dieser Punkt ist auch deshalb sinnvoll, da alle entlang des Kabels akkumulierten Rauschstörungen durch den Kabelfrequenzgang $H_{\rm K}(f)$ entscheidend gedämpft werden.