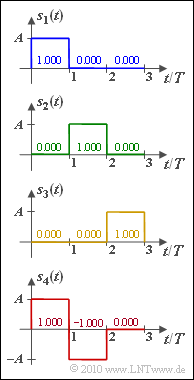
Exercise 4.1Z: Other Basis Functions

• Return to book

Energy-limited signals

This exercise pursues exactly the same goal as  "Exercise 4.1":

For  $M = 4$  energy-limited signals  $s_i(t)$  with  $i = 1, \ \text{...} \ , 4$,  the  $N$  required orthonormal basis functions  $\varphi_{\it j}(t)$  are to be found,  which must satisfy the following condition:

$$< \hspace{-0.1cm} \varphi_j(t), \hspace{0.1cm}\varphi_k(t) \hspace{-0.1cm} > \hspace{0.1cm} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \int_{-\infty}^{+\infty}\varphi_j(t) \cdot \varphi_k(t)\, {\rm d} t = {\rm \delta}_{jk} = \left\{ \begin{array}{c} 1 \\ 0 \end{array} \right.\quad \begin{array}{*{1}c} j = k \\ j \ne k \\ \end{array} \hspace{0.05cm}.$$

With  $M$  transmitted signals  $s_i(t)$,  already fewer basis functions  $\varphi_{\it j}(t)$  can suffice,  namely  $N$.  Thus,  in general,  $N ≤ M$.

These are exactly the same energy-limited signals  $s_i(t)$  as in  "Exercise 4.1":

• The difference is the different order of the signals  $s_i(t)$.

• In this exercise,  these are sorted in such a way that the basis functions can be found without using the more cumbersome  "Gram-Schmidt process". 

Notes:

• The exercise belongs to the chapter  "Signals, Basis Functions and Vector Spaces".

• For numerical calculations,  use:   $A = 1 \sqrt{\rm W} , \hspace{0.2cm} T = 1\,{\rm µ s} \hspace{0.05cm}.$

Questions

1

In Exercise 4.1,  the Gram-Schmidt process resulted in  $N = 3$  basis functions.  How many basis functions are needed here?

$N \ = \ $

2

Give the 2–norm of all these signals:

$||s_1(t)|| \ = \ $ $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$

$||s_2(t)|| \ = \ $ $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$

$||s_3(t)|| \ = \ $ $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$

$||s_4(t)|| \ = \ $ $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$

3

Which statements are true for the basis functions  $\varphi_1(t)$,  $\varphi_2(t)$  and  $\varphi_3(t)$?

	The basis functions computed in  "Exericse 4.1"  are also appropriate here.
	There are infinitely many possibilities for  $\{\varphi_1(t),\ \varphi_2(t),\ \varphi_3(t)\}$.
	A possible set is  $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)\}$,  with  $j = 1,\ 2,\ 3$.
	A possible set is  $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$,  with  $j = 1,\ 2,\ 3$.

4

What are the coefficients of the signal  $s_4(t)$  with respect to the basis functions  $\{\varphi_{\it j}(t)\} = \{s_{\it j}(t)/K\}$, with  $j = 1,\ 2,\ 3$?

$s_{\rm 41} \ = \ $ $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$

$s_{\rm 42} \ = \ $ $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$

$s_{\rm 43} \ = \ $ $\ \cdot \ 10^{\rm –3} \ \rm \sqrt{Ws}$

Solution

Solution

(1)  The only difference to Exercise 4.1 is the different numbering of the signals $s_i(t)$.

• Thus it is obvious that $\underline {N = 3}$ must hold here as well.

(2)  The 2–norm gives the root of the signal energy and is comparable to the rms value for power-limited signals.

• The first three signals all have the 2–norm

$$||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = \sqrt{A^2 \cdot T}\hspace{0.1cm}\hspace{0.15cm}\underline { = 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$

• The norm of the last signal is larger by a factor of $\sqrt{2}$:

$$||s_4(t)|| \hspace{0.1cm}\hspace{0.15cm}\underline { = 1.414 \cdot 10^{-3}\sqrt{\rm Ws}} \hspace{0.05cm}.$$

Basisfunktionssatz (3)  The first and last statements are true in contrast to statements 2 and 3:

• It would be completely illogical if the basis functions found should no longer hold when the signals $s_i(t)$ are sorted differently.
• The Gram–Schmidt process yields only one possible set $\{\varphi_{\it j}(t)\}$ of basis functions. A different sorting (possibly) yields a different one.
• The number of permutations of  $M = 4$  signals is  $4! = 24$. In any case, there cannot be more basis function sets   ⇒   solution 2 is wrong.
• However, there are probably (because of $N = 3$) only $3! = 6$ possible sets of basis functions. As can be seen from the sample "solution" to Exercise 4.1, the same basis functions will result with the order $s_1(t), s_2(t), s_4(t), s_3(t)$ as with $s_1(t), s_2(t), s_3(t), s_4(t)$. However, this is only a conjecture of the authors; we have not checked it.
• Statement 3 cannot be true simply because of the different units of $s_i(t)$ and $\varphi_{\it j}(t)$. Like $A$, the signals have the unit $\sqrt{\rm W}$, the basis functions the unit $\sqrt{\rm 1/s}$.
• Thus, the last solution is correct, where for $K$ holds:

$$K = ||s_1(t)|| = ||s_2(t)|| = ||s_3(t)|| = 10^{-3}\sqrt{\rm Ws} \hspace{0.05cm}.$$

Ende Basisfunktionssatz

(4)  From the comparison of the diagrams in the specification section we can see:

$$s_{4}(t) = s_{1}(t) - s_{2}(t) = K \cdot \varphi_1(t) - K \cdot \varphi_2(t)\hspace{0.05cm}.$$

• Furthermore holds:

$$s_{4}(t) = s_{41}\cdot \varphi_1(t) + s_{42}\cdot \varphi_2(t) + s_{43}\cdot \varphi_3(t)$$

$$\Rightarrow \hspace{0.3cm}s_{41} = K \hspace{0.1cm}\hspace{0.15cm}\underline {= 10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{42} = -K \hspace{0.1cm}\hspace{0.15cm}\underline {= -10^{-3}\sqrt{\rm Ws}}\hspace{0.05cm}, \hspace{0.2cm}s_{43} \hspace{0.1cm}\hspace{0.15cm}\underline { = 0}\hspace{0.05cm}.$$