Exercise 1.16: Block Error Probability Bounds for AWGN

Function ${\rm Q}(x)$ and approximations;
it holds: ${\rm Q_u}(x)\le{\rm Q}(x)\le{\rm Q_o}(x)$

We assume the following constellation:

A linear block code with code rate $R = k/n$ and distance spectrum $\{W_i\}, \ i = 1, \ \text{...} \ , n$,

an AWGN channel characterized by $E_{\rm B}/N_{0}$ ⇒ convertible to noise power $\sigma^2$,

a receiver based on "soft decision" as well as the "maximum likelihood criterion".

Under the assumption valid for the entire exercise that always the zero-word $\underline{x}_{1} = (0, 0, \text{... } \ , 0)$ is sent, the "pairwise error probability" with a different code word $\underline{x}_{l} (l = 2,\ \text{...} \ , 2^k)$:

$$ {\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = {\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm}.$$

The derivation of this relation can be found in [Liv10]. Used in this equation are:

the "complementary Gaussian error function" ${\rm Q}(x)$,

the "Hamming weight" $w_{\rm H}(\underline{x}_{l})$ of the code word $\underline{x}_{l}$,

the "AWGN noise power" $\sigma^2 = (2 \cdot R \cdot E_{\rm B}/N_{0})^{-1}.$

This allows various bounds to be specified for the block error probability:

the so called "Union Bound" $\rm (UB)$:

$$p_1 = \sum_{l = 2}^{2^k}\hspace{0.05cm}{\rm Pr}[\hspace{0.05cm}\underline{x}_{\hspace{0.02cm}1} \hspace{-0.02cm}\mapsto \hspace{-0.02cm}\underline{x}_{\hspace{0.02cm}l}\hspace{0.05cm}] = \sum_{l \hspace{0.05cm}= \hspace{0.05cm}2}^{2^k}\hspace{0.05cm}{\rm Q}\left ( \sqrt{w_{\rm H}(\underline{x}_{\hspace{0.02cm}l})/\sigma^2} \right ) \hspace{0.05cm},$$

the so called "Truncated Union Bound" $\rm (TUB)$:

$$p_2 = W_{d_{\rm min}} \cdot {\rm Q}\left ( \sqrt{d_{\rm min}/\sigma^2} \right ) \hspace{0.05cm},$$

the "Bhattacharyya Bound":

$$p_3 = W(\beta) - 1\hspace{0.05cm},\hspace{0.2cm} {\rm with}\hspace{0.15cm} \beta = {\rm e}^{ - 1/(2\sigma^2) } \hspace{0.05cm}.$$

In this case, replace the distance spectrum $\{W_i\}$ with the weight enumerator function:

$$\left \{ \hspace{0.05cm} W_i \hspace{0.05cm} \right \} \hspace{0.3cm} \Leftrightarrow \hspace{0.3cm} W(X) = \sum_{i=0 }^{n} W_i \cdot X^{i} = W_0 + W_1 \cdot X + W_2 \cdot X^{2} + ... \hspace{0.05cm} + W_n \cdot X^{n}\hspace{0.05cm}.$$

In the transition from the "Union Bound" $p_{1}$ to the more imprecise bound $p_{3}$ among others

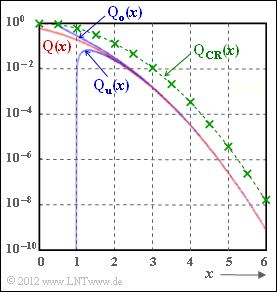
the function ${\rm Q}(x)$ is replaced by the "Chernoff-Rubin bound" ${\rm Q}_{\rm CR}(x)$.

Both functions are shown in the above graph (red and green curve, resp.).

In the "Exercise 1.16Z" the relationship between these functions is evaluated numerically and referenced to the bounds ${\rm Q}_{\rm o}(x)$ and ${\rm Q}_{\rm u}(x)$ which are also drawn in the above graph.

Hints:

This exercise belongs to the chapter "Bounds for Block Error Probability".

The above cited reference "[Liv10]" refers to the lecture manuscript "Liva, G.: Channel Coding. Chair of Communications Engineering, TU Munich and DLR Oberpfaffenhofen, 2010."

Further we refer to the interactive applet "Complementary Gaussian error functions".

Questions

	$p_{1} = \sum_{l\hspace{0.05cm}=\hspace{0.05cm}2}^{2^k} W_{l} · {\rm Q}\big[(l/\sigma^2)^{0.5}\big],$
	$p_{1} = \sum_{i\hspace{0.05cm}=\hspace{0.05cm}1}^{n} W_{i} · {\rm Q}\big[(i/\sigma^2)^{0.5}\big].$

$\sigma = 1.0 \text{:} \hspace{0.4cm} p_{1} \ = \ $

$\ \%$

$\sigma = 0.5 \text{:} \hspace{0.4cm} p_{1} \ = \ $

$\ \%$

$\sigma = 1.0 \text{:} \hspace{0.4cm} p_{2} \ = \ $

$\ \%$

$\sigma = 0.5 \text{:} \hspace{0.4cm} p_{2} \ = \ $

$\ \%$

	The block error probability is never greater than $p_{1}$.
	The block error probability is never greater than $p_{2}$.

	Replace the error function ${\rm Q}(x)$ with the function ${\rm Q}_{\rm CR}(x)$.
	Set the Bhattacharyya parameter $\beta = 1/\sigma$.
	Instead of $\{W_i\}$ uses the weight enumerator function $W(X)$.

$\sigma = 1.0 \text{:} \hspace{0.4cm} p_{3} \ = \ $

$\ \%$

$\sigma = 0.5 \text{:} \hspace{0.4cm} p_{3} \ = \ $

$\ \%$

Solution

(1) Richtig ist die Antwort 2. Das Distanzspektrum $\{W_i\}$ ist definiert für $i = 0, \ \text{...} \ , \ n$:

$W_{1}$ indicates how often the Hamming weight $w_{\rm H}(\underline{x}_{i}) = 1$ occurs.
$W_{n}$ indicates how often the Hamming weight $w_{\rm H}(\underline{x}_{i}) = n$ occurs.

With that, the Union Bound is:

$$p_1 = {\rm Pr(Union \hspace{0.15cm}Bound)}= \sum_{i = 1}^{n}\hspace{0.05cm}W_i \cdot {\rm Q}\left ( \sqrt{i/\sigma^2} \right ) \hspace{0.05cm}.$$

(2) The distance spectrum of the $(8, 4, 4)$ code was given as $W_{0} = 1 , \ W_{4} = 14, \ W_{8} = 1$. Thus, one obtains for $\sigma = 1$:

$$p_1 = W_4 \cdot {\rm Q}\left ( 2 \right ) + W_8 \cdot {\rm Q}\left ( 2 \cdot \sqrt{2} \right ) = 14 \cdot 2.28 \cdot 10^{-2}+ 1 \cdot 0.23 \cdot 10^{-2} \hspace{0.15cm}\underline{\approx 32.15\%}\hspace{0.05cm},$$

or for $\sigma = 0.5$:

$$p_1 = 14 \cdot {\rm Q}\left ( 4 \right ) + {\rm Q}\left ( 4 \cdot \sqrt{2} \right ) = 14 \cdot 3.17 \cdot 10^{-5}+ 1.1 \cdot 10^{-8} \hspace{0.15cm}\underline{\approx 0.0444 \%}\hspace{0.05cm}.$$

(3) With the minimum distance $d_{\rm min} = 4$ we get:

$$\sigma = 1.0\text{:} \hspace{0.4cm} p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} W_4 \cdot {\rm Q}\left ( 2 \right ) \hspace{0.15cm}\underline{= 31.92\%}\hspace{0.05cm},$$

$$\sigma = 0.5\text{:} \hspace{0.4cm} p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm}W_4 \cdot {\rm Q}\left ( 4 \right ) \approx p_1 \hspace{0.15cm}\underline{ = 0.0444 \%}\hspace{0.05cm}.$$

(4) The correct solution is suggestion 1:

The Union Bound - denoted here by $p_{1}$ - is an upper bound on the block error probability in all cases.
For the bound $p_{2}$ (Truncated Union Bound) this is not always true.
For example, in the $(7, 4, 3)$ Hamming code ⇒ $W_{3} = W_{4} = 7, \ W_{7} = 1$ is obtained with standard deviation $\sigma = 1$:

$$p_2 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} 7 \cdot {\rm Q}\left ( \sqrt{3} \right ) = 7 \cdot 4.18 \cdot 10^{-2} \approx 0.293\hspace{0.05cm},$$

$$p_1 \hspace{-0.15cm}\ = \ \hspace{-0.15cm} p_2 + 7 \cdot {\rm Q}\left ( \sqrt{4} \right )+ 1 \cdot {\rm Q}\left ( \sqrt{7} \right ) \approx 0.455 \hspace{0.05cm}.$$

The actual block error probability is likely to be between $p_{2} = 29.3\%$ and $p_{1} = 45.5\%$ (but has not been verified).
That is, $p_{2}$ is not an upper bound.

(5) Correct are suggested solutions 1 and 3, as the following calculation for the $(8, 4, 4)$ code shows:

It holds ${\rm Q}(x) ≤ {\rm Q_{CR}}(x) = {\rm e}^{-x^2/2}$. Thus, for the Union Bound

$$p_1 = W_4 \cdot {\rm Q}\left ( \sqrt{4/\sigma^2} \right ) +W_8 \cdot {\rm Q}\left ( \sqrt{8/\sigma^2} \right )$$

another upper bound can be specified:

$$p_1 \le W_4 \cdot {\rm e}^{ - {4}/(2 \sigma^2) } +W_8 \cdot {\rm e}^{ - {8}/(2 \sigma^2) } \hspace{0.05cm}.$$

With $\beta = {\rm e}^{-1/(2\sigma^2)}$ can be written for this also (so the given $\beta = 1/\sigma$ is wrong):

$$p_1 \le W_4 \cdot \beta^4 + W_8 \cdot \beta^8 \hspace{0.05cm}.$$

The weight function of the $(8, 4, 4)$ code is:

$$W(X) = 1 + W_4 \cdot X^4 + W_8 \cdot X^8 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} W(\beta) - 1 = W_4 \cdot \beta^4 + W_8 \cdot \beta^8\hspace{0.3cm} \Rightarrow \hspace{0.3cm} p_3 = W(\beta) - 1 \ge p_1\hspace{0.05cm}.$$

(6) With $\sigma = 1$, the Bhattacharyya parameter is $\beta = {\rm e}^{-0.5} = 0.6065$, and thus one obtains for the Bhattacharyya bound:

$$p_3 = 14 \cdot \beta^4 + \beta^8 = 14 \cdot 0.135 + 0.018= 1.913 \hspace{0.15cm}\underline{= 191.3%}\hspace{0.05cm}.$$

Considering that $p_{3}$ is a bound for a probability, $p_{3} = 1.913$ is only a trivial bound.
For $\sigma = 0.5$, on the other hand, $\beta = {\rm e}^{-2} \approx 0.135.$ Then holds:

$$p_3 = 14 \cdot \beta^4 + \beta^8 = 14 \cdot 3.35 \cdot 10^{-4} + 1.1 \cdot 10^{-7} \hspace{0.15cm}\underline{= 0.47 \%}\hspace{0.05cm}.$$

A comparison with subtask (2) shows that in the present example the Bhattacharyya bound $p_{3}$ is above the union bound $p_{1}$ by a factor $(0.47 - 10^{-2})/(0.044 - 10^{-2}) > 10$.

The reason for this large deviation is the Chernoff-Rubin bound, which is well above the ${\rm Q}$ function.
In "Exercise 1.16Z", the deviation between ${\rm Q}_{\rm CR}$ and ${\rm Q}(x)$ is also calculated quantitatively:

$${{\rm Q_{CR}}( x )}/{{\rm Q}( x )} \approx 2.5 \cdot x \hspace{0.3cm} \Rightarrow \hspace{0.3cm} {{\rm Q_{CR}}( x = 4 )}/{{\rm Q}( x = 4)} \approx 10 \hspace{0.05cm}.$$