Exercise 4.16: Binary Frequency Shift Keying
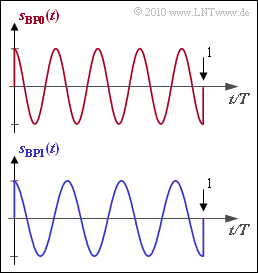
In binary FSK, the two messages $m_0$ and $m_1$ are represented by two different frequencies. For the two possible band–pass signals then applies in each case in the range $0 ≤ t ≤ T$ with $f_0 = f_{\rm T} + \Delta f_{\rm A}$ as well as $f_1 = f_{\rm T} \, – \Delta f_{\rm A}$:
- $$s_{\rm BP0}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{2E/T} \cdot \cos( 2\pi f_0 t)\hspace{0.05cm},$$
- $$ s_{\rm BP1}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{2E/T} \cdot \cos( 2\pi f_1 t)\hspace{0.05cm}.$$
The graph shows example signals $($in each case only one symbol duration $T)$.
- In obiger Gleichung gibt $f_{\rm T}$ die Trägerfrequenz an und $\Delta f_{\rm A}$ den Frequenzhub als die maximale Abweichung der Augenblicksfrequenz von der Trägerfrequenz an.
- $E$ ist die Signalenergie. Dabei gilt gleichermaßen für die mittlere Symbolenergie und die mittlere Bitenergie:
- $$E_{\rm S} = E_{\rm B} = E\hspace{0.05cm}.$$
Meist arbeitet man aber mit dem Modulationsindex, der als das Verhältnis von Gesamtfrequenzhub und Symbolrate definiert ist:
- $$h = \frac{2 \cdot \Delta f_{\rm A}}{1/T} = 2 \cdot \Delta f_{\rm A} \cdot T \hspace{0.05cm}.$$
Die äquivalente Tiefpassdarstellung führt unter Verwendung von $h$ zu den beiden komplexen Signalen
- $$ s_{\rm TP0}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}+{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm},$$
- $$ s_{\rm TP1}(t) \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \sqrt{E/T} \cdot {\rm e}^{\hspace{0.05cm}-{\rm j} \hspace{0.03cm}\cdot \hspace{0.03cm} \pi \hspace{0.03cm}\cdot \hspace{0.03cm} h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T}\hspace{0.05cm},\hspace{0.2cm} 0 \le t \le T\hspace{0.05cm}.$$
Eine orthogonale FSK liegt vor, wenn das innere Produkt den Wert $0$ ergibt:
- $$< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t =0 \hspace{0.05cm}.$$
In diesem Fall ist auch eine nichtkohärente Demodulation wie im Kapitel Trägerfrequenzensysteme mit nichtkohärenter Demodulation beschrieben möglich.
Das innere Produkt der Bandpass–Signale kann aus dem inneren Produkt der Tiefpass–Signale durch Realteilbildung ermittelt werden:
- $$< \hspace{-0.05cm}s_{\rm BP0}(t) \cdot s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \hspace{0.1cm}< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.15cm} \right ]\hspace{0.05cm}.$$
Gilt $〈 s_{\rm BP0}(t) \cdot s_{\rm BP1}(t)〉 = 0$, aber gleichzeitig auch $〈 s_{\rm TP0}(t) \cdot s_{\rm TP1}(t)〉 ≠ 0$,
- so ist eine kohärente Demodulation möglich,
- aber keine nichtkohärente Demodulation.
Hinweise:
- Die Aufgabe gehört zum Kapitel "Carrier Frequency Systems with Coherent Demodulation".
- Bezug genommen wird insbesondere auf die Seiten Binary Frequency Shift Keying (BFSK) und Minimum Shift Keying (MSK).
Fragebogen
Musterlösung
- Daraus berechnen sich Trägerfrequenzen und Frequenzhub zu
- $$f_{\rm T} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 + f_1) = \underline{4 \cdot 1/T}\hspace{0.05cm},$$
- $$ \Delta f_{\rm A} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} {1}/{2}\cdot (f_0 - f_1)= \underline{0.5 \cdot 1/T }\hspace{0.05cm}.$$
(2) Mit der angegebenen Gleichung gilt für den Modulationsindex:
- $$h = 2 \cdot \Delta f_{\rm A} \cdot T = 2 \cdot 0.5 \cdot 1/T \cdot T \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{h= 1}\hspace{0.05cm}. $$
(3) Das innere Produkt der Tiefpass–Signale lautet:
- $$< \hspace{-0.05cm} s_{\rm TP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm TP1}(t) \hspace{-0.05cm} > \hspace{0.2cm} = \int_{0}^{T} s_{\rm TP0}(t) \cdot s_{\rm TP1}^{\star}(t) \,{\rm d} t = \frac{E}{T} \cdot \int_{0}^{T} {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h \hspace{0.03cm}\cdot \hspace{0.03cm}t/T} \,{\rm d} t = \frac{E}{{\rm j}2\pi h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ] \hspace{0.05cm}.$$
Orthogonalität bedeutet, dass dieses innere Produkt $0$ sein muss:
- $$< \hspace{-0.05cm} s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm} > \hspace{0.2cm} = \frac{E}{{\rm j}2\pi h} \cdot \left [ {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ] = 0 \hspace{0.3cm}\Rightarrow \hspace{0.3cm} h = 1, 2, 3, ...$$
Richtig sind demzufolge die Lösungsvorschläge 3 und 4:
- Ist der Modulationsindex $h$ ganzzahlig, so kann nichtkohärent demoduliert werden, ohne dass die Orthogonalität verletzt wird.
(4) Richtig sind die Lösungsvorschläge 1, 3 und 4:
- Für das innere Produkt der Bandpass–Signale kann nach den Erläuterungen auf der Angabenseite geschrieben werden:
- $$< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \hspace{0.1cm}< \hspace{-0.05cm}s_{\rm TP0}(t) \cdot s_{\rm TP1}(t) \hspace{-0.05cm}> \hspace{0.2cm} \right ] = {\rm Re}\left [ \frac{E}{{\rm j}2\pi h} \cdot \left ( {\rm e}^{\hspace{0.05cm}{\rm j} 2\pi h} - 1 \right ) \right ]$$
- $$ \Rightarrow\hspace{0.3cm}< \hspace{-0.05cm}s_{\rm BP0}(t) \hspace{0.01cm} \ \cdot \ \hspace{0.01cm} s_{\rm BP1}(t) \hspace{-0.05cm}> \hspace{0.2cm}= {\rm Re}\left [ \frac{E}{2\pi h} \cdot \left ( \sin( 2\pi h) - {\rm j} \cdot [\cos( 2\pi h) - 1 ]\right ) \right ] = \frac{E \cdot \sin( 2\pi h)}{2\pi h} \hspace{0.05cm}.$$
- Dieses Ergebnis ist immer dann $0$, wenn der Modulationsindex $h$ ein ganzzahliges Vielfaches von $0.5$ ist.
(5) Richtig ist nur der Lösungsvorschlag 2.
- Für kohärente Demodulation muss $h$ ein Vielfaches von $0.5$ sein.
- Ist nichtkohärente Demodulation möglich, wie zum Beispiel im hier betrachteten Fall ($h = 1$), so ist auch kohärente Demodulation anwendbar.
- Dagegen kann für $h = 0.5$ zwar kohärent demoduliert werden, aber eine nichtkohärente Demodulation (die auf die Hüllkurve angewiesen ist) versagt.