Exercise 5.7Z: McCullough Model once more
As in "Exercise 5.6", "Exercise 5.6Z" and "Exercise 5.7", we consider the burst error channel model according to Gilbert and Elliott (GE model) with the parameters
- $$p_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.001, \hspace{0.2cm}p_{\rm B} = 0.1,\hspace{0.2cm} p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.1, \hspace{0.2cm} p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.01\hspace{0.05cm}.$$
From these four probabilities, the corresponding characteristics of the channel model according to McCullough (MC model) can be determined in such a way that both models have exactly the same statistical properties, namely
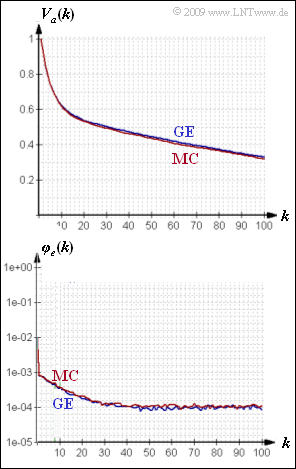
- exactly the same error distance distribution (EDD) $V_a(k)$,
- exactly the same error correlation function (ECF) $\varphi_e(k)$.
The probabilities of the MC model were determined in "Exercise 5.7" as follows $($labels according to the graph for Exercise 5.7, all with $q$ instead of $p)$:
- $$q_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.0061, \hspace{0.2cm}q_{\rm B} = 0.1949,\hspace{0.2cm} q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)\hspace{-0.1cm} \ = \ \hspace{-0.1cm} 0.5528, \hspace{0.2cm} q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G) = 0.3724\hspace{0.05cm}.$$
The upper graph shows the functions $V_a(k)$ and $\varphi_e(k)$ simulatively determined from $N = 10^6$ sequence elements for the GE and MC models. There are still slight discrepancies here. In the limiting case for $N → ∞$, on the other hand, error correlation function and error distance distribution of both models agree exactly.
In this exercise, important descriptive variables of the GE model such as
- state probabilities,
- mean error probabilities, and
- correlation duration
should be determined directly from the $q$ parameters of the MC model.
Notes:
- The exercise belongs to the chapter "Burst Error Channels".
- From the above exercises, the following results can be further used:
- (a) The state probabilities of the GE model are
- $$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} \hspace{0.05cm},\hspace{0.2cm} w_{\rm B} = 1 - w_{\rm G }\hspace{0.05cm}.$$
- (b) The mean error probability of the GE model is
- $$p_{\rm M} = w_{\rm G} \cdot p_{\rm G} + w_{\rm B} \cdot p_{\rm B} = \varphi_{e}(k = 0 )\hspace{0.05cm}.$$
- (c) The correlation duration of the GE model is calculated as
- $$D_{\rm K} =\frac{1}{{\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )}-1 \hspace{0.05cm}.$$
Questions
Musterlösung
- $$w_{\rm G} = \frac{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{p(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + p(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)} = 0.909 \hspace{0.05cm},\hspace{0.5cm} w_{\rm B} = 1 - w_{\rm G }= 0.091\hspace{0.05cm}.$$
- Dagegen erhält man beim MC–Modell:
- $$\alpha_{\rm G} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} \frac{q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B)}{q(\rm G\hspace{0.05cm}|\hspace{0.05cm} B) + q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G)}= \frac{0.5528}{0.5528 + 0.3724}\hspace{0.15cm}\underline {= 0.5975}\hspace{0.05cm},\hspace{0.5cm} \alpha_{\rm B} \hspace{-0.1cm} \ = \ \hspace{-0.1cm} 1 - \alpha_{\rm G} \hspace{0.15cm}\underline {= 0.4025}\hspace{0.05cm}.$$
- In der Teilaufgabe (3) der Aufgabe 5.7 wurden diese Werte schon einmal ermittelt, allerdings aus den Parametern des äquivalenten Gilbert–Elliott–Modells.
(2) Der mittlere Fehlerabstand im Kanalzustand "GOOD" ist gleich dem Kehrwert der dazugehörigen Fehlerwahrscheinlichkeit $q_{\rm G}$.
- Der mittlere Fehlerabstand im Zustand "BAD" ist dementsprechend $1/q_{\rm B}$.
- Durch Gewichtung mit den beiden Zustandswahrscheinlichkeiten $\alpha_{\rm G}$ und $\alpha_{\rm B}$ ergibt sich der mittlere Fehlerabstand des MC–Modells insgesamt zu
- $${\rm E}[a] =\frac{\alpha_{\rm G}}{q_{\rm G}} + \frac{\alpha_{\rm B}}{q_{\rm B}}=\frac{0.5975}{0.0061} + \frac{0.4025}{0.1949} = 97.95 + 2.06\hspace{0.15cm}\underline { = 100.1}\hspace{0.05cm}.$$
- Dieser Wert sollte natürlich genau so groß wie beim entsprechenden GE–Modell sein.
- Die kleine Abweichung von $0.1$ ist auf Rundungsfehler zurückzuführen.
(3) Auch hier gilt der Zusammenhang $\varphi_e(k = 0) = p_{\rm M}$.
- Die mittlere Fehlerwahrscheinlichkeit ist aber gleich dem Kehrwert des mittleren Fehlerabstands ${\rm E}[a]$.
- Daraus folgt $\varphi_e(k = 0) \ \underline {= 0.01}$.
(4) Beim GE–Modell ist die Korrelationsdauer wie folgt gegeben ($S$ steht für Summe):
- $$D_{\rm K} = {1}/{S}-1 \hspace{0.05cm},\hspace{0.2cm}S = {\rm Pr}(\rm G\hspace{0.05cm}|\hspace{0.05cm} B ) + {\rm Pr}(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )\hspace{0.05cm}.$$
- Weiter gilt mit den Angaben zur Aufgabe 5.7:
- $$q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) = \frac{\alpha_{\rm B} \cdot S}{\alpha_{\rm G} \cdot q_{\rm B} + \alpha_{\rm B} \cdot q_{\rm G}} \hspace{0.05cm}, \hspace{0.2cm}q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })= \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G )$$
- $$\Rightarrow \hspace{0.3cm} S = q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G }) + q_{\rm B} \cdot \frac{\alpha_{\rm G}}{\alpha_{\rm B}} \cdot q(\rm B\hspace{0.05cm}|\hspace{0.05cm} G ) = q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G })+ q_{\rm B} \cdot q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B }) \hspace{0.05cm}.$$
- $$\Rightarrow \hspace{0.3cm}D_{\rm K} =\frac{1}{q_{\rm G} \cdot q({\rm B\hspace{0.05cm}|\hspace{0.05cm} G })+ q_{\rm B} \cdot q({\rm G\hspace{0.05cm}|\hspace{0.05cm} B })}-1 \hspace{0.05cm}.$$
- Richtig ist also der Lösungsvorschlag 2. Mit den gegebenen Parameterwerten erhält man zum Beispiel:
- $$D_{\rm K} =\frac{1}{0.0061 \cdot 0.3724 + 0.1949 \cdot 0.5528}-1=\frac{1}{0.11}-1 {\approx 8.09}\hspace{0.05cm}.$$
- Es ergibt sich exakt der gleiche Wert wie in der Teilaufgabe (3) von Aufgabe 5.6.