Exercise 2.6: GF(P power m). Which P, which m?

Underlying tables for
addition and multiplication

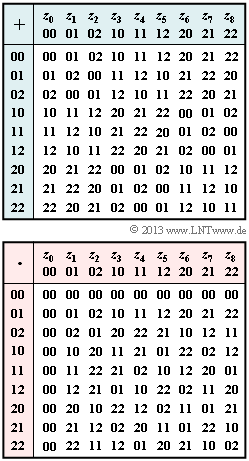
A Galois field ${\rm GF}(q)$ with $q = P^m$ elements defined by the adjacent tables is to be analyzed

for addition $($marked with "$+$"$)$, and

for multiplication $($marked with "$\hspace{0.05cm}\cdot\hspace{0.05cm}$)".

This Galois field ${\rm GF}(q) = \{\hspace{0.1cm}z_0,\hspace{0.1cm} z_1,\hspace{0.05cm} \text{...} , \hspace{0.1cm}z_{q-1}\}$ satisfies all the requirements for a finite field listed in the chapter "Some Basics of Algebra" . Thus, commutative, associative and distributive laws are also satisfied.

Furthermore there is

a neutral element with respect to addition ⇒ $N_{\rm A}$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i + z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm A} \hspace{0.25cm}{\rm (zero\hspace{0.15cm}element)} \hspace{0.05cm},$$

a neutral element with respect to multiplication ⇒ $N_{\rm M}$:

$$\exists \hspace{0.15cm} z_j \in {\rm GF}(q)\text{:} \hspace{0.25cm}z_i \cdot z_j = z_i \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_j = N_{\rm M} \hspace{0.25cm}{\rm (identity\hspace{0.15cm}element)} \hspace{0.05cm},$$

for all elements $z_i$ an additive inverse ⇒ ${\rm Inv_A}(z_i)$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q)\hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_A}(z_i) \in {\rm GF}(q)\text{:}$$

$$z_i + {\rm Inv_A}(z_i) = N_{\rm A} = {\rm "\hspace{-0.15cm}0\hspace{-0.1cm}"}\hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm short}\text{:}\hspace{0.15cm} {\rm Inv_A}(z_i) = - z_i \hspace{0.05cm}, $$

for all elements $z_i$ except the zero element a multiplicative inverse ⇒ ${\rm Inv_M}(z_i)$:

$$\forall \hspace{0.15cm} z_i \in {\rm GF}(q),\hspace{0.15cm} z_i \ne N_{\rm A} \hspace{0.15cm} \exists \hspace{0.15cm} {\rm Inv_M}(z_i) \in {\rm GF}(q)\text{:}$$

$$z_i \cdot {\rm Inv_M}(z_i) = N_{\rm M} = {\rm "\hspace{-0.15cm}1\hspace{-0.1cm}"} \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm short}\text{:}\hspace{0.15cm} {\rm Inv_M}(z_i) = z_i^{-1} \hspace{0.05cm}. $$

Hints:

This exercise belongs to the chapter "Extension Field".

In the tables, the elements $z_0, \hspace{0.05cm} \text{...} \hspace{0.1cm} , \ z_8$ are called "coefficient vectors".

For example, "$2 \hspace{0.03cm}1$" stands for "$2 \cdot \alpha + 1$".

Questions

Solution

(1) Each element consists of two ternaries ⇒ $\underline{P = 3}, \ \underline{m = 2}$. There are $q = P^m = 3^8 = \underline{9 \rm \hspace{0.2cm}elements}$.

(2) Correct is the proposed solution 1:

The neutral element of the addition $(N_{\rm A})$ satisfies for all $z_i ∈ {\rm GF}(P^m)$ the condition $z_i + N_{\rm A} = z_i$.
From the addition table it can be read that "$0\hspace{0.03cm}0$" satisfies this condition.

(3) Correct is the proposed solution 2:

The neutral element of the multiplication $(N_{\rm M})$ must always satisfy the condition $z_i \cdot N_{\rm M} = z_i$.

From the multiplication table, $N_{\rm M} = \, "\hspace{-0.15cm}0\hspace{0.03cm}1\hspace{-0.1cm}"$.

In polynomial notation, this corresponds to $k_1 = 0$ and $k_0 = 1$:

$$k_1 \cdot \alpha + k_0 = 1 \hspace{0.05cm}.$$

(4) With the polynomial representation, the following calculations result:

$${\rm Inv_A}("\hspace{-0.05cm}0\hspace{0.03cm}2") \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(2) = (-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = 1 \hspace{0.25cm}\Rightarrow \hspace{0.25cm}{\rm vector}\hspace{0.15cm}"\hspace{-0.1cm}0\hspace{0.03cm}1\hspace{-0.1cm}"\hspace{0.05cm},$$

$${\rm Inv_A}("\hspace{-0.05cm}1\hspace{0.03cm}1")\hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(\alpha + 1) = \big[(-\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] + \big[(-1) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] =2\alpha + 2 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}\hspace{-0.05cm}2\hspace{0.03cm}2\hspace{-0.1cm}"\hspace{0.05cm},$$

$${\rm Inv_A}("\hspace{-0.05cm}2\hspace{0.03cm}2")\hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm Inv_A}(2\alpha + 2) = \big[(-2\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] + \big[(-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] =\alpha + 1 \hspace{0.25cm} \Rightarrow \hspace{0.25cm}{\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}\hspace{-0.05cm}1\hspace{0.03cm}1\hspace{-0.1cm}"\hspace{0.05cm}.$$

Consequently, only the first two proposed solutions are correct.

However, the exercise can also be solved without calculation using the addition table alone:

For example, you can find the inverse of "$2\hspace{0.03cm}2$" by looking for the column with the entry "$0\hspace{0.03cm}0$" in the last row.

You find the column labeled "$1\hspace{0.03cm}1$" and thus ${\rm Inv_A}("\hspace{-0.15cm}2\hspace{0.03cm}2\hspace{-0.15cm}") = \, "\hspace{-0.15cm}1\hspace{0.03cm}1\hspace{-0.15cm}"$.

(5) Multiplying $\alpha$ $($vector "$1\hspace{0.03cm}0$"$)$ by itself gives $\alpha^2$.

If the first proposed solution were valid, the condition $\alpha^2 + 2 = 0$ and thus $\alpha^2 = (-2) \, {\rm mod} \, 3 = 1$, thus yielding the vector "$0\hspace{0.03cm}1$".

Assuming the second proposed solution, it follows from the condition $\alpha^2 + 2\alpha + 2 = 0$ in polynomial notation:

$$\alpha^2 = \big [(-2\alpha) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big] + \big[(-2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3\big ] = \alpha + 1 $$

and thus the coefficient vector "$1\hspace{0.03cm}1$".

In the multiplication table, in row 4, column 4, we find exactly the entry "$1\hspace{0.03cm}1$" ⇒ So, the correct answert is the proposed solution 2.

(6) The multiplicative inverse to "$1\hspace{0.03cm}2$" can be found in row 6 of the multiplication table as the column with the entry "$0\hspace{0.03cm}1$"

So the proposed solution 2 is correct in contrast to proposal 3. Namely, ${\rm Inv_M}("\hspace{-0.15cm}21\hspace{-0.15cm}") = \, "\hspace{-0.15cm}2\hspace{0.03cm}0\hspace{-0.1cm}"$ holds.

We check these results considering $\alpha^2 + 2\alpha + 2 = 0$ by multiplications:

$$"\hspace{-0.15cm}1\hspace{0.03cm}2\hspace{-0.1cm}" \hspace{0.05cm}\cdot \hspace{0.05cm}"\hspace{-0.15cm}1\hspace{0.03cm}0\hspace{-0.1cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm} (\alpha + 2) \cdot \alpha = \alpha^2 + 2\alpha = (-2\alpha-2) + 2\alpha = -2 \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = 1 \hspace{0.15cm} \Rightarrow \hspace{0.15cm} {\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}0\hspace{0.03cm}1\hspace{-0.15cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm multiplicative \hspace{0.15cm}inverse}\hspace{0.05cm}.$$

$$"\hspace{-0.15cm}2\hspace{0.03cm}1\hspace{-0.1cm}" \hspace{0.05cm}\cdot \hspace{0.05cm}"\hspace{-0.15cm}1\hspace{0.03cm}2\hspace{-0.1cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm} (2\alpha + 1) \cdot (\alpha + 2) = 2 \alpha^2 + \alpha + 4\alpha + 2 = 2 \alpha^2 + 5\alpha + 2 = 2 \cdot (-2\alpha - 2) + 5\alpha + 2 = (\alpha - 2) \hspace{0.1cm}{\rm mod} \hspace{0.1cm} 3 = \alpha +1 $$

$$\hspace{2.725cm} \Rightarrow \ {\rm vector}\hspace{0.15cm}"\hspace{-0.15cm}1\hspace{0.03cm}1\hspace{-0.15cm}" \hspace{0.15cm} \Rightarrow \hspace{0.15cm}{\rm no\hspace{0.15cm}multiplicative \hspace{0.15cm}inverse}\hspace{0.05cm}.$$

The solution suggestion 1 is therefore not correct, because there is no multiplicative inverse for "$00$".

(7) The two expressions agree ⇒ YES, as the following calculations show:

$$("\hspace{-0.15cm}20\hspace{-0.1cm}" + "\hspace{-0.15cm}12\hspace{-0.1cm}") \ \cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}02\hspace{-0.1cm}"\cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}21\hspace{-0.1cm}"\hspace{0.05cm},$$

$$"\hspace{-0.15cm}20\hspace{-0.1cm}" \cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" + "\hspace{-0.15cm}12\hspace{-0.1cm}" \cdot "\hspace{-0.15cm}12\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}02\hspace{-0.1cm}" + "\hspace{-0.15cm}22\hspace{-0.1cm}" \hspace{-0.15cm} \ = \ \hspace{-0.15cm} "\hspace{-0.15cm}21\hspace{-0.1cm}"\hspace{0.05cm}.$$

This means: The distributive law has been proved at least on a single example.

	The neutral element of addition is $N_{\rm A} = \,$ "$0\hspace{0.03cm}0$",
	The neutral element of addition is $N_{\rm A} = \,$ "$0\hspace{0.03cm}1$".

	The neutral element of multiplication is $N_{\rm M} = \,$ "$0\hspace{0.03cm}0$",
	The neutral element of multiplication is $N_{\rm M} = \,$ "$0\hspace{0.03cm}1$".

	It holds ${\rm Inv_A} ($"$0\hspace{0.03cm}2$") $\, = \, $ "$0\hspace{0.03cm}1$",
	It holds ${\rm Inv_A} ($"$1\hspace{0.03cm}1$") $\, = \, $ "$2\hspace{0.03cm}2$",
	It holds ${\rm Inv_A} ($"$2\hspace{0.03cm}2$") $\, = \, $ "$0\hspace{0.03cm}0$".

	The multiplication is defined here modulo $p(\alpha) = \alpha^2 + 2$.
	The multiplication is defined here modulo $p(\alpha) = \alpha^2 + 2\alpha + 2$.

	There is a multiplicative inverse for all elements $z_i ∈ {\rm GF}(P^m)$ .
	It holds ${\rm Inv_M} ($"$1\hspace{0.03cm}2$") $\, = \, $"$1\hspace{0.03cm}0$".
	It holds ${\rm Inv_M} ($"$2\hspace{0.03cm}1$") $\, = \, $ "$1\hspace{0.03cm}2$".

	Yes.
	No.