Exercise 2.11: Reed-Solomon Decoding according to "Erasures"

${\rm GF}(2^3)$, represented as powers, polynomials, coefficient vectors

We consider here an encoding and decoding system corresponding to the "graph in the theory section for this chapter".

The Reed–Solomon code is given by the generator matrix $\mathbf{G}$ and the parity-check matrix $\mathbf{H}$ where all elements are from the Galois field $\rm GF(2^3) \ \backslash \ \{0\}$:

$${ \boldsymbol{\rm G}} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} 1 & 1 & 1 & 1 & 1 & 1 & 1\\ 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm},$$

$${ \boldsymbol{\rm H}} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ 1 & \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \hspace{0.05cm}.$$

All code symbols $c_i ∈ \{0, \, 1, \, \alpha, \, \alpha^2, \, \alpha^3, \, \alpha^4, \, \alpha^5, \, \alpha^6\}$ are represented by $m = 3$ bits and transmitted via the erasure channel $(m–\rm BEC)$. A code symbol is already marked as an erasure $\rm E$ if one of the three associated bits is uncertain.

The "code word finder" $\rm (CWF)$ has the task of generating the regenerated code word $\underline{z}$ from the partially erased received word $\underline{y}$. It must be ensured that the result $\underline{z}$ is indeed a valid Reed–Solomon code word.

If the received word $\underline{y}$ contains too many erasures, the decoder outputs a message of the type "symbol cannot be decoded". So no attempt is made to estimate the code word. If $\underline{z}$ is output, this is also correct: $\underline{z} = \underline{c}$.

The sought information value $\underline{v} = \underline{u}$ results from the inverse encoder function $\underline{v} = {\rm enc}^{-1}(\underline{z})$. With the generator matrix $\mathbf{G}$ this can be realized as follows:

$$\underline{c} = {\rm enc}(\underline{u}) \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \underline{u} \cdot {\boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{z} = {\rm enc}(\underline{v}) = \underline{v} \cdot {\boldsymbol{\rm G}} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline{v} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} {\rm enc}^{-1}(\underline{z}) = \underline{z} \cdot {\boldsymbol{\rm G}}^{\rm T}\hspace{0.05cm}.$$

Hints:

This exercise refers to the chapter "Reed–Solomon Decoding for the Erasure Channel".

Regarding the code word finder, we refer in particular to the pages

"Decoding procedure ...", and

"Solution of the matrix equations ...".

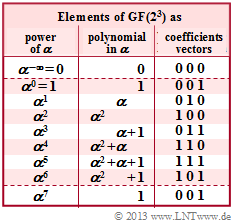
All calculations are to be performed in $\rm GF(2^3)$. The upper graph describes their $q = 8$ elements in power, polynomial and coefficient vector representation.

Questions

Solution

(1) The number of columns of the parity-check matrix $\mathbf{H}$ indicates the code length: $n \ \underline{= 7}$.

The same result is obtained if we assume the order $q = 8$ of the Galois field. For the Reed–Solomon codes $n = q - 1$ is valid.
The number of rows of the parity-check matrix is equal to $n - k = 3 \ \Rightarrow \ k \ \underline{= 4}$.
Of all Reed–Solomon codes, the "Singleton bound" is satisfied ⇒ $d_{\rm min} = n - k + 1 \ \underline{= 4}$.
Thus, it is the Reed–Solomon code $(7, \, 4, \, 4)_8$.

(2) Decoding is certainly possible as long as the number $e$ of extinctions is smaller than the minimum distance $d_{\rm min}$. This condition is fulfilled here ⇒ YES.

Since the null word is allowed in all RS codes and every other codeword contains at least four symbols not equal to "$0$", it is already certain without calculation that the null word was sent.
The formal calculation confirms this result:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} \alpha^6\\ \alpha^{5}\\ \alpha^{4} \end{pmatrix} \cdot z_6 = \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \hspace{0.3cm} \Rightarrow \hspace{0.3cm} z_6 = 0 \hspace{0.05cm}. $$

(3) Again $e = 2$ is smaller than $d_{\rm min} = 4$ ⇒ YES.

Since $(1, \, 1, \, 1, \, 1, \, 1, \, 1, \, 1)$ is also a valid codeword, we expect $z_0 = 1$ und $z_1 = 1$ in the formal verification.

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ \alpha^4 & \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ \alpha^6 & \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \cdot\begin{pmatrix} 1\\ 1\\ 1\\ 1\\ 1 \end{pmatrix}= \begin{pmatrix} \alpha^2 + \alpha^3 + \alpha^4 + \alpha^5 + \alpha^6\\ \alpha^4 + \alpha^6 + \alpha^1 + \alpha^{3} + \alpha^{5}\\ \alpha^6 + \alpha^2 + \alpha^{5} + \alpha^{1} + \alpha^{4} \end{pmatrix}$$

$$\Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \begin{pmatrix} (100) + (011) + (110) + (111) + (101)\\ (110) + (101) + (010) + (011) + (111)\\ (101) + (100) + (111) + (010) + (110) \end{pmatrix} = \begin{pmatrix} (011)\\ (101)\\ (010) \end{pmatrix} = \begin{pmatrix} \alpha^3\\ \alpha^6\\ \alpha^1 \end{pmatrix} \hspace{0.05cm}. $$

In this calculation, we varied between the polynomial representation and the coefficient representation on the data side. Thus the system of equations reads:

$$\begin{pmatrix} (001) + (010) \\ (001) + (100)\\ (001) + (011) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1 \end{pmatrix} = \begin{pmatrix} (011)\\ (101)\\ (010) \end{pmatrix} \hspace{0.25cm} \Rightarrow \hspace{0.25cm} \begin{pmatrix} (001) + (010) \\ (001) + (100)\\ (000) + (111) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1 \end{pmatrix} = \begin{pmatrix} (011)\\ (101)\\ (111) \end{pmatrix}\hspace{0.05cm}.$$

The second form is obtained by substituting the third row from the modulo $2$ sum of rows 2 and 3.
From the last row now follows $z_1 = 1$ and the rows 1 and 2 are then:

$$(1)\hspace{0.3cm}z_0 + (010) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (011)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm},$$

$$(2)\hspace{0.3cm}z_0 + (100) \cdot 1 \hspace{-0.15cm} \ = \ \hspace{-0.15cm} (101)\hspace{0.3cm} \Rightarrow \hspace{0.3cm}z_0 = (001) = 1\hspace{0.05cm}. $$

Both equations lead to the same result $z_0 = 1, \ z_1 = 1$. The decoding is successful.

(4) Decoding happens on following steps:

$${ \boldsymbol{\rm H}}_{\rm K} \cdot \underline {z}_{\rm K}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6\\ \alpha^6 & \alpha^1 & \alpha^{3} & \alpha^{5}\\ \alpha^2 & \alpha^{5} & \alpha^{1} & \alpha^{4} \end{pmatrix} \cdot\begin{pmatrix} 0\\ 1\\ \alpha\\ 0 \end{pmatrix}= \begin{pmatrix} \alpha^4 + \alpha^6\\ \alpha^1 + \alpha^{4}\\ \alpha^5 + \alpha^2 \end{pmatrix}= \begin{pmatrix} (110) + (101)\\ (010) + (110)\\ (111) + (100) \end{pmatrix} = \begin{pmatrix} (011)\\ (100)\\ (011) \end{pmatrix} \hspace{0.05cm},$$

$${ \boldsymbol{\rm H}}_{\rm E} \cdot \underline {z}_{\rm E}^{\rm T} \hspace{-0.15cm} \ = \ \hspace{-0.15cm} \begin{pmatrix} 1 & \alpha^1 & \alpha^2\\ 1 & \alpha^2 & \alpha^4\\ 1 & \alpha^3 & \alpha^6 \end{pmatrix} \cdot\begin{pmatrix} z_0\\ z_1\\ z_2 \end{pmatrix}\hspace{0.3cm} \Rightarrow \hspace{0.3cm} \begin{pmatrix} (001) &(010) &(100)\\ (001) &(100) &(110)\\ (001) &(011) &(101) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1\\ z_2 \end{pmatrix}= \begin{pmatrix} (011)\\ (100)\\ (011) \end{pmatrix} \hspace{0.05cm}. $$

We now replace row 2 with the modulo $2$ sum of rows 1 and 2, and row 3 with the modulo $2$ sum of rows 1 and 3:

$$\begin{pmatrix} (001) &(010) &(100)\\ (000) &(110) &(010)\\ (000) &(001) &(001) \end{pmatrix} \cdot \begin{pmatrix} z_0\\ z_1\\ z_2 \end{pmatrix}= \begin{pmatrix} (011)\\ (111)\\ (000) \end{pmatrix} \hspace{0.05cm}.$$

From the last row follows $z_1 + z_2 = 0 \ \Rightarrow \ z_2 = z_1$. Substituting into the second row of this matrix equation we get:

$$\big[(110) + (010)\big] \cdot z_1 = (100) \cdot z_1 = (111) \hspace{0.2cm} \Rightarrow \hspace{0.2cm} \alpha^2 \cdot z_1 = \alpha^5\hspace{0.2cm}\Rightarrow \hspace{0.2cm} z_1 \hspace{0.1cm}\underline{= \alpha^3}\hspace{0.05cm},\hspace{0.2cm}z_2 \hspace{0.1cm}\underline{= \alpha^3} \hspace{0.05cm}. $$

With this result follows from the first matrix row:

$$z_0 + \big[(010) + (100)\big] \cdot z_1 = z_0 + (110) \cdot z_1 = (011) $$

$$\Rightarrow \hspace{0.2cm} z_0 + \alpha^4 \cdot \alpha^3 = z_0 + 1 = \alpha^3 \hspace{0.2cm} \Rightarrow \hspace{0.2cm} z_0 = \alpha^3 + 1 = ( \alpha + 1) +1\hspace{0.15cm} \underline{= \alpha}\hspace{0.05cm}.$$

The correct solution is therefore proposed solution 2.

(5) Correct is proposed solution 4. Reason:

Four information symbols cannot be obtained from the three known symbols $0, \, 1, \, \alpha$.
The $\mathbf{H}$ matrix of this $(7, \, 4, \, 4)_8$ code has exactly $n - k = 3$ rows.
This also means that you have only three equations. But you would need four equations for the unknowns $z_0, \ z_1, \ z_2$ and $z_6$.

	$z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = 0$.
	$z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = \alpha^3$.
	$z_0 = 1, \ z_1 = 0, \ z_2 = \alpha^3$.
	The decoding does not lead to any result.

	$z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = 0, \ z_6 = 1$.
	$z_0 = \alpha, \ z_1 = \alpha^3, \ z_2 = \alpha^3, \ z_6 = 1$.
	$z_0 = 1, \ z_1 = 0, \ z_2 = \alpha^3, \ z_6 = 1$.
	The decoding does not lead to any result.

	YES.
	NO.

	YES.
	NO.