Error Correction According to Reed-Solomon Coding

1. Channel Coding
2. Reed–Solomon–Codes and Their Decoding
3. Error Correction According to Reed-Solomon Coding

• Previous page
• Next page

• Previous page
• Next page

Block diagram and requirements for RS error correction

As in the chapter  "Decoding at the Erasure Channel"  we consider a transmission system with Reed–Solomon coding characterized by the two code parameters  $n=2^m-1$  and  $k$.  With the generator matrix  $\boldsymbol{\rm G}$  the relation between the information word  $\underline {u}$  and the code word  $\underline {c}$  is:

Transmission system with Reed-Solomon coding/decoding and $m$– BSC

$$\underline {c} = {\rm enc}(\underline {u}) = \underline {u} \cdot { \boldsymbol{\rm G}} \hspace{0.3cm} {\rm with}$$

$$ \underline {u} = (u_0, u_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, u_{k-1})\hspace{0.05cm},$$

$$ \underline {c} = (c_0, c_1, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_i, \hspace{0.05cm}\text{...} \hspace{0.05cm}, c_{n-1}) \hspace{0.05cm}.$$

The symbols  $u_i$  and  $c_i$  originate from the field  ${\rm GF}(q)$  with 

$$q=n+1=2^m.$$

They are representable by  $m$  binary symbols  ("bits").

A comparison of the upper block diagram with the corresponding  "block diagram for RS fault detection"  shows:

• The main difference is in the discrete channel model used (highlighted in green). Instead of the erasure channel  ("$m$ BEC")  now the  $m$ BSC  is considered. For each bit of the code symbol  $c_i$  the  Binary Symmetric Channel  (BSC) is applied. A bit error with respect to the $i$ bit results in  $y_i \ne c_i$.
  

• In the  "last chapter"  uncertain bits were already marked by erasures  $\rm E$. The exercise of the  code word finder  $\rm (CWF)$ was to reconstruct the decoding result  $\underline {y}$  from the garbled received words  $\underline {z}$ .
• If the number  $e$  of extinctions is smaller than the minimum distance  $d_{\rm min}$, this succeeds and we get  $\underline {z} = \underline {c}$. Otherwise, the codeword finder reports that it cannot decode the current received word  $\underline {y}$ .   A wrong decision  $(\underline {z} \ne \underline {c})$  was excluded at the BEC.
  

• In this chapter, the first decoder block is now referred to as  code word estimator  $\rm (CWS)$. The naming is to make clear that due to the  $m$ BSC model, wrong decisions  $(\underline {z} \ne \underline {c})$  are inevitable, namely when multiple symbol errors distort the received word  $\underline {y}$  to a valid codeword.
  
  

$\text{Conclusion:}$ 

• The decoder's exercise is to determine its output vector  $\underline {v}$  so that it matches the information word  $\underline {u}$  "as well as possible". More precisely formulated:

\[{ \rm Pr(Block\hspace{0.15cm}error)} = { \rm Pr}( \underline{v} \ne \underline{u}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]

• Because of deterministic mapping  $\underline{c} = {\rm enc}(\underline{u})$  and  $\underline{v} = {\rm enc}^{-1}(\underline{z})$  holds in the same way:

\[{ \rm Pr(Block\hspace{0.15cm}error)} = { \rm Pr}( \underline{z} \ne \underline{c}) \stackrel{!}{=} { \rm Minimum}\hspace{0.05cm}.\]

The two blocks highlighted in yellow are not considered further below. The focus of the considerations is now the code word estimator  $\rm (CWS)$ highlighted in red.

Possible code word estimators for RS decoding

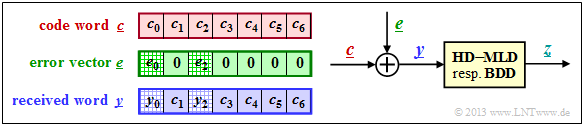
The right sketch of the following graphic illustrates the task again, where here the channel model "$m$ BSC" is replaced by the additive  error vector  $\underline{e} = \underline{y} - \underline{c}$ . The sketch on the left illustrates the relationship between these three vectors.

Definition of the error vector  $\underline{e}$

This task is to be clarified by an example.

Three forms of representation for $\rm GF(2^3)$

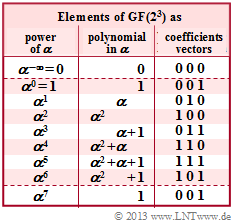
$\text{Example 1:}$  Let all symbols be elements of  $\rm GF(2^3) \in \{0, 1, \alpha^1, \alpha^2, \alpha^3, \alpha^4, \alpha^5, \alpha^6\}$. For conversion

• between the coefficient representation $($with the order  $k_2$,  $k_1$,  $k_0)$
• and the exponent representation $($as powers of the primitive element  $\alpha)$

the adjacent table can be used.

In this example, the codeword and received words are in coefficient notation:

\[\underline{c} = \Big ( (010), (001), (100),(010),(100),(111),(111)\Big )\hspace{0.05cm},\]

\[\underline{y} =\Big ( (011), (001), (000),(010),(100),(111),(111)\Big )\hspace{0.05cm}.\]

This results in the following for the error vector  $\underline{e} = \underline{y} - \underline{c}$:

\[\underline{e} \hspace{0.05cm} = \hspace{0.05cm} \Big ( (001), (000), (100), (000),(000),(000),(000)\Big )\hspace{0.05cm}.\]

Converted to the exponential representation, we get:

\[\underline{c} = \Big ( \alpha^1, \hspace{0.09cm}1\hspace{0.09cm}, \alpha^2,\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big )\hspace{0.05cm},\]

\[\underline{y} =\Big ( \alpha^3, \hspace{0.09cm}1\hspace{0.09cm}, \hspace{0.09cm}0\hspace{0.09cm},\alpha^1,\alpha^2,\alpha^5,\alpha^5\Big )\hspace{0.05cm},\]

\[\underline{e} = \Big ( \hspace{0.09cm}1\hspace{0.09cm}, \hspace{0.09cm}0\hspace{0.09cm}, \hspace{0.05cm}\alpha^2,\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm},\hspace{0.12cm}0\hspace{0.12cm}\Big )\hspace{0.05cm}.\]

The task of the code word estimator  $\rm (CWS)$  is to find the most probable code word to  $\underline{y}$  and to pass its result  $\underline{z} = \underline{c}_i$  to the following mapping. There are several ways to do this:

• Hard Decision Maximum Likelihood Decoding  $\text{(HD MLD)}$,
  

• Bounded Distance Decoding  $\text{(BDD)}$,
  

• Decoding over half the minimum distance.
  
  

These decoding principles are described below.

Hard Decision Maximum Likelihood Decoding  $\text{(HD MLD)}$:

One chooses from all possible Reed–Solomon codewords  $\underline{c}_i$  $($hierof there are in total  $q^k)$  the one with the least  "Hamming distance"  to the received word  $\underline{y}$  from. Thus the result is:

\[\underline{z} = {\rm arg} \min_{\underline{c}_{\hspace{0.03cm}i} \hspace{0.05cm} \in \hspace{0.05cm} \mathcal{C}_{\rm RS}} \hspace{0.1cm} d_{\rm H}(\underline{y} \hspace{0.05cm}, \hspace{0.1cm}\underline{c}_{\hspace{0.03cm}i})\hspace{0.05cm}.\]

The decision here happens on the maximum inference probability  ${\rm Pr}(\underline{c}_i\hspace{0.05cm}|\hspace{0.05cm}\underline{y})$  and leads to the best possible result. For more details see  "ML Decision at the BSC Channel". A decision is always made even if the number  $r$  of symbol errors is larger than the correction capability  $t$  of the code. However, in such a case the decoding result is very uncertain.

• It should be mentioned again that maximum likelihood decoding always decides.
• Decoding failure is impossible.
• But of course there are also wrong decisions.
  
  

Bounded Distance Decoding  $\text{(BDD)}$:

If the number  $r$  of symbol errors in the received words  $\underline{y}$  is not greater than the correction capability  $t = ⌊(d_{\rm min}- 1)/2⌋$  of the code, one can correct the  $r$  symbol errors completely. However, it is also true:

• The case  $r > t$  leads to an abort of the decoding process with no result.   In other words:
• Only those received words towards the center of the sphere are decoded, which lie in a sphere around it with radius  $t$ .
• Other received words are marked as undecodable, for example as erasure.
  
  

Decoding over half the minimum distance:

Here also in the case  $r > t$  an attempt is made to decode the codeword. In contrast to  $\text{HD MLD}$, which also decodes beyond half the minimum distance, a decoding failure is not per se excluded here, however.

For the remainder of this chapter, we will deal exclusively with Bounded Distance Decoding. The reason for this is the enormous complexity of Maximum Likelihood Decoding  proportional to  $q^{n-k}$.

Bounded Distance Decoding Procedure

In the following, the individual steps of the BDD algorithm are described briefly and in a recipe-like manner. On the following pages, the individual points will be dealt with in more detail and the procedure will be illustrated using typical examples.

$\rm (A)$   $\text{Calculation and evaluation of syndrome}$   ⇒   "Detailed description"

• Calculate from the received word  $\underline{y}$  and the parity-check matrix  $\boldsymbol{\rm H }$  of the code the syndrome  $\underline {s} = \underline {y} \cdot \boldsymbol{\rm H }^{\rm T}$.
• If  $\underline {s} =\underline {0}$, set the BDD output  $\underline {z} =\underline {y}$  and terminate the decoding process for that received word.
  
• Otherwise set the parameter  $r = 1$  and continue with step  $\rm (B)$ .
  
  

$\rm (B)$   $\text{Determine the actual symbol error count } r$  ⇒   "Detailed description"

• Create and check the equations  $\underline {\it \Lambda} _l \cdot\underline {s}^{\rm T} = 0$   for   $l = 1,$ ... , $2 \cdot t -r$  assuming that the received word contains exactly   $r$   symbol errors.
  

• $\underline {\it \Lambda} _l $  denotes the generalized  $\text{ELP}$ coefficient vectors, where "$\text{ELP}$" stands for  "Error Locator Polynomial"  and  $t$  denotes the correctability of the code.
  For the Reed–Solomon codes, uniformly  $t = ⌊(n-k)/2 ⌋$.
  

• If there is a unique solution, then continue with step  $\rm (C)$ .  In the received vector  $\underline{y}$  there are then indeed exactly  $r$  symbols corrupted and in the error vector  $\underline{e}$  there are  $r$  entries not equal to $0$.
  

• Otherwise increase  $r$  by  $1$.   If  $r ≤ t$, then repeat step  $\rm (B)$  from the beginning:   The previously assumed  $r$  was obviously too small. Therefore now a new attempt with larger  $r$.
  

• If the new  $r$  is greater than the correction capability  $t$  of the code, the current received word cannot be decoded. End the decoding attempt with an  error message.
  
  

$\rm (C)$   $\text{Localization of the }r \text{ error locations}$  ⇒   "Detailed description"

• Create the  error locator polynomial  ${\it \Lambda}(x)$  and find its  $r$  zeros in  ${\rm GF}(q) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\}$.
  

• An error at location  $i$  is present whenever  ${\it \Lambda}(\alpha^{i}) = 0$ .
  
  

$\rm (D)$   $\text{Determination of }r \text{ error values and correction}$  ⇒   "Detailed description"

• Now the  $r$  error locations are known. Replacing in the received vector  $\underline{y}$  the wrong symbols with erasures   ⇒   $y_i = \rm E$, if  $e_i ≠ 0$, we find the result  $\underline{y}$  corresponding to the chapter  "Reed-Solomon Decoding at the Erasure Channel".
  

• An alternative:   From the equation  $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$  one arrives at a linear system of equations for the faulty symbols  $(e_i = 0)$  taking advantage of the error-free sites  $(e_i \ne 0)$.
  
  

Step (A): Evaluation of the syndrome in BDD

As shown in section  "Principle of Syndrome Decoding"  syndrome  $\underline{s}$  can be used to decode a linear code.

With the received word  $\underline{y}$  equal to codeword  $\underline{c}$  plus error vector  $\underline{e}$  applies:

\[\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H }}^{\rm T}= \underline {c} \cdot { \boldsymbol{\rm H }}^{\rm T}+ \underline {e} \cdot { \boldsymbol{\rm H }}^{\rm T} \hspace{0.05cm}.\]

Since always  $\underline {c} \cdot { \boldsymbol{\rm H }}^{\rm T} =\underline {0}$  holds, it follows from  $\underline{s}= \underline{0}$  also  $\underline {e} \cdot { \boldsymbol{\rm H }}^{\rm T} =\underline{0}$.   That is:

• With very high probability, from  $\underline{s}= \underline{0}$  it is also possible to infer  $\underline{e}= \underline{0}$  and thus also the correct decoding result  $\underline{z}= \underline{y}$  . The decoding process would be finished.
  

• But there are also error patterns  $\underline{e} \ne \underline{0}$ that lead to the syndrome  $\underline{s}= \underline{0}$ . Such patterns certainly contain more than  $t$  symbol errors, so here too it makes sense to abort the decoding process. All subsequent calculations would also not lead to success.
  
  

$\rm GF(2^3)$ representations

$\text{Example 2:}$  This and the following examples on the next pages are always based on the Reed–Solomon code  $\text{RSC (7, 3, 5)}_8$  so that the conversions given in the graph in  $\rm GF(2^3)$  can be used. The received words are:

\[\underline{y}=\big (\alpha^3,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}\alpha^1, \hspace{0.05cm} \alpha^2, \hspace{0.05cm} \alpha^5, \hspace{0.05cm} \alpha^5 \big).\]

With the  "Parity-Check Matrix"  $\boldsymbol{\rm H }$  results for the syndrome:

\[\underline {s} = \underline {y} \cdot { \boldsymbol{\rm H } }^{\rm T}= \begin{pmatrix} \alpha^3, \hspace{0.05cm}1, \hspace{0.05cm}0, \hspace{0.05cm}\alpha^1, \hspace{0.05cm}\alpha^2, \hspace{0.05cm}\alpha^5, \hspace{0.05cm}\alpha^5 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 \\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 \\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^5 \\ \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 \\ \alpha^5 & \alpha^3 & \alpha^1 & \alpha^6 \\ \alpha^6 & \alpha^5 & \alpha^4 & \alpha^3 \end{pmatrix}. \]

These vector–matrix multiplications gives the result:

\[\underline {s} \hspace{-0.05cm} = \hspace{-0.05cm} (\alpha^3 , \alpha^3 , \alpha^3 , \alpha^3) + (\alpha^1 , \alpha^2 , \alpha^3 , \alpha^4) + (0,0,0,0) \hspace{-0.05cm}+\hspace{-0.05cm} (\alpha^4,1,\alpha^3,\alpha^6)+(\alpha^6,\alpha^3,1,\alpha^4)\hspace{-0.05cm}+\hspace{-0.05cm}(\alpha^3,\alpha^1,\alpha^6,\alpha^4) \hspace{-0.05cm}+\hspace{-0.05cm} (\alpha^4,\alpha^3,\alpha^2,\alpha^1)\]

\[\Rightarrow \hspace{0.3cm} \underline {s} = \text{...} \hspace{0.05cm}= (\alpha^5,\alpha^2,\alpha^3,\alpha^1) \hspace{0.05cm}.\]

So the received word was corrupted.   Otherwise it should have resulted in  $\underline{e}= \underline{0} = (0, 0, 0, 0)$ .

The description of the decoding process at  $\text{RSC (7, 3, 5)}_8$  is continued in  "$\text{Example 4}$" 

Error Locator Polynomial - Definition and Properties

After the syndrome calculation in step  $\rm (A)$  with the result  $\underline{s} \ne \underline{0}$  we know,

• that the received word  $\underline{y}$  does not match the codeword  $\underline{c}$  respectively
  

• that the error vector  $\underline{e} = (e_0, \hspace{0.05cm}e_1, \hspace{0.05cm}\text{ ...}\hspace{0.05cm} , e_{n-1})$  certainly includes elements not equal to  $0$ .
  
  

However, we do not know how many symbols were corrupted  $(0 < r ≤ n)$  nor can we name the positions of the error locations  $(e_i ≠ 0)$  in the error vector  $\underline{c}$ .

An approach to this exercise is provided by the so-called  Error Locator Polynomial introduced by  "William Wesley Peterson"  ⇒   see [Pet60]. It is also known as key equation.

$\text{Definition:}$  Let it be known that exactly  $r$  elements of the error vector  $\underline{e}$  are non-zero, recognizable by  "Hamming weight"  $w_{\rm H}(\underline{e}) = r$.

• Also let the quantity  ${I}_{\rm FP}$  of error positions be known:

\[I_{\rm FP} = \{ i \hspace{0.1cm}\vert \hspace{0.1cm} e_i \ne 0,\hspace{0.1cm} 0 \le i < n \}\hspace{0.05cm}.\]

• Then for the  Error Locator Polynomial  $\rm (ELP)$:

\[{\it \Lambda}(x)=x \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm FP} }(x-\alpha^i) =x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ].\]

From the error locator polynomial  we know because of the definition:

• because of the factor  $x$  in front of the product sign is  ${\it \Lambda}(x= 0) = 0$.
  

• Other  $r$  zeros result for  $x = \alpha^{i}$  with  $i \in I_{\rm FP}$, that is, for all error positions.
  

• In contrast, the  error locator polynomial  for  $i ∉ yields I_{\rm FP}$   ⇒   $e_i = 0$  no zero:   ${\it \Lambda}(x= \alpha^{i}) \ne0$.
  
  

So we search for the  $r$  nontrivial zeros of  ${\it \Lambda}(x)$  with the argument  $x ∈ {\rm GF}(q) \hspace{-0.05cm}\setminus \hspace{-0.05cm} \{0\}$. If we succeed, we know the  $r$  error positions, but not yet the actual error values  $e_i ∈ {\rm GF}(q)$.

$\rm GF(2^3)$ representations

$\text{Beispiel 3:}$  Let $n=7$   ⇒   $q=8$,  $r=2$  and  $I_{\rm FP} = \{2, \hspace{0.05cm}4\}$:        

Thus for the  error locator poynomial  from  ${\rm GF}(2^3)$ is obtained:

\[{\it \Lambda}(x)=x \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}-\hspace{-0.05cm}\alpha^4)= x \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^2) \cdot (x\hspace{-0.05cm}+\hspace{-0.05cm}\alpha^4) =x \cdot \big [x^2 \hspace{-0.05cm}+ \hspace{-0.05cm}(\alpha^2 + \alpha^4) \cdot x + \alpha^6\big ] \]

\[\Rightarrow \hspace{0.3cm} {\it \Lambda}(x)= x \cdot \big [\alpha^6 + \alpha \cdot x + x^2\big ]\hspace{0.05cm}.\]

The other zeros $($except for  $x = 0)$  arise naturally here for  $x = \alpha^2$  and  $x = \alpha^4$, as a calculation shows:

\[{\it \Lambda}(x = \alpha^2)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^2 + (\alpha^2)^2\big ] = x \cdot \big [\alpha^6 + \alpha^3 + \alpha^4 \big ]= 0\hspace{0.05cm},\]

\[ {\it \Lambda}(x = \alpha^4)= x \cdot \big [\alpha^6 + \alpha \cdot \alpha^4 + (\alpha^4)^2\big ] =x \cdot \big [\alpha^6 + \alpha^5 + \alpha \big ]= 0\hspace{0.05cm}.\]

For further derivation, we always assume the  $\text{RSC (7, 3, 5)}_8$  with the following parameter values:

$$n=7, \hspace{0.3cm}k = 3, \hspace{0.3cm}d_{\rm min} = 5 \ \Rightarrow \ t = (d_{\rm min} -1/2) = 2.$$

Let the number of symbol errors be  $r = t = 2$. Thus the system of equations to be solved with the auxiliary variables  $L_i = {\it \Lambda}(\alpha^{i})$:

\[L_0 = {\it \Lambda }(\alpha^0) = \alpha^0 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^0)^1 + (\alpha^0)^2 \right ] = {\it \lambda}_0 \cdot 1 + {\it \lambda}_1 \cdot 1 + 1 \hspace{0.05cm},\]

\[L_1 = {\it \Lambda }(\alpha^1) =\alpha^1 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^1)^1 + (\alpha^1)^2 \right ] = {\it \lambda}_0 \cdot \alpha^1+ {\it \lambda}_1 \cdot \alpha^2 + \alpha^3 \hspace{0.05cm},\]

\[...\]

\[ L_6 = {\it \Lambda }(\alpha^6) = \alpha^6 \cdot \left [ {\it \lambda}_0 + {\it \lambda}_1 \cdot (\alpha^6)^1 + (\alpha^6)^2 \right ] = {\it \lambda}_0 \cdot \alpha^6 + {\it \lambda}_1 \cdot \alpha^{12} + \alpha^{18} \hspace{0.05cm}.\]

In vector form, this system of equations with the auxiliary vector is  $\underline{L} = (L_0, \hspace{0.05cm}L_1, \hspace{0.05cm}L_2,\hspace{0.05cm}L_3,\hspace{0.05cm}L_4,\hspace{0.05cm}L_5,\hspace{0.05cm}L_6)$:

\[\underline {L}^{\rm T}=\begin{pmatrix} L_0\\ L_1\\ L_2\\ L_3\\ L_4\\ L_5\\ L_6 \end{pmatrix} \hspace{0.15cm} = \hspace{0.15cm} \begin{pmatrix} 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 \\ \alpha^2 & \alpha^4 & \alpha^6 \\ \alpha^3 & \alpha^6 & \alpha^9 \\ \alpha^4 & \alpha^8 & \alpha^{12}\\ \alpha^5 & \alpha^{10} & \alpha^{15}\\ \alpha^6 & \alpha^{12} & \alpha^{18} \end{pmatrix} \hspace{0.15cm}\cdot \hspace{0.15cm} \begin{pmatrix} {\lambda}_0\\ {\lambda}_1\\ 1 \end{pmatrix} \hspace{0.05cm}.\]

We now expand the ELP coefficient vector  $\underline {\it \Lambda }$  by appending zeros to the length  $n-k$.

Thus, in the considered example, we obtain  ${\it \Lambda } = ( \lambda_0,\hspace{0.05cm}\lambda_1,\hspace{0.05cm}1, \hspace{0.05cm}0)$  and the following vector equation:

\[\underline {L}^{\rm T} \hspace{0.15cm} = \hspace{0.15cm} \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^8\\ \alpha^3 & \alpha^6 & \alpha^9 & \alpha^{12}\\ \alpha^4 & \alpha^8 & \alpha^{12} & \alpha^{16}\\ \alpha^5 & \alpha^{10} & \alpha^{15} & \alpha^{20}\\ \alpha^6 & \alpha^{12} & \alpha^{18} & \alpha^{24} \end{pmatrix} \hspace{0.15cm}\cdot \hspace{0.15cm} \begin{pmatrix} {\lambda}_0\\ {\lambda}_1\\ 1\\ 0 \end{pmatrix} \hspace{0.05cm}.\]

With this we have achieved:

• The  $7× 3$ matrix has now become a  $7× 4$ matrix.
• The fourth column can actually be filled arbitrarily, since all elements are multiplied by zeros.
• The addition chosen here gives the transposed  "parity-check matrix"  of  $\text{RSC (7, 3, 5)}_8$.
• Thus, one can write for the last vector equation:

\[\underline {L}^{\rm T} = { \boldsymbol{\rm H }}^{\rm T} \cdot \underline {\it \Lambda }^{\rm T} \hspace{0.3cm} \Rightarrow \hspace{0.3cm}\underline {L} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \hspace{0.05cm}.\]

But since for the error locations  $(e_i ≠ 0)$  always  $L_i = {\it \Lambda}(\alpha^{i}) = 0$  holds, the product  $L_i \cdot e_i \equiv 0$  and one obtains as determining equation for the zeros of the error locator polynomial:

\[\underline {L}^{\rm T} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }} \cdot \underline {e}^{\rm T} = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 \hspace{0.05cm}.\]

$\text{Important intermediate result:}$ 

The nontrivial zeros  $($equal to $0)$  $\lambda_0$, $\lambda_1$, ... of the error locator polynomial   ${\it \Lambda}(x)$  must always satisfy the vector equation  $\underline {\it \Lambda } \cdot \underline {s}^{\rm T} = 0 $  .

• Hereby denotes  $\underline {\it \Lambda }$  the  $\rm ELP coefficient vector$.
• $\underline {s } = \underline {y }\cdot \boldsymbol{\rm H }^{\rm T} $  gives the  "syndrome" .

Step (B): Set up/evaluate the ELP coefficient vector

Before we can consider this intermediate result for step  $\rm (B)$  some generalizations need to be made. The reason for this is:

• The equation  $\underline {\it \lambda } \cdot \underline {s}^{\rm T} = 0 $  yields only a single equation of determination. Thus the problem can be solved for  $r = 1$  if one is sure that indeed only one symbol has been corrupted.
  

• If one is not sure of this, but nevertheless performs the calculation for  $r = 1$ , one still needs a second equation (or even several) to verify the assumption.
  
  

The property of  "Error Locator Polynomial" that  ${\it \Lambda}(\alpha^{i})$  is zero only for  $e_i ≠ 0$  $(i$–th symbol corrupted$)$ is preserved when multiplying  ${\it \Lambda}(x)$  by arbitrary powers of  $x$ . Each multiplication by  $x$  implies a shift of one place to the right for the ELP coefficient vector.

Shifted ELP coefficient vectors

$\text{Definition:}$  The  $\text{generalized ELP coefficient vectors}$  $\underline {\it \Lambda }_l$  result from successive shifts with respect to  $\underline {\it \Lambda }_l$:

\[{\it \Lambda}_l(x)=x^l \cdot \prod_{i\hspace{0.05cm}\in \hspace{0.05cm} I_{\rm FP} }(x-\alpha^i) =x^l \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+\ldots+{\it \lambda}_{r-1} \cdot x^{r-1}+x^r \big ]\hspace{0.05cm}.\]

In this defining equation,  $\underline {\it \Lambda }_1$  corresponds to the previous  $\underline {\it \Lambda }$.

The graph shows the occupancy under the assumption of  $r$  error locations in the error vector  $\underline {e}$  for

• $r=1$   in the left panel (with blue background),
• $r=2$   in the middle area (with red background),
• $r=3$   in the right area (with green background).

One recognizes:

• The length of all  $\underline {\it \lambda }_l$  is always  $n-k$. Each vector contains respectively  $r$  coefficients  $\lambda_0$,  $\lambda_1$, ... ,  $\lambda_{r-1}$   ⇒   $0 ≤ i < r$  and a one. The remainder of each vector is padded with zeros.
  

• For each  $r$  there are exactly  $n-k-r$  coefficient vectors  $\underline {\it \Lambda }_l$, where  $\underline {\it \Lambda }_l$  results from  $\underline {\it \Lambda }_{l-1}$  always by right shifting by one position. The vector  $\underline {\it \Lambda }_{n-k-r}$  always ends with a  $1$.
  

• The system of equations  $\underline {\it \Lambda }_l \cdot \underline {s}^{\rm T} = 0 $  therefore leads to  $n-k-r$  equations. The chosen approach for  $r$  is correct only if all equations lead to the same results for  $\lambda_0$, ... , $\lambda_{r-1}$ .
  

• If this is not the case, one has to increase  $r$  and thus work on a new system of equations, and this until a unique solution results from all equations for the current  $r$ .
  

• If finally  $r$  is greater than the correctability  $t$  of the code, the calculation can be terminated. The pending received word  $\underline {y}$  is then not decodable.
  

$\text{Example 4:}$  The conditions stated in the  $\text{"Example 2"}$  still apply:

• There, due to the syndrome  $\underline {s} = (\alpha^5,\alpha^2,\alpha^3,\alpha^1) ≠ \underline {0}$  it was also demonstrated that the received vector  $\underline {y}$  was corrupted   ⇒   error vector  $\underline {e} \underline {0}$.
• Not known, however, is the actual symbol error count  $r$.
  

Assuming a single wrong symbol  $(r= 1)$  we obtain the following system of equations (written here in matrix form):

$\rm GF(2^3)$ representations

\[\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= \begin{pmatrix} \lambda_0 & 1 & 0 & 0 \\ 0 & \lambda_0 & 1 & 0 \\ 0 & 0 & \lambda_0 & 1 \end{pmatrix} \cdot \begin{pmatrix} \alpha^5\\ \alpha^2\\ \alpha^3\\ \alpha \end{pmatrix} \stackrel{!}{=} \begin{pmatrix} 0\\ 0\\ 0 \end{pmatrix} \hspace{0.05cm}.\]

This system of equations gives three different solutions for  $\lambda_0$, which is not purposeful:

\[\text{Zeile 1:}\hspace{0.5cm}\alpha^5 \cdot \lambda_0 + \alpha^2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{2-5}= \alpha^{-3}= \alpha^{4}\hspace{0.05cm},\]

\[\text{Zeile 2:}\hspace{0.5cm}\alpha^2 \cdot \lambda_0 + \alpha^3 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{3-2}= \alpha\hspace{0.05cm},\]

\[\text{Zeile 3:}\hspace{0.5cm}\alpha^3 \cdot \lambda_0 + \alpha^1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \lambda_0 = \alpha^{1-3}= \alpha^{-2} = \alpha^{5} \hspace{0.05cm}.\]

Deshalb stellen wir nun ein weiteres Gleichungssystem auf, und zwar unter der Annahme  $r = 2$:

\[\big ({ \boldsymbol{\it \Lambda } }_l \big) \cdot \underline {s} ^{\rm T}= \begin{pmatrix} \lambda_0 & \lambda_1 & 1 & 0 \\ 0 & \lambda_0 & \lambda_1 & 1 \end{pmatrix} \cdot \begin{pmatrix} \alpha^5\\ \alpha^2\\ \alpha^3\\ \alpha \end{pmatrix} \stackrel{!}{=} \begin{pmatrix} 0\\ 0 \end{pmatrix}\hspace{0.05cm}. \]

This leads to two equations for  $\lambda_0$  and  $\lambda_1$:

\[\alpha^5 \cdot \lambda_0 + \alpha^2 \cdot \lambda_1 + \alpha^3 = 0 \hspace{0.05cm},\hspace{0.5cm}\alpha^2 \cdot \lambda_0 + \alpha^3 \cdot \lambda_1 + \alpha^1 = 0 \hspace{0.05cm}.\]

This system of equations is now clearly solvable. One gets  $\lambda_0 = \alpha^2$  and  $\lambda_1 = \alpha^6$. This means:

• The assumption that indeed  $r = 2$  positions of the received vector  $\underline {y}$  have been distorted is correct.
  
• But it is not yet known which positions have been corrupted. So much for now:
• It is not symbol positions 2 and 6, but positions 0 and 2, as shown in the following  $\text{Example 5}$  (next page).

Step (C): Localization of the error locations

After processing step  $\rm(B)$  are known:

• the number  $r$  of error locations  $e_i ≠ 0$  in the vector  $\underline {e} = (e_0, \hspace{0.05cm}\text{... }\hspace{0.05cm}, e_i, \hspace{0.05cm}\text{... }\hspace{0.05cm}, e_{n-1})$,
  

• the coefficients  $\lambda_0, \hspace{0.05cm}\text{... }\hspace{0.05cm} , \lambda_{r-1}$  of the error locator polynomial..
  
  

Now the set of error positions has to be determined:   $I_{\rm FP} = \{ i \hspace{0.1cm}| \hspace{0.1cm} e_i \ne 0,\hspace{0.1cm} 0 \le i < n \}\hspace{0.05cm}.$

There are two ways to do this (both methods are used in the following example):

• the so-called Chien search, in which one determines by inserting the possible code symbols except the zero symbol   ⇒   $(\alpha^0, \text{... }, \alpha^i, \text{... },\alpha^{n-1})$  into the error locator polynomial  its zeros,
  

• the evaluation of the equation  $\underline {L} = (L_0, \text{... }, L_i, \text{... },L_{n-1} ) = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H }}$  with the abbreviation  $L_i = {\it \Lambda}(\alpha^i)$.
  
  

$\rm GF(2^3)$ representations

$\text{Example 5:}$  In  $\text{"Example 4"}$  it was determined according to the constraints specified in  $\text{"Example 2"}$  stated boundary conditions determined that.

• $r= 2$  symbol errors are present, and
• the ELP coefficients  $\lambda_0 = \alpha^2$  and  $\lambda_1 = \alpha^6$  are.

This results in the following error locator polynomial:

\[{\it \Lambda}(x)=x \cdot \big [{\it \lambda}_0 + \lambda_1 \cdot x+x^2 \big ] =x \cdot \big [\alpha^2 + \alpha^6 \cdot x+x^2 \big ]\hspace{0.05cm}.\]

According to the Chien search one gets

\[{\it \Lambda}(\alpha^0)\hspace{0.15cm} = \hspace{0.15cm}\alpha^0 \cdot \big [ \alpha^2 + \alpha^6 \cdot 1 + 1 \big ] = \alpha^2 + (\alpha^2 + 1) + 1 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zeros} }\hspace{0.05cm},\]

\[{\it \Lambda}(\alpha^1)\hspace{0.15cm} = \hspace{0.15cm}\alpha^1 \cdot \big [\alpha^2 + \alpha^6 \cdot \alpha^1 + \alpha^2\big ]= \alpha^1 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{\rm No\hspace{0.15cm} zeros}\hspace{0.05cm},\]

\[{\it \Lambda}(\alpha^2)\hspace{0.15cm} = \hspace{0.15cm}\alpha^2 \cdot \big [ \alpha^2 + \alpha^6 \cdot \alpha^2 + \alpha^4 \big ] =\alpha^4 + \alpha^{10} + \alpha^6 = \text{...} = \hspace{0.15cm}0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm}{ \boldsymbol{\rm Zeros} }\hspace{0.05cm}.\]

Thus the two error positions with  $i = 0$  and  $i = 2$  are found   ⇒   the error vector is:   $\underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)$ .

The vector equation  $\underline {L} = \underline {\it \Lambda } \cdot { \boldsymbol{\rm H } }$  gives the same result in a more compact form:

\[\underline {L} = \underline{\it \Lambda} \cdot { \boldsymbol{\rm H } } = (\alpha^2, \alpha^6, 1, 0) \cdot \begin{pmatrix} 1 & \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4 & \alpha^5 & \alpha^6 \\ 1 & \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1 & \alpha^3 & \alpha^5 \\ 1 & \alpha^3 & \alpha^6 & \alpha^3 & \alpha^5 & \alpha^1 & \alpha^4 \\ 1 & \alpha^4 & \alpha^1 & \alpha^5 & \alpha^2 & \alpha^6 & \alpha^3 \end{pmatrix} \]

\[ \Rightarrow \hspace{0.3cm} \underline {L} = (\alpha^2,\alpha^3,\alpha^4,\alpha^5,\alpha^6,1 ,\alpha^1) + (\alpha^6,\alpha^1,\alpha^3,\alpha^5,1 ,\alpha^2,\alpha^4)+(1, \alpha^3,\alpha^6,\alpha^3,\alpha^5,\alpha^1,\alpha^4) \]

\[ \Rightarrow \hspace{0.3cm} \underline {L} = (0,\alpha^1,0,\alpha^3,\alpha^3,\alpha^5,\alpha^1)\hspace{0.3cm} \Rightarrow \hspace{0.3cm} L_0 = L_2 = 0 \hspace{0.3cm} \Rightarrow \hspace{0.3cm} \underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)\hspace{0.05cm}.\]

The example continues with the  $\text{"Example 6"}$  on the next page

.

Step (D): Final error correction

In the last step now only the  $r$  symbol errors have to be corrected, whose positions are known after completion of step  $\rm (C)$ :

• Marking the error positions in the received word  $\underline {y}$  as erasures  $\rm E$, the corresponding codeword  $\underline {z}$  can be found according to the description in chapter  "Reed-Solomon decoding at the erasure channel" .
  

• A second possibility offers the determination of the error vector  $\underline {e}$  from the equation  $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$  and correcting accordingly  $\underline {z} = \underline {y} - \underline {e} $. This procedure is the basis of the following example.
  
  

$\rm GF(2^3)$ representations

$\text{Example 6:}$  We again consider the  $\text{RSC (7, 3, 5)}_8$. In  $\text{"Example 2"}$  was.

• the received word with  $\underline{y}=\big (\alpha^3,\hspace{0.05cm} 1,\hspace{0.05cm} 0, \hspace{0.05cm}\alpha^1, \hspace{0.05cm} \alpha^2, \hspace{0.05cm} \alpha^5, \hspace{0.05cm} \alpha^5 \big)$  given, and.
• from this the syndrome  $\underline{s}=\big (\alpha^5,\hspace{0.05cm}\alpha^2, \hspace{0.05cm} \alpha^3, \hspace{0.05cm} \alpha^1\big)$  determined.

According to the calculations in  $\text{"Example 5"}$  the error vector is  $\underline {e} = (e_0, 0, e_2, 0, 0, 0, 0)$.

From  $\underline {e} \cdot \boldsymbol{\rm H }^{\rm T} = \underline {s}$  we now obtain the following governing equations for the error values  $e_0$  and  $e_2$:

\[\underline {e} \cdot \boldsymbol{\rm H }^{\rm T}= \begin{pmatrix} e_0 & 0 & e_2 & 0 & 0 & 0 & 0 \end{pmatrix}\cdot \begin{pmatrix} 1 & 1 & 1 & 1 \\ \alpha^1 & \alpha^2 & \alpha^3 & \alpha^4\\ \alpha^2 & \alpha^4 & \alpha^6 & \alpha^1\\ \alpha^3 & \alpha^6 & \alpha^2 & \alpha^{5}\\ \alpha^4 & \alpha^1 & \alpha^{5} & \alpha^{2}\\ \alpha^5 & \alpha^{3} & \alpha^{1} & \alpha^{6}\\ \alpha^6 & \alpha^{5} & \alpha^{4} & \alpha^{3} \end{pmatrix} \stackrel{!}{=} \underline {s} = \begin{pmatrix} \alpha^5 & \alpha^2 & \alpha^3 & \alpha^1 \end{pmatrix} \]

\[\Rightarrow \hspace{0.3cm}e_0 \cdot (1, 1, 1, 1) + e_2 \cdot ( \alpha^2, \alpha^4, \alpha^6, \alpha^1)\stackrel{!}{=} ( \alpha^5, \alpha^2, \alpha^3, \alpha^1)\]

\[\Rightarrow \hspace{0.3cm} e_0 + e_2 \cdot \alpha^2 = \alpha^5\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^4 = \alpha^2\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^6 = \alpha^3\hspace{0.05cm},\hspace{0.2cm} e_0 + e_2 \cdot \alpha^1 = \alpha^1\hspace{0.05cm}.\]

All equations lead to the result  $e_0 = 1$  and  $e_2 =\alpha^2$.

Thus the corrected codeword with  $\underline {y} = (\alpha^3,\hspace{0.05cm} 1,\hspace{0.05cm} 0,\hspace{0.05cm} \alpha^1,\hspace{0.05cm} \alpha^2,\hspace{0.05cm} \alpha^5,\hspace{0.05cm} \alpha^5)$  und  $\underline {e}= (1,\hspace{0.05cm} 0,\hspace{0.05cm} \alpha^2,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0,\hspace{0.05cm} 0)$:

\[\underline {z} = \underline {y} - \underline {e} = \underline {y} + \underline {e}= (\alpha^1,\hspace{0.03cm} 1,\hspace{0.03cm} \alpha^2,\hspace{0.03cm} \alpha^1,\hspace{0.03cm} \alpha^2,\hspace{0.03cm} \alpha^5,\hspace{0.03cm} \alpha^5)\hspace{0.05cm}. \]

This is a valid codeword of  $\text{RSC (7, 3, 5)}_8$.

Fast Reed-Solomon decoding

The class of Reed–Solomon codes was already introduced in 1960 by the publication  [RS60] introduced. However, their efficient decoding was not possible until a decade or two later.

In the last pages we have demonstrated the so-called Petersen algorithm including the Chien search on the example of  $\text{RSC (7, 3, 5)}_8$  which can correct up to  $t = 2$  errors. The decoding process focused on setting up and solving the key equation where the zeros of a degree $2$ polynomial in the field  $\rm GF(7)$  had to be found. It was to be recognized that already this algebraic decoding is connected with large expenditure.

For codes used in practice with large codeword length  $n$  and high correctability  $t$  the decoding effort would explode if faster decoding algorithms had not been found. For example, in the Reed–Solomon code  $\text{RSC (255, 223, 33)}_{256}$, mentioned early in the ESA/NASA standard for satellite transmission, up to  $t = 16$  zeros must be found in the field  $\rm GF(255)$  to decode a single codeword. And this in real time!

Beginning in the late 1960s, many scientists sought faster decoding algorithms for Reed–Solomon codes:

• In  "Berlekamp–Massey algorithm"  $\rm (BMA)$  the key equation  $\underline {\it \Lambda} \cdot \underline{s }^{\rm T} = 0$  represented as a feedback shift register, see for example  [Mas69],  [Fri96] und  [Bos98]. The problem is thus reduced to the synthesis of an autoregressive filter. This algorithm works much faster than the (more easily comprehensible) Petersen algorithm.
  

• Somewhat later, in  [SK+75]  A decoding method based on the  "Euclidean algorithm"  has been proposed. This provides the greatest common divisor of two integers, which is used for decoding. The Euclidean algorithm is comparably fast as the  $\rm BMA$. More detailed information can be found again in  [Bos98] and  [Fri96].
  

• Other efficient decoding methods of Reed–Solomon codes operate in the frequency domain  using the  "Discrete Fourier Transform"  $\rm (DFT)$  in the field  ${\rm GF}(n)$.
  
  

The basic features of Reed–Solomon error correction were already developed in the 1960s. But up to the present time (2013) the (as fast as possible) algebraic decoding of these codes is a highly topical field of research.

Exercises for the chapter

Exercise 2.12: Decoding at RSC (7, 4, 4) to Base 8

Exercise 2.12Z: Reed-Solomon Syndrome Calculation

Exercise 2.13: Decoding at RSC (7, 3, 5) to Base 8

Exercise 2.14: Petersen Algorithm