Betrachtetes Szenario
Wir betrachten nun abschließend den Fall, dass man ein Experiment fortlaufend durchführt und zu jedem diskreten Zeitpunkt $ν =$ 1, 2, 3, ….. ein Ereignis $E_ν$ eintritt. Hierbei soll gelten: $$E_\nu \in G = \{ E_{\rm 1}, E_{\rm 2}, \hspace{0.1cm}...\hspace{0.1cm}, E_\mu , \hspace{0.1cm}...\hspace{0.1cm}, E_M \}.$$
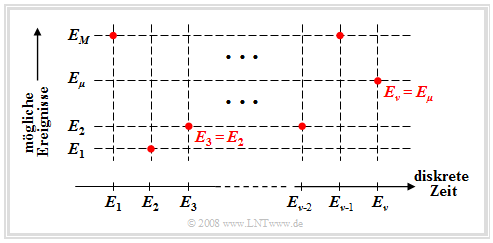
Diese mathematisch nicht ganz saubere Nomenklatur bedeutet (siehe nachfolgende Grafik):
- Die $M$ möglichen Ereignisse werden mit dem Laufindex $μ$ durchnummeriert.
- Der Index $ν$ benennt die diskreten Zeitpunkte, zu denen Entscheidungen gefällt werden.
Zur einfacheren Darstellung beschränken wir uns im Folgenden auf den Fall $M =$ 2 mit der Grundmenge $G$ = { $A, B$}. Wir berücksichtigen, dass die Wahrscheinlichkeit des Ereignisses $E_ν$ durchaus von allen vorherigen Ereignissen – also von $E_{ν–1}, E_{ν–2}, E_{ν–3}$, . . . – abhängen kann. Das bedeutet auch, dass wir eine Ereignisfolge mit inneren statistischen Bindungen betrachten.
Dieses Szenario ist ein Sonderfall eines zeit- und wertdiskreten Zufallsprozesses. Solche Prozesse werden in Kapitel 4.4 noch ausführlich behandelt.
Aus einem Kartenstapel mit 32 Karten (darunter 4 Asse) werden nacheinander Karten gezogen. Mit den Ereignissen $A =$ „die gezogene Karte ist ein Ass” und $B =$ „die gezogene Karte ist kein Ass” lauten die Wahrscheinlichkeiten zum Zeitpunkt $ν =$ 1: $${\rm Pr} (A_{\rm 1}) = \frac{4}{32}= \frac{1}{8}; \hspace{0.5cm}{\rm Pr} (B_{\rm 1}) = \frac{28}{32}= \frac{7}{8}.$$
Die Wahrscheinlichkeit Pr( $A_2$), dass zur Zeit $ν =$ 2 ein Ass gezogen wird, hängt nun davon ab,
- ob zum Zeitpunkt $ν =$ 1 ein Ass gezogen wurde ⇒ Pr( $A_2$) = 3/31 < 1/8, oder
- ob zum Zeitpunkt $ν =$ 1 kein Ass gezogen wurde ⇒ Pr( $A_2$) = 4/31 > 1/8.
Auch die Wahrscheinlichkeiten Pr( $A_ν$) zu späteren Zeitpunkten $ν$ hängen stets vom Eintreffen bzw. Nichteintreffen aller vorherigen Ereignisse $E_1 ... E_{ν–1}$ ab.
Allgemeine Definition einer Markovkette
In Sonderfällen, die allerdings sehr häufig vorkommen, kann das oben beschriebene Szenario durch eine Markovkette beschrieben werden.
Eine Markovkette $k$-ter Ordnung (englisch: Markov Chain) dient als Modell für zeit- und wertdiskrete Vorgänge, bei denen die Ereigniswahrscheinlichkeiten zur Zeit $ν$ von den vorherigen Ereignissen $E_{ν–1}, ... , E_{ν–k}$ abhängen und durch $M^{k+1}$ bedingte Wahrscheinlichkeiten ausgedrückt werden können. Für $M =$ 2 gibt es deshalb $2^{k+1}$ solcher Wahrscheinlichkeiten: $${\rm Pr} ( E_\nu \hspace {0.05cm}| \hspace {0.05cm}E_{\nu {\rm -1 }},\hspace {0.1cm} ...\hspace {0.1cm}, E_{\nu { -k }}) \hspace {0.5cm} {\rm mit}\hspace {0.5cm} E_{\nu }\in \{ A, B \}, \hspace {0.1cm}...\hspace {0.1cm}, E_{\nu { -k }} \in \{ A, B \}.$$
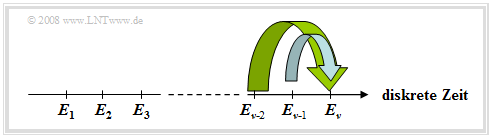
Das nachfolgende Bild verdeutlicht diesen Sachverhalt am Beispiel $k =$ 2.
Natürliche Sprachen sind oft durch Markovketten beschreibbar, wobei allerdings die Ordnung $k$ gegen Unendlich strebt. Nähert man einen Text durch eine Markovkette 2. Ordnung an, so ergibt sich zwar kein sinnvoller Inhalt, aber die Struktur der Sprache ist erkennbar.
Das untere Bild zeigt links einen Text, der ausgehend von einer deutschen Buchvorlage mit Bindungen bis zu zweiter Ordnung synthetisch erzeugt wurde. Beim rechten Text wurde eine englische Vorlage verwendet. Man erkennt trotz der Beschränkung $k =$ 2 viele (kurze) deutsche bzw. englische Wörter und auch, dass deutsche Wörter im Mittel länger sind als englische.
Markovkette erster Ordnung
Im Folgenden beschränken wir uns stets auf den Sonderfall $k =$ 1.
Bei einer Markovkette erster Ordnung (englisch: First Order Markov Chain) werden lediglich die statistische Bindung zum letzten Ereignis berücksichtigt, die in der Praxis meist auch am stärksten ist.
Eine binäre Markovkette ⇒ Grundmenge $G$ = { $A, B$ } weist folgende Wahrscheinlichkeiten auf: $${\rm Pr}(A_\nu) = {\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) ,$$ $${\rm Pr}(B_\nu) = {\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}) \cdot {\rm Pr}(A_{\nu - 1}) \hspace{0.1cm} + \hspace{0.1cm} {\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}) \cdot {\rm Pr}(B_{\nu - 1}) .$$
Hierzu ist anzumerken:
- Pr( $A_ν$) steht als Abkürzung für die Wahrscheinlichkeit, dass $E_ν = A$ ist.
- Zu jedem beliebigen Zeitpunkt $ν$ gilt: Pr( $B_ν$) = 1 – Pr( $A_ν$).
- Es gibt zu jedem Zeitpunkt vier Übergangswahrscheinlichkeiten Pr( $E_ν | E_{ν–1}$), von denen jedoch nur zwei unabhängig sind, denn es gilt:
$${\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}) = 1 - {\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}A_{\nu - 1}), \hspace{0.5cm}{\rm Pr}(A_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}) = 1 - {\rm Pr}(B_\nu \hspace{0.05cm} | \hspace{0.05cm}B_{\nu - 1}).$$
- Durch Verallgemeinerung dieser letzten Aussage gelangt man zu dem Ergebnis, dass es bei einer Markovkette mit $M$ Ereignissen zu jedem Zeitpunkt $ν$ genau $M · (M – 1)$ voneinander unabhängige Übergangswahrscheinlichkeiten gibt.
Mit den vorgegebenen Übergangswahrscheinlichkeiten Pr( $A_ν | A_{ν–1}$) = 0.2 und Pr( $B_ν | B_{ν–1}$) = 0.4 sind auch die beiden anderen Übergangswahrscheinlichkeiten festgelegt: Pr( $B_ν | A_{ν–1}$) = 0.8 und Pr( $A_ν | B_{ν–1}$) = 0.6.