Allgemeine Beschreibung und Definition
Eine Zufallsgröße $x$ bezeichnet man als gleichverteilt, wenn sie nur Werte im Bereich von $x_{\rm min}$ bis $x_{\rm max}$ annehmen kann, und zwar mit gleicher Wahrscheinlichkeit.
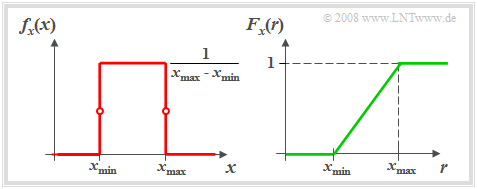
Die Grafik zeigt links die Wahrscheinlichkeitsdichtefunktion (abgekürzt WDF) und rechts die Verteilungsfunktion (kurz VTF) einer gleichverteilten Zufallsgröße $x$.
Daraus können folgende Eigenschaften abgeleitet werden:
- Die WDF $f_{\rm x}(x)$ besitzt im Bereich von $x_{\rm min}$ bis $x_{\rm max}$ den konstanten Wert $1/(x_{\rm max} - x_{\rm min})$, wobei an den beiden Bereichsgrenzen für $f_{\rm x}(x)$ jeweils nur der halbe Wert – also der Mittelwert zwischen links- und rechtsseitigem Grenzwert – zu setzen ist.
- Die Verteilungsfunktion $F_{\rm x}(r)$ steigt im Bereich von $x_{\rm min}$ bis $x_{\rm max}$ linear von 0 auf 1 an.
- Mittelwert und Streuung haben bei der Gleichverteilung die folgenden Werte:
$$m_{\rm 1} = \frac{\it x_ {\rm max} + \it x_{\rm min}}{2},\hspace{0.5cm} \sigma = \frac{\it x_{\rm max} - \it x_{\rm min}}{2 \sqrt{3}}.$$
- Bei symmetrischer WDF $(x_{\rm min} = –x_{\rm max})$ erhält man als Sonderfall $m_1 =$ 0 und $σ^2 = x_{\rm max}^2/3.$
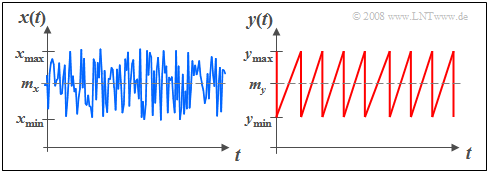
Hier sehen Sie zwei Signalverläufe mit gleichförmiger Amplitudenverteilung.
- Links ist statistische Unabhängigkeit der einzelnen Abtastwerte vorausgesetzt, das heißt, $x_ν$ kann alle Werte zwischen $x_{\rm min}$ und $x_{\rm max}$ mit gleicher Wahrscheinlichkeit annehmen, und zwar unabhängig von der Vergangenheit $(x_{ν–1}, x_{ν–2}, ...).$
- Beim rechten Signal $y(t)$ ist diese Unabhängigkeit aufeinanderfolgender Signalwerte nicht mehr gegeben. Vielmehr stellt dieses Sägezahnsignal ein deterministisches Signal dar.