Rayleighverteilung
Diese Verteilung spielt für die Beschreibung zeitvarianter Kanäle – wie sie beispielweise im Mobilfunk vorliegen – eine zentrale Rolle. So weist nichtfrequenzselektives Fading eine solche Verteilung auf, wenn zwischen der festen Basisstation und dem mobilen Teilnehmer keine Sichtverbindung besteht.
Die Rayleighverteilung besitzt folgende charakteristische Eigenschaften:
- Eine rayleighverteilte Zufallsgröße $x$ kann keine negativen Werte annehmen und der theoretisch mögliche Wert $x =$ 0 tritt auch nur mit der Wahrscheinlichkeit 0 auf.
- Für $x$ ≥ 0 hat die WDF mit dem Verteilungsparameter $λ$ den folgenden Verlauf:
$$f_{\rm x}(x)=\frac{x}{\lambda^2}\cdot\rm e^{-{\it x^{\rm 2}} /{(\rm 2 \it \lambda^{\rm 2})}}.$$
- Das $k$-te Moment einer rayleighverteilten Zufallsgröße $x$ ergibt sich allgemein zu
$$m_k=(2\cdot \lambda^{\rm 2})^{\it k/\rm 2}\cdot {\rm \Gamma}( 1+ \frac{\it k}{\rm 2}) \hspace{0.3cm}{\rm mit }\hspace{0.3cm}{\rm \Gamma}(x)= \int_{0}^{\infty} t^{x-1} \cdot {\rm e}^{-t} \hspace{0.1cm}{\rm d}t.$$
- Daraus lassen sich Mittelwert und Streuung folgendermaßen berechnen:
$$m_1=\sqrt{2}\cdot \lambda\cdot {\rm \Gamma}(1.5) = \sqrt{2}\cdot \lambda\cdot {\sqrt{\pi}}/{2} =\lambda\cdot\sqrt{{\pi}/{2}},$$ $$m_2=2 \lambda^2 \cdot {\rm \Gamma}(2) = 2 \lambda^2 \hspace{0.3cm}\Rightarrow \hspace{0.3cm}\sigma = \sqrt{m_2 - m_1^2} =\lambda\cdot\sqrt{2-{\pi}/{2}}.$$
- Zur Modellierung einer rayleighverteilten Zufallsgröße $x$ verwendet man zum Beispiel zwei gaußverteilte, mittelwertfreie und statistisch unabhängige Zufallsgrößen $u$ und $υ$, die beide die Streuung $σ = λ$ aufweisen. Die Größen $u$ und $υ$ werden dann wie folgt verknüpft:
$$x=\sqrt{u^2+\upsilon^2}.$$
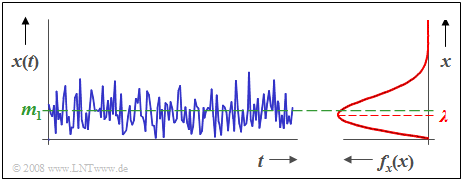
Die Grafik zeigt den Zeitverlauf $x(t)$ einer rayleighverteilten Zufallsgröße sowie die zugehörige Dichtefunktion $f_{\rm x}(x)$. Man erkennt aus dieser Darstellung:
- Die Rayleigh-WDF ist stets unsymmetrisch.
- Der Mittelwert $m_1$ liegt etwa 25% oberhalb des WDF-Maximums, das bei $x = λ$ auftritt.