Exercise 4.11Z: Code Rate from the Parity-check Matrix
In this exercise, the code rates of the codes $\mathcal {C}_1, \, \mathcal {C}_2, \, \mathcal {C}_3$ and $\mathcal {C}_4$ are to be determined, where the codes are given by their test matrices alone. A lower bound on the code rate $R$ reads:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} \hspace{0.05cm}.$$
If the $m$ parity-check equations of all matrix–rows are linearly independent, then the equal sign in the above inequality holds.
Used here is the following nomenclature:
- $w_{\rm Z}(j)$ with $1 ≤ j ≤ m$ being the "Hamming weight" of $j$th row of the parity-check matrix.
- By expectation value formation results:
- $${\rm E}[w_{\rm Z}] =\frac{1}{m} \cdot \sum_{j = 1}^{m} w_{\rm Z}(j)\hspace{0.05cm}.$$
- Accordingly, $w_{\rm S}(i)$ with $1 ≤ i ≤ n$ gives the Hamming weight of $i$th column of $\mathbf{H}$ with expected value
- $${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{i = 1}^{n} w_{\rm S}(i)\hspace{0.05cm}.$$
Hints:
- This exercise belongs to the chapter "Basics of Low–density Parity–check Code "s.
- Reference is made in particular to the page "Some characteristics of LDPC codes".
Questions
Solution
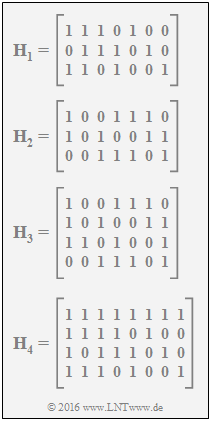
- This is the characteristic of a systematic code with $\underline{m = 3}$ parity-check equations.
- The code length is $\underline{n = 7}$.
- Thus, a codeword contains $\underline{k = 4}$ information bits.
Note: This is the "systematic (7, 4, 3)–Hamming code".
(2) The code rate of the (7, 4, 3)–Hamming–code is $\underline{R = 4/7 = 0.571}$.
- The Hamming weight for all $m = 3$ rows is $w_{\rm Z} = 4$ and for the mean Hamming–weight over all columns holds:
- $${\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n} w_{\rm S}(j) = 1/7 \cdot [2 + 3 + 2+2 + 1+1 +1] = 12/7 \hspace{0.05cm}.$$
- This applies to the specified lower bound of the code rate:
- $$R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{w_{\rm Z}} = 1 - \frac{12/7}{4}\hspace{0.15cm} \underline{= 4/7 \approx 0.571}\hspace{0.05cm}.$$
- This means: the actual code rate is equal to the lower bound ⇒ the $m = 3$ parity-check equations of $\mathbf{H}_1$ are linearly independent.
(3) The first row of $\mathbf{H}_2$ is the sum of the first row $(z_1)$ and the second row $(z_2)$ of $\mathbf{H}_1$.
- The second row is equal to $z_2 + z_3$ and the third row is $z_1 + z_3$.
- This is the identical code ⇒ rate $\underline{R = 4/7 = 0.571}$.
- Further, $w_{\rm Z} = 4$ and ${\rm E}[w_{\rm S}] = 1/7 \cdot [0 + 6 \cdot 2] = 12/7$.
(4) For this code with $n = 7$ (column count) and $m = 4$ (row count) holds:
- $$w_{\rm Z} = 4\hspace{0.05cm},\hspace{0.3cm} {\rm E}[w_{\rm S}] =\frac{1}{n} \cdot \sum_{j = 1}^{ n}w_{\rm S}(j) = 1/7 \cdot [3 + 1 + 2 +3+2 + 2+3] = 16/7\hspace{0.3cm} \Rightarrow \hspace{0.3cm} R \ge 1 - \frac{16/7}{4}= 3/7 \hspace{0.05cm}.$$
The equal sign would only apply to linearly independent parity-check equations, which is not the case here:
- The third row of $\mathbf{H}_3$ was taken from $\mathbf{H}_1$.
- If one deletes this row, $\mathbf{H}_3 = \mathbf{H}_2$ and therefore also holds: $\ \underline{R = 4/7 = 0.571}$.
(5) Here $n = 7$ and $m = 4$, as well as
- $${\rm E}[w_{\rm S}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/8 \cdot [4 + 3 + 4 + 3 + 3+2 + 2+2] = 23/8\hspace{0.05cm},\hspace{0.8cm} {\rm E}[w_{\rm Z}] \hspace{-0.15cm} \ = \ \hspace{-0.15cm}1/4 \cdot [8 + 5 + 5+5] = 23/4$$
- $$\Rightarrow \hspace{0.3cm}R \ge 1 - \frac{{\rm E}[w_{\rm S}]}{{\rm E}[w_{\rm Z}]} = 1 - \frac{23/8}{23/4} = 1/2 \hspace{0.05cm}.$$
- Since all four equations are linearly independent, the code rate is equal to the lower bound: $\underline{R = 1/2}$.
Hint: This is the "extended (8, 4, 4) Hamming code".