Exercise 4.13: Decoding LDPC Codes

Given LDPC parity-check matrix

The exercise deals with "Iterative decoding of LDPC–codes" according to the Message passing algorithm.

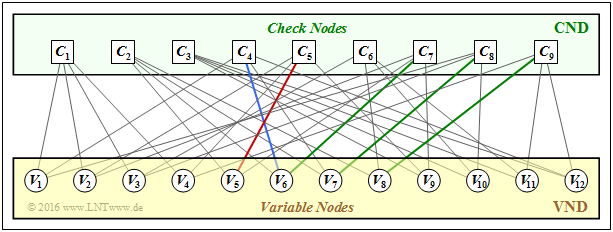
The starting point is the presented $9 × 12$ parity-check matrix $\mathbf{H}$, which is to be represented as Tanner graph at the beginning of the exercise. It should be noted:

The "variable nodes" $V_i$ denote the $n$ bits of the code word.
The "check nodes" $C_j$ represent the $m$ parity-check equations.
A connection between $V_i$ and $C_j$ indicates that the element of matrix $\mathbf{H}$ $($in row $j$, column $i)$ is $h_{j,\hspace{0.05cm} i} =1$.
For $h_{j,\hspace{0.05cm}i} = 0$ there is no connection between $V_i$ and $C_j$.
The "neighbors $N(V_i)$ of $V_i$" is called the set of all check nodes $C_j$ connected to $V_i$ in the Tanner graph.
Correspondingly, to $N(C_j)$ belong all variable nodes $V_i$ with a connection to $C_j$.

The decoding is performed alternately with respect to

the variable nodes ⇒ "variable nodes decoder" $\rm (VND)$, and

the check nodes ⇒ "check nodes decoder" $\rm (CND)$.

This is referred to in subtasks (5) and (6).

Hints:

The exercise belongs to the chapter "Basic information about Low–density Parity–check Codes".

Reference is made in particular to the section "Iterative decoding of LDPC codes".

Questions

Solution

(1) The variable node$\rm (VN)$ $V_i$ stands for the $i$th code word bit, so that $I_{\rm VN}$ is equal to the code word length $n$.

From the column number of the $\mathbf{H}$–matrix, we can see $I_{\rm VN} = n \ \underline{= 12}$.
For the set of all variable nodes,one can thus write in general: ${\rm VN} = \{V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , V_i, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ V_n\}$.
The check node ${\rm (CN)} \ C_j$ represents the $j$ parity-check equation, and for the set of all check nodes, ${\rm CN} = \{C_1, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_j, \hspace{0.05cm} \text{...} \hspace{0.05cm} , \ C_m\}$.
From the number of rows of the $\mathbf{H}$ matrix we get $I_{\rm CN} \ \underline {= m = 9}$.

(2) The results can be read from the Tanner graph sketched below.

Tanner graph for the present example.

Correct are the proposed solutions 1, 2 and 5:

The matrix element $h_{5,\hspace{0.05cm}5}$ (column 5, row 5) ist $1$
⇒ red edge.
The matrix element $h_{4,\hspace{0.05cm} 6}$ (column 4, row 6) ist $1$
⇒ blue edge.
The matrix element $h_{6, \hspace{0.05cm}4}$ (column 6, row 4) ist $0$
⇒ no edge.
$h_{6,\hspace{0.05cm} 10} = h_{6,\hspace{0.05cm} 11} = 1$. But $h_{6,\hspace{0.05cm}12} = 0$
⇒ not all three edges exist.
It holds $h_{7,\hspace{0.05cm}6} = h_{8,\hspace{0.05cm}7} = h_{9,\hspace{0.05cm}8} = 1$ ⇒ green edges.

(3) It is a regular LDPC code with

$w_{\rm Z}(j) = 4 = w_{\rm Z}$ für $1 ≤ j ≤ 9$,
$w_{\rm S}(i) = 3 = w_{\rm S}$ für $1 ≤ i ≤ 12$.

The answers 2 and 3 are correct, as can be seen from the first row and ninth column, respectively, of the parity-check matrix $\mathbf{H}$.
The Tanner graph confirms these results:

From $C_1$ there are edges to $V_1, \ V_2, \ V_3$, and $V_4$.
From $V_9$ there are edges to $C_3, \ C_5$, and $C_7$.

The answers 1 and 4 cannot be correct already because

the neighborhood $N(V_i)$ of each variable node $V_i$ contains exactly $w_{\rm S} = 3$ elements, and
the neighborhood $N(C_j)$ of each check ndes $C_j$ contains exactly $w_{\rm Z} = 4$ elements.

(4) Correct are proposed solutions 1 and 2, as can be seen from the "corresponding theory page":

At the beginning of decoding $($so to speak at iteration $I=0)$ the $L$–values of the variable nodes ⇒ $L(V_i)$ are preallocated with the channel input values.
Later $($from iteration $I = 1)$ the log–likelihood–ratio $L(C_j → V_i)$ transmitted by the CND is considered in the VND as a priori information.
Answer 3 is wrong. Rather, the correct answer would be: there are analogies between the VND algorithm and the decoding of a repetition code.

(5) Correct is only proposed solution 3 because.

the final a posteriori $L$ values are derived from the VND, not from the CND,
the $L$ value $L(C_j → V_i)$ represents extrinsic information for the CND, and
there are indeed analogies between the CND–algorithm and SPC–decoding.

	$C_4$ and $V_6$.
	$C_5$ and $V_5$.
	$C_6$ and $V_4$.
	$C_6$ and $V_i$ for $i > 9$.
	$C_j$ and $V_{j-1}$ for $j > 6$.

	$N(V_1) = \{C_1, \ C_2, \ C_3, \ C_4\}$,
	$N(C_1) = \{V_1, \ V_2, \ V_3, \ V_4\}$,
	$N(V_9) = \{C_3, \ C_5, \, C_7\}$,
	$N(C_9) = \{V_3, \ V_5, \ V_7\}$.

	At the beginning $($iteration 0$)$ the $L$–values of the nodes $V_1, \hspace{0.05cm} \text{...} \hspace{0.05cm}, \ V_n$ are preassigned corresponding to the channel input values $y_i$.
	For the VND represents $L(C_j → V_i)$ a-priori information.
	There are analogies between the "variable node decoder" and the decoding of a single parity–check code.

	The CND returns at the end the desired a-posteriori $L$–values.
	For the CND represents $L(C_j → V_i)$ a-priori information.
	There are analogies between the "check node decoder" and the decoding of a single parity–check code.