Complementary Gaussian Error Functions

Open Applet in new Tab   Deutsche Version Öffnen

Applet Description

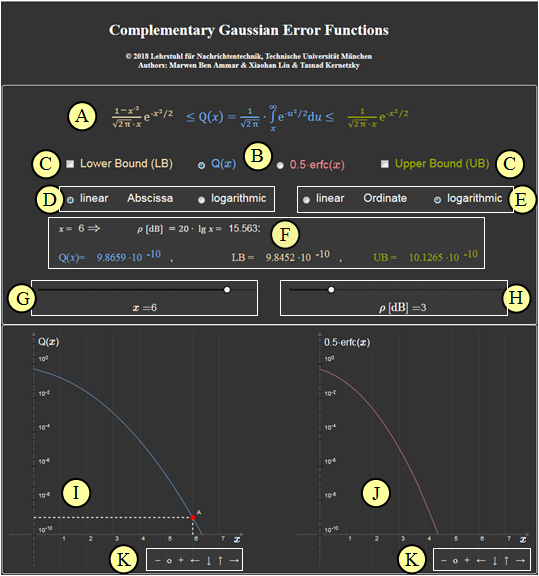
This applet allows the calculation and graphical representation of the (complementary) Gaussian error functions  ${\rm Q}(x)$  and  $1/2\cdot {\rm erfc}(x)$, which are of great importance for error probability calculation.

• Both the abscissa and the function value can be represented either linearly or logarithmically.
• For both functions an upper bound  $\rm (UB)$  and a lower bound  $\rm (LB)$  are given.

Theoretical Background

In the study of digital transmission systems, it is often necessary to determine the probability that a (mean-free) Gaussian distributed random variable  $x$  with variance  $σ^2$  exceeds a given value  $x_0$.  For this probability holds:

$${\rm Pr}(x > x_0)={\rm Q}(\frac{x_0}{\sigma}) = 1/2 \cdot {\rm erfc}(\frac{x_0}{\sqrt{2} \cdot \sigma}).$$

The function ${\rm Q}(x )$

The function  ${\rm Q}(x)$  is called the  complementary Gaussian error integral.  The following calculation rule applies:

$${\rm Q}(x ) = \frac{1}{\sqrt{2\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}/\hspace{0.05cm} 2}\,{\rm d} u .$$

• This integral cannot be solved analytically and must be taken from tables if one does not have this applet available.
• Specially for larger  $x$  values  (i.e., for small error probabilities), the bounds given below provide a useful estimate for  ${\rm Q}(x)$, which can also be calculated without tables.
• An upper bound  $\rm (UB)$  of this function is:

$${\rm Q}_{\rm UB}(x )=\text{Upper Bound }\big [{\rm Q}(x ) \big ] = \frac{ 1}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{- x^{2}/\hspace{0.05cm}2} > {\rm Q}(x).$$

• Correspondingly, for the lower bound  $\rm (LB)$:

$${\rm Q}_{\rm LB}(x )=\text{Lower Bound }\big [{\rm Q}(x ) \big ] =\frac{1-1/x^2}{\sqrt{2\pi}\cdot x}\cdot {\rm e}^{-x^ 2/\hspace{0.05cm}2} ={\rm Q}_{\rm UB}(x ) \cdot (1-1/x^2)< {\rm Q}(x).$$

However, in many program libraries, the function  ${\rm Q}(x )$  cannot be found.

The function $1/2 \cdot {\rm erfc}(x )$

On the other hand, in almost all program libraries, you can find the  Complementary Gaussian Error Function:

$${\rm erfc}(x) = \frac{2}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u ,$$

which is related to  ${\rm Q}(x)$  as follows:   ${\rm Q}(x)=1/2\cdot {\rm erfc}(x/{\sqrt{2}}).$

• Since in almost all applications this function is used with the factor  $1/2$, in this applet exactly this function was realized:

$$1/2 \cdot{\rm erfc}(x) = \frac{1}{\sqrt{\pi}}\int_{x}^{ +\infty}\hspace{-0.2cm}{\rm e}^{-u^{2}}\,{\rm d} u .$$

• Once again, an upper and lower bound can be specified for this function:

$$\text{Upper Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ 1}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} ,$$

$$\text{Lower Bound }\big [1/2 \cdot{\rm erfc}(x) \big ] = \frac{ {1-1/(2x^2)}}{\sqrt{\pi}\cdot 2x}\cdot {\rm e}^{- x^{2}} .$$

When which function offers advantages?

$\text{Example 1:}$  We consider binary baseband transmission. Here, the bit error probability  $p_{\rm B} = {\rm Q}({s_0}/{\sigma_d})$, where the useful signal can take the values  $\pm s_0$  and the noise root mean square value  $\sigma_d$ .

It is assumed that tables are available listing the argument of the two Gaussian error functions at distance  $0.1$.  With  $s_0/\sigma_d = 4$  one obtains for the bit error probability according to the function  ${\rm Q}(x )$:

$$p_{\rm B} = {\rm Q} (4) \approx 0.317 \cdot 10^{-4}\hspace{0.05cm}.$$

According to the second equation, we get:

$$p_{\rm B} = {1}/{2} \cdot {\rm erfc} ( {4}/{\sqrt{2} })= {1}/{2} \cdot {\rm erfc} ( 2.828)\approx {1}/{2} \cdot {\rm erfc} ( 2.8)= 0.375 \cdot 10^{-4}\hspace{0.05cm}.$$

• The first value is more correct.  In the second method of calculation, one must round or – even better – interpolate, which is very difficult due to the strong nonlinearity of this function.
  
• Accordingly, with the given numerical values, ${\rm Q}(x )$  is more suitable.  However, outside of exercise examples  $s_0/\sigma_d$  will usually have a "curvilinear" value.  In this case, of course,  ${\rm Q}(x)$  offers no advantage over  $1/2 \cdot{\rm erfc}(x)$.

$\text{Example 2:}$  With the energy per bit  $(E_{\rm B})$  and the noise power density  $(N_0)$  the bit error probability of Binary Phase Shift Keying  (BPSK) is:

$$p_{\rm B} = {\rm Q} \left ( \sqrt{ {2 E_{\rm B} }/{N_0} }\right ) = {1}/{2} \cdot { \rm erfc} \left ( \sqrt{ {E_{\rm B} }/{N_0} }\right ) \hspace{0.05cm}.$$

For the numerical values  $E_{\rm B} = 16 \rm mWs$  and  $N_0 = 1 \rm mW/Hz$  we obtain:

$$p_{\rm B} = {\rm Q} \left (4 \cdot \sqrt{ 2} \right ) = {1}/{2} \cdot {\rm erfc} \left ( 4\right ) \hspace{0.05cm}.$$

• The first way leads to the result  $p_{\rm B} = {\rm Q} (5.657) \approx {\rm Q} (5.7) = 0.6 \cdot 10^{-8}\hspace{0.01cm}$, while   $1/2 \cdot{\rm erfc}(x)$  here the more correct value  $p_{\rm B} \approx 0.771 \cdot 10^{-8}$  yields.
• As in the first example, however, you can see:   The functions  ${\rm Q}(x)$  and  $1/2 \cdot{\rm erfc}(x)$  are basically equally well suited.
• Advantages or disadvantages of one or the other function arise only for concrete numerical values.

Exercises

• First select the number  $(1, 2, \text{...})$  of the exercise.  The number  $0$  corresponds to a "Reset":  Same setting as at program start.
• A task description is displayed.  The parameter values ​​are adjusted.  Solution after pressing "Show solution".
  

(1)   Find the values of the function  ${\rm Q}(x)$  for  $x=1$,  $x=2$,  $x=4$  and  $x=6$.  Interpret the graphs for linear and logarithmic ordinates.

• The applet returns the values  ${\rm Q}(1)=1.5866 \cdot 10^{-1}$,  ${\rm Q}(2)=2. 275 \cdot 10^{-2}$,  ${\rm Q}(4)=3.1671 \cdot 10^{-5}$  and  ${\rm Q}(6)=9.8659 \cdot 10^{-10}$.
• With linear ordinate, the values for  $x>3$  are indistinguishable from the zero line.  More interesting is the plot with logarithmic ordinate.

(2)   Evaluate the two bounds  ${\rm UB}(x )=\text{Upper Bound }\big [{\rm Q}(x ) \big ]$  and  ${\rm LB}(x )=\text{Lower Bound }\big [{\rm Q}(x ) \big ]$  for the  ${\rm Q}$  function.

• For  $x \ge 2$  the upper bound is only slightly above  ${\rm Q}(x)$  and the lower bound is only slightly below  ${\rm Q}(x)$. 
• For example:  ${\rm Q}(x=4)=3.1671 \cdot 10^{-5}$   ⇒   ${\rm LB}(x=4)=3.1366 \cdot 10^{-5}$,   ${\rm UB}(x=4)=3.3458 \cdot 10^{-5}$.
• The upper bound has greater significance for assessing a communications system than "LB",  since this corresponds to a "worst case" consideration.

(3)   Try to use the app to determine  ${\rm Q}(x=2 \cdot \sqrt{2} \approx 2.828)$  as accurately as possible despite the quantization of the input parameter.

• The program returns for  $x=2.8$  the too large result  $2.5551 \cdot 10^{-3}$  and for  $x=2.85$  the result  $2.186 \cdot 10^{-3}$.  The exact value lies in between.
• But it also holds:  ${\rm Q}(x=2 \cdot \sqrt{2})=0.5 \cdot {\rm erfc}(x=2)$.  This gives the exact value  ${\rm Q}(x=2 \cdot \sqrt{2})=2.3389 \cdot 10^{-3}$.

(4)   Find the values of the function  $0.5 \cdot {\rm erfc}(x)$  for  $x=1$,  $x=2$,  $x=3$  and  $x=4$.  Interpret the exact results and the bounds.

• The applet returns:  $0.5 \cdot {\rm erfc}(1)=7.865 \cdot 10^{-2}$,  $0.5 \cdot {\rm erfc}(2)=2. 3389 \cdot 10^{-3}$,  $0.5 \cdot {\rm erfc}(3)=1.1045 \cdot 10^{-5}$  and  $0.5 \cdot {\rm erfc}(4)=7.7086 \cdot 10^{-9}$.
• All the above statements about  ${\rm Q}(x)$  with respect to suitable representation type and upper and lower bounds also apply to the function  $0.5 \cdot {\rm erfc}(x)$.

(5)   The results of  (4)  are now to be converted for the case of a logarithmic abscissa.  The conversion is done according to  $\rho\big[{\rm dB}\big ] = 20 \cdot \lg(x)$.

• The linear abscissa value  $x=1$  leads to the logarithmic abscissa value  $\rho=0\ \rm dB$   ⇒   $0. 5 \cdot {\rm erfc}(\rho=0\ {\rm dB})={0.5 \cdot \rm erfc}(x=1)=7.865 \cdot 10^{-2}$.
• Similarly  $0.5 \cdot {\rm erfc}(\rho=6.021\ {\rm dB}) =0.5 \cdot {\rm erfc}(x=2)=2. 3389 \cdot 10^{-3}$,     $0.5 \cdot {\rm erfc}(\rho=9.542\ {\rm dB})=0.5 \cdot {\rm erfc}(3)=1.1045 \cdot 10^{-5}$,   
• $0.5 \cdot {\rm erfc}(\rho=12.041\ {\rm dB})= 0.5 \cdot {\rm erfc}(4)=7.7086 \cdot 10^{-9}$.
• As per right diagram:  $0.5 \cdot {\rm erfc}(\rho=6\ {\rm dB}) =2.3883 \cdot 10^{-3}$,     $0.5 \cdot {\rm erfc}(\rho=9. 5\ {\rm dB}) =1.2109 \cdot 10^{-5}$,     $0.5 \cdot {\rm erfc}(\rho=12\ {\rm dB}) =9.006 \cdot 10^{-9}$.

(6)   Find  ${\rm Q}(\rho=0\ {\rm dB})$,  ${\rm Q}(\rho=5\ {\rm dB})$  and  ${\rm Q}(\rho=10\ {\rm dB})$,  and establish the relationship between linear and logarithmic abscissa.

• The program returns for logarithmic abscissa  ${\rm Q}(\rho=0\ {\rm dB})=1. 5866 \cdot 10^{-1}$,  ${\rm Q}(\rho=5\ {\rm dB})=3.7679 \cdot 10^{-2}$,  ${\rm Q}(\rho=10\ {\rm dB})=7.827 \cdot 10^{-4}$.
• The conversion is done according to the equation  $x=10^{\hspace{0.05cm}0.05\hspace{0.05cm} \cdot\hspace{0.05cm} \rho[{\rm dB}]}$.  For  $\rho=0\ {\rm dB}$  we get  $x=1$   ⇒   ${\rm Q}(\rho=0\ {\rm dB})={\rm Q}(x=1) =1.5866 \cdot 10^{-1}$.
• For  $\rho=5\ {\rm dB}$  we get  $x=1.1778$   ⇒   ${\rm Q}(\rho=5\ {\rm dB})={\rm Q}(x=1. 778) =3.7679 \cdot 10^{-2}$.  From the left diagram:  ${\rm Q}(x=1.8) =3.593 \cdot 10^{-2}$.
• For  $\rho=10\ {\rm dB}$  we get  $x=3.162$   ⇒   ${\rm Q}(\rho=10\ {\rm dB})={\rm Q}(x=3. 162) =7.827 \cdot 10^{-4}$.  After "quantization":  ${\rm Q}(x=3.15) =8.1635 \cdot 10^{-4}$.

Applet Manual

    (A)     Verwendete Gleichungen am Beispiel  ${\rm Q}(x)$

    (B)     Auswahloption für  ${\rm Q}(x)$  oder  ${\rm 0.5 \cdot erfc}(x)$

    (C)     Schranken  ${\rm LB}$  und  ${\rm UB}$  werden gezeichnet

    (D)     Auswahl, ob Abszisse linear  $\rm (lin)$  oder logarithmisch  $\rm (log)$ 

    (E)     Auswahl, ob Ordinate linear  $\rm (lin)$  oder logarithmisch  $\rm (log)$ 

    (F)     Numerikausgabe am Beispiel  ${\rm Q}(x)$  bei linearer Abszisse

    (G)     Slidereingabe des Abszissenwertes  $x$  für lineare Abszisse

    (H)     Slidereingabe des Abszissenwertes  $\rho \ \rm [dB]$  für logarithmische Abszisse

    (I)     Grafikausgabe der Funktion  ${\rm Q}(x)$  – hier:  lineare Abszisse

    (J)     Grafikausgabe der Funktion  ${\rm 0.5 \cdot erfc}(x)$  – hier:  lineare Abszisse

    (K)     Variationsmöglichkeit für die graphischen Darstellungen

$\hspace{1.5cm}$"$+$" (Vergrößern),

$\hspace{1.5cm}$ "$-$" (Verkleinern)

$\hspace{1.5cm}$ "$\rm o$" (Zurücksetzen)

$\hspace{1.5cm}$ "$\leftarrow$" (Verschieben nach links), usw.

About the Authors

This interactive calculation tool was designed and implemented at the  Institute for Communications Engineering  at the  Technical University of Munich.

• The first version was created in 2007 by  Thomas Großer  as part of his diploma thesis with “FlashMX – Actionscript” (Supervisor: Günter Söder).
• In 2018 the program was redesigned by  Xiaohan Liu  as part of her bachelor thesis  (Supervisor: Tasnád Kernetzky ) via "HTML5".
• Last revision and English version 2021 by  Carolin Mirschina  in the context of a working student activity. 

The conversion of this applet to HTML 5 was financially supported by  "Studienzuschüsse"  (Faculty EI of the TU Munich).  We thank.

Once again: Open Applet in new Tab

Open Applet in new Tab   Deutsche Version Öffnen