Gemeinsamkeiten zwischen Phasen– und Frequenzmodulation (1)
Schon im Kapitel 1.3 wurde darauf hingewiesen, dass es zwischen der Phasenmodulation (PM) und der Frequenzmodulation (FM) – siehe Kapitel 3.2 – substanzielle Gemeinsamkeiten gibt. Man fasst deshalb diese beiden verwandten Modulationsverfahren unter dem Oberbegriff „Winkelmodulation” zusammen.
Eine Winkelmodulation – abgekürzt WM – liegt dann vor, wenn sich das modulierte Signal wie folgt darstellen lässt: $$s(t) = A_{\rm T} \cdot \cos(\psi(t)) = A_{\rm T} \cdot \cos( \omega_{\rm T} \cdot t + \phi(t)) \hspace{0.05cm}.$$ Hierbei bezeichnet $A_{\rm T}$ wie bei der Amplitudenmodulation die Amplitude des Trägersignals $z(t)$. Die gesamte Information über das Quellensignal $q(t)$ steckt nun aber in der Winkelfunktion $ψ(t)$.
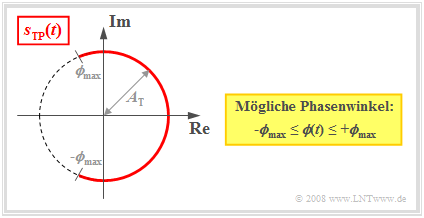
Anhand der Ortskurve – der Darstellung des äquivalenten TP–Signals $s_{\rm TP}(t)$ in der komplexen Ebene – sind folgende Charakteristika der Winkelmodulation zu erkennen (siehe Grafik am Ende des Abschnitts):
- Die Ortskurve ist ein Kreisbogen mit dem Radius $A_{\rm T}$. Daraus folgt, dass die Hüllkurve eines winkelmodulierten Signals stets konstant ist:
$$a(t) = |s_{\rm TP}(t)|= A_{\rm T}= {\rm const.}$$
- Das äquivalente TP–Signal ist bei Winkelmodulation immer komplex und durch eine zeitabhängige Phasenfunktion ${\mathbf ϕ}(t)$ (in Radian) festgelegt, welche die Nulldurchgänge von $s(t)$ bestimmt:
$$s_{\rm TP}(t)= A_{\rm T} \cdot {\rm e}^{\hspace{0.05cm}{\rm j}\hspace{0.05cm}\cdot \hspace{0.05cm}\phi(t)}\hspace{0.05cm}.$$
- Bei symmetrischem Quellensignal $q(t)$ kann ${\mathbf ϕ}(t)$ alle Werte zwischen $±ϕ_{\rm max}$ annehmen, wobei $ϕ_{\rm max}$ den Phasenhub angibt. Je größer der Phasenhub ist, desto intensiver ist die Modulation.
- Bei einer harmonischen Schwingung ist der Phasenhub $ϕ_{\rm max}$ gleich dem Modulationsindex $η$. Die Verwendung von $η$ zeigt im Folgenden also an, dass $q(t)$ nur eine einzige Frequenz beinhaltet.
- Der Zusammenhang zwischen Quellensignal $q(t)$ und Winkelfunktion $ψ(t) = \cos(ω{\rm T} · t + {\mathbf ϕ}(t))$ bzw. der daraus ableitbaren Phasenfunktion ${\mathbf ϕ}(t)$ unterscheidet sich bei der Phasen– und der Frequenzmodulation grundsätzlich, worauf im Kapitel 3.2 noch ausführlich eingegangen wird.