Exercise 1.7: Ternary Markov Chain
From LNTwww
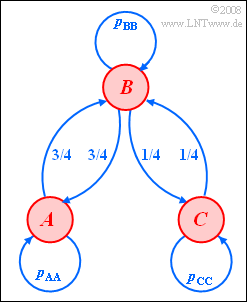
Wir betrachten eine Markovkette mit den drei möglichen Ereignissen $A, B, C$. Die Übergangswahrscheinlichkeiten sind der Grafik zu entnehmen. Ein Übergang von $A$ nach $C$ und umgekehrt ist somit nicht möglich:
$p_\text{AC} = p_\text{CA} = 0 $ .
Die drei Ereigniswahrscheinlichkeiten zum Startzeitpunkt $ν = 0$ sind wie folgt gegeben:
$Pr(A_0) = 0,$
$Pr(B_0) = 1,$
$Pr(C_0) = 0.$
Hinweis: Die Aufgabe bezieht sich auf den Abschnitt Matrix-Vektordarstellung im Kapitel 1.4
Fragebogen
Musterlösung
1.
2.
3.
4.
5.
6.
7.