Exercise 1.3Z: Winning with Roulette?

• Return to book

Beim Roulette wird bei jedem Spiel mittels einer Kugel und einer Roulettescheibe eine Gewinnzahl Z ermittelt, wobei wir davon ausgehen wollen, dass alle möglichen Zahlen Z ∈ {0, 1, 2, ..... 36} gleichwahrscheinlich sind.

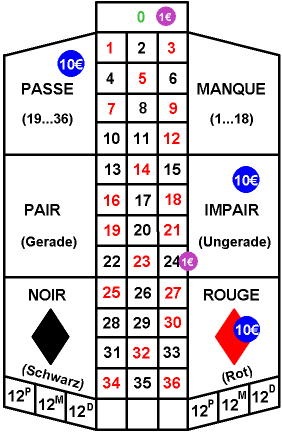
Die Mitspieler können nun mit unterschiedlich wertvollen Chips auf eine einzelne Zahl oder auf eine Zahlengruppe setzen. Einige der Möglichkeiten und die dazugehörigen Gewinne sollen hier kurz anhand der von einem Spieler gesetzten Chips erläutert werden (siehe Grafik):

• Setzt ein Spieler auf eine Zahl (im Beispiel der Chip auf „0“), so bekäme er außer seinem Einsatz als Gewinn das 35-fache zurück.

• Setzt ein Spieler auf eine Zahlengruppe mit drei Feldern (im Beispiel der Euro-Chip für die Zahlen von „22“ bis „24“), so bekäme er außer seinem Einsatz noch den 11-fachen Einsatz als Gewinn ausbezahlt.

• Setzt ein Spieler auf eine Zahlengruppe mit 18 Feldern (beispielsweise die 10 Euro-Chips auf „Rot“, auf „Impair“ und auf „Passe“), so erhält er außer seinem Einsatz als Gewinn nochmals den gleichen Betrag zurück. Gehört die gezogene Zahl nicht zu einer der von ihm besetzten Felder, so ist sein Einsatz natürlich verloren.

Hinweis: Diese Aufgabe bezieht sich auf den Lehrstoff von Kapitel 1.2. Eine Zusammenfassung der theoretischen Grundlagen mit Beispielen bringt das nachfolgende Lernvideo:

Fragebogen

1

Ein Spieler setzt gleichzeitig je einen 1 Euro-Chip auf die Felder „0“, „Rot“ und „Schwarz“. Wie groß ist sein mittlerer Gewinn pro Spiel? Hinweis: Eventuelle Verluste als negative Gewinne eingeben.

$G_a$ =

2

Wieviel gewinnt er im Mittel pro Spiel, wenn er stets je 1 Euro auf „Rot“ und „Schwarz“ setzt?

$G_b$ =

3

Wieviel gewinnt er im Mittel pro Spiel, wenn er stets 1 Euro auf „0“ und 10 Euro auf „Rot“ setzt?

$G_c$ =

4

Der Spieler setzt wie im Bild gezeigt. Auf welche Zahl $Z$ sollte er hoffen? Wie groß wäre dann sein Gewinn?

$Z$ =

$G_d$ =

5

gibt es eine Setzkombination, so dass der mittlere Gewinn positiv ist?

	Ja (Studium beenden, in die nächste Spielbank gehen).
	Nein (das bedeutet: Weitermachen mit LNTwww).

Musterlösung

Solution

1.   Der Spieler verliert jeweils 1 Euro, wenn eine der Zahlen „1“ bis „36“ gezogen wird. Er gewinnt 33 Euro, wenn tatsächlich die Null getroffen wird. Daraus folgt:

$$\it G_a = \rm \frac{36}{37}\cdot (-1\hspace{0.1cm} Euro) + \frac{1}{37}\cdot (33\hspace{0.1cm} Euro) \hspace{0.15cm}\underline {= - 0.081\hspace{0.1cm} Euro\hspace{0.1cm}(Verlust)}.$$

2.  Der Spieler gewinnt und verliert nichts, wenn nicht die Null gezogen wird. Erscheint die Null, so verliert er seinen Einsatz:

$$\it G_b = \rm \frac{1}{37}\cdot (-2\hspace{0.1cm} Euro)\hspace{0.15cm}\underline { = -0.054 \hspace{0.1cm}Euro \hspace{0.1cm}(Verlust)}.$$

3.   Den höchsten Gewinn erzielt er bei Z = „23“. Dann gewinnen vier seiner fünf Chips:

$$\it G_c = \rm \frac{18}{37}\cdot (10 -1) + \frac{1}{37}\cdot (35-10) + \frac{18}{37}\cdot (-10-1)\hspace{0.15cm}\underline { = - 0.297\hspace{0.1cm}Euro}.$$

4.   Den höchsten Gewinn erzielt er bei Z = „23“. Dann gewinnen vier seiner fünf Chips:

$$\it G_d = \rm 10\hspace{0.1cm}Euro\hspace{0.1cm}(da\hspace{0.1cm} Rot ) + 10\hspace{0.1cm}Euro\hspace{0.1cm}(da\hspace{0.1cm} Passe) + 10\hspace{0.1cm}Euro\hspace{0.1cm}(da \hspace{0.1cm} Impair) + $$ $$+\rm 11\hspace{0.1cm}Euro\hspace{0.1cm}(da\hspace{0.1cm}zwischen \hspace{0.1cm}22\hspace{0.1cm} und \hspace{0.1cm}24) - 1 \hspace{0.1cm}Euro\hspace{0.1cm}(da \hspace{0.1cm}nicht \hspace{0.1cm}0) \hspace{0.15cm}\underline {= 40 \hspace{0.1cm}Euro}.$$

Kommt dagegen die Null, so gewinnt er lediglich = 35 – 31 = 4 Euro.

5   Nein, leider nicht. Im statistischen Mittel gewinnt immer die Bank.